Простые формы кристаллов высшей категории

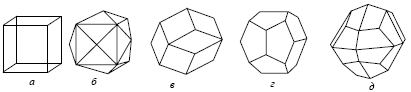
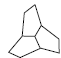
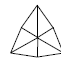
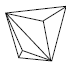
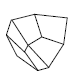
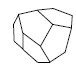
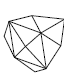
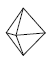
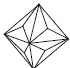
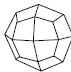
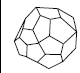
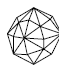
Высшая категория имеет только одну простую форму, сходную с формами низшей и средней категории – тетраэдр. Но при этом тетраэдр кубической сингонии отличается от тетрагонального и ромбического тетраэдра тем, что его грани являются равносторонними треугольниками, тогда как у тетрагонального тетраэдра они являются равнобедренными, а у ромбического – произвольными треугольниками с тремя неравными ребрами.

Все остальные простые формы кубической сингонии новые. К ним относятся: гексаэдр, октаэдр, додекаэдр и производные от них формы (рис. 19).

Гексаэдр представляет собой правильный шестигранник (куб) с квадратной формой грани.

Октаэдр – это простая форма в виде правильного восьмигранника.

Додекаэдр – правильный двенадцатигранник. В зависимости от формы грани могут быть следующие простые формы этого типа: ромбододекаэдры – форма грани в виде ромба; пентагондодекаэдры с формой грани в виде пятиугольника. Правильный двадцатичетырёхгранник называется дидодекаэдром.

При четырёх основных простых формах высшей категории (тетраэдр, гексаэдр, октаэдр и додекаэдр) существуют комбинированные простые формы. Названия таких форм кубической сингонии даны по следующему принципу: первая часть слова (тригон, тетрагон, пентагон) характеризует очертание грани данной формы (тригон = три + гон = треугольник), вторая часть слова (тритетраэдр - триоктаэдр) указывает: а) от какой простой формы данная форма является производной; б) сколько граней данной формы расположено на каждой грани простой формы; в) чему равно число граней данной формы.

Рис. 19. Простые формы кубической сингонии:

Куб (гексаэдр) (а), тетрагексаэдр (б), ромбододекаэдр (в), пентагондодекаэдр (г), дидодекаэдр (д)

 

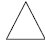
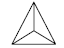
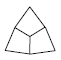
Примеры названий комбинированных простых форм:

– кристалл представляет собой тетраэдр, у которого каждая из четырёх граней состоит из трёх маленьких треугольных граней. Такая форма будет иметь название тригон-три-тетраэдр;

– кристалл представляет собой октаэдр, каждая из восьми граней которого составлена из трёх малых четырёхугольных граней. Такая форма имеет название тетрагон-три-октаэдр.

Если взять за исходные простые формы тетраэдр и октаэдр, то можно получить ряд производных простых форм (рис. 20).

		Форма граней
Исходная форма	Октаэдр
		Тетраэдр	Тригонтритетраэдр	Тетрагонтритетраэдр	Пентагонтритетраэдр	Гексатетраэдр
	Тетраэдр
		Октаэдр	Тригонтриоктаэдр	Тетрагонтриоктаэдр	Пентагонтриоктаэдр	Гексаоктаэдр

Рис. 20. Простые формы кубической сингонии, образованные от

тетраэдра и октаэдра

 

В верхней строке показаны формы граней. Первой изображена грань правильного (кубического) тетраэдра – равносторонний треугольник. Если вместо одной грани появляются три, то фигура называется тритетраэдр, если шесть – гексатетраэдр. Так как тритетраэдров может быть несколько, то перед названием указывается форма каждой из получающихся граней. Грани тритетраэдров могут быть треугольные, четырехугольные и пятиугольные, соответственные фигуры, имеющие такие грани, получают название тригон-тритетраэдр, тетрагон-тритетраэдр и пентагон- тритетраэдр.

Те же самые по форме грани могут быть и у октаэдров (нижняя строка). Их названия получаются таким же образом, как и для тетраэдров.

Соответственно получим следующие 5 простых форм кубической сингонии: октаэдр, тригон-триоктаэдр, тетрагон-триоктаэдр, пентагон-триоктаэдр и гексаоктаэдр.

Общее число граней у всех простых форм легко может быть высчитано, если учитывать их название.

Тетраэдр и октаэдр имеют соответственно 4 и 8 граней. Все тритетраэдры будут иметь по 12 граней, а триоктаэдры – по 24. Гексатетраэдр также имеет 24 грани, а гексаоктаэдр – 48. Это максимальное число граней, которое может иметь простая форма.

Для определения простой формы кристаллов кубической сингонии следует сориентировать кристалл таким образом, чтобы одинаковые группы граней можно было свести к одной из базовых простых форм (тетраэдр, октаэдр, додекаэдр). После этого легко определить название комбинированной формы.