
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Занятие 7. Корреляция и регрессия
Расчетное время – 2 часа. В агрономических исследованиях чаще всего встречаются такие соотношения между переменными, когда каждому значению признака Х соответствует не одно, а множество возможных значений признака У, т.е. их распределение. Такие связи, обнаруживаемые лишь при массовом изучении признаков, в отличии от функциональных (когда каждому значению одной величины соответствует строго определённое значение другой) называются вероятностными, или корреляционными. Корреляционные связи характеризуются двумя основными показателя- ми – теснотой связи и формой связи. Для измерения тесноты и формы связи используют статистические методы, называемые корреляцией и регрессией. Зависимость называется корреляционной, если с увеличением средней величины первого признака увеличивается средняя величина второго, или, наоборот, с увеличением средней величины первого признака второй уменьшается. В первом случае корреляция и регрессия – прямая, или положительная, во втором – обратная, или отрицательная (направление корреляции). По форме корреляция и регрессия может быть линейной и криволинейной. Корреляцию и регрессию называют простой, или парной, если исследуется связь между двумя признаками, и множественной, когда изучается зависимость между тремя и более признаками. Регрессией называют изменение результативного признака У (функции) при определённом изменении одного или нескольких факториальных (аргументов). Связь между функцией и аргументом выражается уравнением регрессии, или корреляционным уравнением. При простой регрессии уравнение кратко обозначается У=f(X) и при множественной У=f (X, Z, V…). Для оценки тесноты (силы) связи используют коэффициенты корреляции и корреляционное отношение. Линейная корреляция – это такая зависимость между двумя признаками Х и У, которая носит линейных характер и выражается уравнением приямой линии У = а+вХ. Это уравнение называется уравнением регрессии У на Х, а соответствующая ему прямая линия – выборочной линией регрессии У на Х. Линейная регрессия – это такая зависимость, когда при любом значении аргумента Х одинаковые приращения его вызывают одинаковые изменения функции У. Когда при одинаковых приращениях аргумента функция имеет неодинаковые изменения, регрессия называется криволинейной.
В агрономии большинство связей криволинейные. Однако некоторые из них близки к линейным и их удобней анализировать как линейные зависимости, вычисляя коэффициент корреляции (r) – числовой показатель простой линейной корреляции, указывающий на тесноту (силу) и направление связи Х с У. Данный показатель рассчитывается по формуле:
Значение коэффициента корреляции лежит в пределах от +1 до -1. Если r = 0,0 – корреляция отсутствует; r £ 0,3 – корреляция слабая; r = 0,3-0,7 – корреляция средняя; 0,7 < r <1,0 – корреляция тесная (сильная); r = 1,0 – корреляция полная (функциональная зависимость). Квадрат коэффициента корреляции (r2) называется коэффициентом детерминации и обозначается dУХ. Он показывает долю (%) тех изменений, которые в данном явлении зависят от изучаемого фактора. Задача 1. Провести анализ зависимости между длинной листьев озимой пшеницы и их площадью (табл. 24). Таблица 24. Вычисление корреляционной зависимости между длиной листа озимой пшеницы (см) и его площадью (см2).
Количество пар (n) = 20.
Корреляционный анализ. Вычисления проводят по формулам: 1. Коэффициент корреляции
2. Стандартная ошибка коєффициента корреляции
3. Критерий достоверности коэффициента корреляции
Теоретическое значение критерия Стьюдента находят по числу степеней свободы νr = n-2 = 20-2 = 18;
t0,95 = 2,1; t0,99 = 2,88. Вывод 1. Так как коэффициент корреляции r = 0,98 (≈ 1), то связь между длиной листа озимой пшеницы и его площадью сильная, почти полная. При этом знак «+» показывает, что коэффициент корреляции положительный, а, следовательно, корреляция прямая.
Вывод 2. В связи с тем, что фактический критерий достоверности коэффициента корреляции равен 20,9, что значительно больше теоретических значений to,95 (2,1) и t0,99 (2,88), поэтому связь между длиной листа озимой пшеницы и его площадью достоверна на наивысших уровнях значимости.
Если количество пар незначительное, тогда оценка достоверности коэффициента корреляции искажается. Р. Фишер предложил оценивать достоверность по критерию tZ, пользуясь формулой tZ = Значения Z находят в приложении 7 для определённого значения коэффициента корреляции r. Например, n = 7, r = 0,69. В этом случае Z = 0,848, а tZ = 0,848 Число степеней свободы νr = n-2 = 7-2 = 5, для которого t0,95 = 2.57, а t0,99 = 4,03. Так как tZ = 1,7, что меньше t0,95 и t0,99, то связь недостоверная. Для оптимизации количества пар (повторностей) при изучении корреляционной связи применяют формулу nОПТ = где t – критерий Стьюдента для νr, которое для приведеного выше примера составляет n-2 = 7-2 = 5. При этом t0,95 = 2,57, a t0,99 = 4,03; Z – показатель, предложенный Р.Фишером, в нашем примере равен 0,848. Оптимальное количество пар определяют по формулам 1) n0,95 = 2,572/0,8482 + 3 = 12,2 ≈ 13 (пар); 2) n0,99 = 4,032/0,8482 + 3 = 25,6 ≈ 26 (пар). Таким образом, для проведения корреляционного анализа на уровне Р0,95 необходимо иметь выборку из 13, а на уровне Р0,99 – из 26 пар. Регрессионный анализ. При сильной и достоверной связи в любом направлении (прямой или обратной) осуществляют регрессионный анализ. 1. Коэффициент регрессии – Ryx. Для нашего примера логично вычислить изменение площади листа озимой пшеницы при изменении его длины на 1 см:
2. Площадь листа (У) при его длине (Х) вычисляют по уравнению регрессии
у = Значения х получают после измерения длины 20-30 листьев пшеницы и определения их средней длины. Например, среднее значение длины листа составляет 21,7 см (10-я пара в табл. 24). Фактическое значение площади листа при этой длине составляет 13,6 см2, а расчетное будет таким: у = 14+1,42 (21,7-21,4)= 14+0,43 = 14,4 см2. Разница между расчётной площадью и фактической составляет 14,4 – 13,6 = 0,8 см2, или х = 0,8·100/13,6 = 5,9%. Таким образом, по уравнению регрессии площадь листа вычислена с удовлетворительной точностью. Умножив площадь одного листа на их количество, получим общую листовую поверхность на одном растении или на определённой площади посева.
Производственный сельскохозяйственный опыт
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 399; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.35.81 (0.013 с.) |
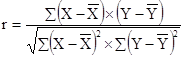 .
.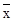

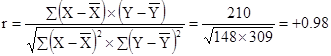 .
. .
.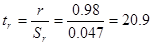 .
.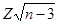
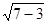 = 1,7.
= 1,7.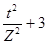 ,
, (см2 на 1 см длины).
(см2 на 1 см длины). + Ryx (х -
+ Ryx (х -  ) = 14+1,42 (х-21,4).
) = 14+1,42 (х-21,4).


