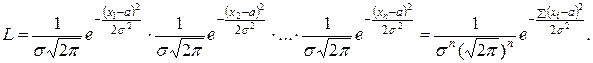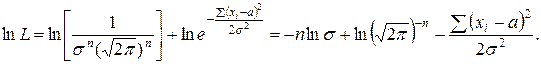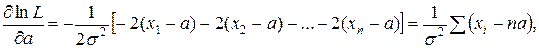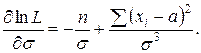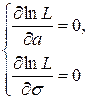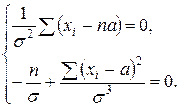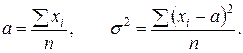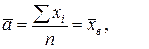Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод максимального правдоподобияСодержание книги
Поиск на нашем сайте Для построения точечных оценок в статистике применяют различные методы: метод максимального правдоподобия, метод моментов, метод наименьших квадратов. Ограничимся первым из них. Пусть X – случайная величина, которая в результате n независимых опытов приняла значения: Введем обозначение:
Функция Идея метода заключается в том, что в качестве точечной оценки параметра a принимается такое значение Оценку Для отыскания максимума функции правдоподобия применяются обычные правила отыскания экстремума функции: Решается уравнение Замечания. 1. Функции L и lnL достигают максимума при одном и том же значении параметра a Поэтому вместо отыскания максимума функции L часто ищут максимум функции lnL – логарифмической функции правдоподобия, что оказывается удобнее. 2. Для непрерывной случайной величины X функцией правдоподобия называется функция параметра a вида:
где Оценка максимального правдоподобия неизвестного параметра распределения непрерывной случайной величины строится так же, как и для дискретной случайной величины. Пример. Найти методом максимального правдоподобия оценки параметров a и
если значения, принятые случайной величиной X в результате n испытаний равны: Так как нормальный закон распределения характеризуется двумя параметрами
Логарифмируя это выражение, получим:
Частные производные от логарифмической функции правдоподобия по a и
Поэтому система уравнений правдоподобия примет вид
или
Решая эту систему, получим:
Следовательно, искомые оценки максимального правдоподобия будут:
|
||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 110; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

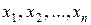 , и пусть закон распределения X известен, но с точностью до некоторого параметра a, от которого он зависит. Требуется найти подходящую точечную оценку
, и пусть закон распределения X известен, но с точностью до некоторого параметра a, от которого он зависит. Требуется найти подходящую точечную оценку 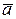 параметра a.
параметра a.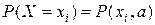 и составим функцию L, равную произведению вероятностей независимых событий
и составим функцию L, равную произведению вероятностей независимых событий 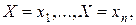 то есть вероятности их совместного осуществления:
то есть вероятности их совместного осуществления: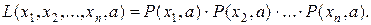
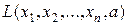 аргумента a (
аргумента a (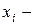 фиксированные числа) называется функцией правдоподобия дискретной случайной величины X.
фиксированные числа) называется функцией правдоподобия дискретной случайной величины X.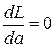 (его называют уравнением правдоподобия), затем вычисляется вторая производная
(его называют уравнением правдоподобия), затем вычисляется вторая производная 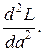 Если она при
Если она при 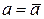 отрицательна, то
отрицательна, то 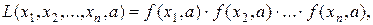
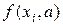 - плотность вероятностей.
- плотность вероятностей.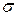 нормального закона распределения:
нормального закона распределения: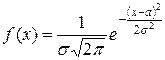 ,
,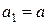 и
и 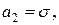 то функция правдоподобия будет функцией двух переменных:
то функция правдоподобия будет функцией двух переменных: