
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценка генеральной средней бесповторной выборкиСодержание книги
Поиск на нашем сайте Пусть, как и выше, Так как выбор каждого отдельного элемента по схеме бесповторной выборки будет влиять на исход последующих выборов, то
Выборочной средней бесповторной выборки называется средняя арифметическая значений Оценка
Можно показать, что дисперсия выборочной средней равна Так как величины
следовательно Оценка Так как объем генеральной совокупности N, как правило, весьма большой, то Замечание. Сопоставляя формулы (7.2) и (7.4) можно заключить, что средние квадратичные отклонения выборочной средней бесповторной выборки всегда меньше аналогичной характеристики повторной выборки того же объема. Следовательно, бесповторная выборка точнее повторной выборки того же объема. Но различие между ними существенно лишь, если объем выборки велик по сравнению с объемом генеральной совокупности N. В противном случае точечные оценки параметров распределения для повторной и бесповторной выборок практически совпадают. 7.4. Определение генеральной дисперсии 7.4.1. Повторная выборка Если в выражениях для дисперсии случайной величины Х заменить математическое ожидание его аналогом в статистике - выборочной средней Величина Если значения признака
или
где Оценка
Можно показать, что
Следовательно, Умножая D *(X) на поправочный множитель или для случая, когда имеются повторяющиеся значения признака
Очевидно, исправленная дисперсия является несмещенной оценкой дисперсии в генеральной совокупности. На практике ею пользуются, если n < 30. При бóльших n, естественно, обе оценки (7.5) и (7.6) отличаются друг от друга очень мало. Оценка Бесповторная выборка Как и для повторной выборки, можно показать, что величина является смещенной оценкой генеральной дисперсии при бесповторной выборке:
Несмещенной оценкой генеральной дисперсии при этом будет исправленная дисперсия Замечание. Дисперсии оценок генеральных средних Рассмотрим примеры определения точечных оценок. Пример. При обработке наружного диаметра 15 карданных валов были получены следующие размеры в мм (см. таблицу 6). Определить несмещенные оценки математического ожидания и среднего квадратического отклонения диаметров, полагая, что обработанные диаметры имеют нормальное распределение. Результаты вычислений представлены в таблице 6. Таблица 6
По данным таблицы находим Пример. Объем генеральной совокупности N = 10000, объем выборки n =1000. В результате измерения интересующего нас признака X получено: Выборка повторная: По формуле (7.3) имеем
где Заменяя неизвестное
следовательно,
Выборка бесповторная. При этом
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 165; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

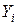 – случайная величина, значение которой совпадает со значением интересующего нас признака
– случайная величина, значение которой совпадает со значением интересующего нас признака  при отборе i - го элемента.
при отборе i - го элемента.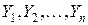 - зависимые случайные величины. Можно показать, что
- зависимые случайные величины. Можно показать, что 
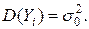
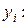
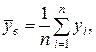
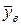 - несмещенная оценка генеральной средней
- несмещенная оценка генеральной средней 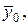 так как
так как
 .
.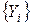 не соблюдаются. Применяя поэтому к выборочной средней неравенство Чебышëва, можно записать
не соблюдаются. Применяя поэтому к выборочной средней неравенство Чебышëва, можно записать
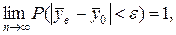 то есть
то есть 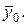
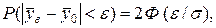 где
где
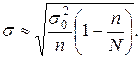 (7.4)
(7.4)
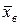 , то получим статистический аналог дисперсии:
, то получим статистический аналог дисперсии: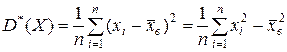 (7.5)
(7.5) называется выборочной дисперсией.
называется выборочной дисперсией.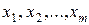 повторяющиеся с частотами соответственно
повторяющиеся с частотами соответственно 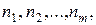 причем
причем  , то выборочная дисперсия вычисляется по формуле
, то выборочная дисперсия вычисляется по формуле
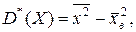
 - средняя квадратов значений признака.
- средняя квадратов значений признака.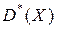 является состоятельной. Действительно, первый член в правой части формулы (7.5) – среднее арифметическое n значений
является состоятельной. Действительно, первый член в правой части формулы (7.5) – среднее арифметическое n значений 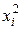 и, следовательно, сходится по вероятности к
и, следовательно, сходится по вероятности к 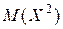 , поэтому
, поэтому .
.
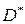 - смещенная оценка параметра
- смещенная оценка параметра 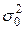 . Ее использование приводит к систематической ошибке в определении генеральной дисперсии, давая заниженное значение
. Ее использование приводит к систематической ошибке в определении генеральной дисперсии, давая заниженное значение  , получим так называемую, исправленную дисперсию
, получим так называемую, исправленную дисперсию 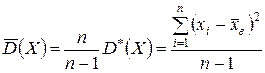 (7.6)
(7.6) 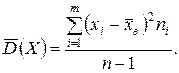
 в общем случае не является эффективной. Однако для наиболее распространенного на практике нормального закона она оказывается асимптотически эффективной (то есть при больших n отношение ее дисперсии к минимально возможной дисперсии неограниченно приближается к единице).
в общем случае не является эффективной. Однако для наиболее распространенного на практике нормального закона она оказывается асимптотически эффективной (то есть при больших n отношение ее дисперсии к минимально возможной дисперсии неограниченно приближается к единице).

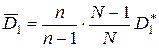 .
.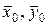 зависят от
зависят от 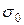 выражается через
выражается через  или
или  ). Но
). Но 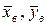 генеральную дисперсию
генеральную дисперсию 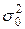 заменяют выборочной (или исправленной) дисперсией.
заменяют выборочной (или исправленной) дисперсией.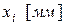

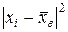
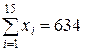


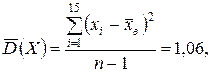
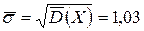 .
.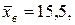
 Найти вероятность того, что среднее значение признака Х отличается от своей оценки на величину
Найти вероятность того, что среднее значение признака Х отличается от своей оценки на величину 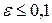 , если выборка повторная; бесповторная.
, если выборка повторная; бесповторная.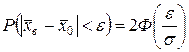 ,
,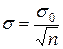 .
.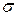 , его оценкой, получим
, его оценкой, получим 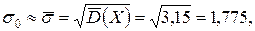
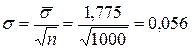 и
и 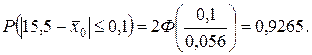
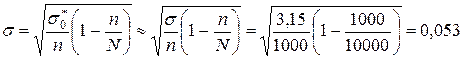 и
и 



