
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрическое определение вероятностиСодержание книги
Поиск на нашем сайте Классическое определение вероятности неприменимо к испытаниям с бесконечным числом элементарных исходов. Задачи, связанные с такими испытаниями, сводятся к случайному бросанию точки в некоторую область. Пусть на плоскости имеется некоторая область F и в ней подобласть f. Предполагая, что вероятность попадания случайной точки в область f не зависит ни от ее формы, ни от ее расположения в области F, а про-порциональна её площади, определим вероятность попадания случайной точки
Здесь mes – мера области: в одномерном случае – длина отрезка, в двумерном – площадь, в трехмерном – объем. Определенная таким образом вероятность называется геометрической вероятностью. Пример. (Задача Бюффона). Плоскость разграфлена параллельными прямыми, отстоящими друг от друга на расстоянии Решение. Пусть Поэтому всевозможные положения иглы изобразятся точками прямо-угольника со сторонами
Предельная линия Алгебра событий Непосредственное вычисление вероятности на основе классиче-ского определения обычно затруднительно, и в теории вероятностей, как правило, применяются косвенные методы, позволяющие по известным вероятностям простых событий определять вероятности сложных событий, с ними связанных. Раздел теории вероятностей, изучающий правила, которым под-чиняются алгебраические операции над событиями, и называется алгеброй событий (ее иногда называют также алгеброй Буля или булевой алгеброй). В основе алгебры событий лежат понятия суммы и произведения событий. Суммой событий называется событие, состоящее в появлении хо-тя бы одного из них. В частности, суммой двух событий A и B будет событие, состоящее в появлении или события A или события B, или обоих вместе. Если события A и B несовместны, то их сумма A+B - событие, состоящее в появлении только одного из них (безразлично какого). Произведением событий называется событие, состоящее в совмест-ном их появлении. Произведение событий A и B обозначается знаком AB. Геометрическая интерпретация суммы и произведения событий показана на так называемой диаграмме Венна. Если событие
Противоположными событиями называются два единственно воз-можных несовместных события, образующие полную группу. Событие, противоположное событию A, обозначается через Очевидно Если известны или могут быть непосредственно (на основе классиче-ского определения) найдены вероятности простых событий, то вероят-ности сложных событий вычисляются c помощью основных теорем тео-рии вероятностей.
|
||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 138; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

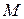 в заданную подобласть как отношение мер областей:
в заданную подобласть как отношение мер областей: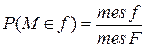 .
.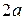 . На плоскость на-удачу бросается игла длиной
. На плоскость на-удачу бросается игла длиной 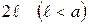 . Найти вероятность того, что игла пересечет какую-нибудь параллель.
. Найти вероятность того, что игла пересечет какую-нибудь параллель.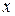 - расстояние от центра иглы до ближайшей па-раллели,
- расстояние от центра иглы до ближайшей па-раллели, 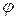 - угол между иглой и параллелью. Величины
- угол между иглой и параллелью. Величины  и
и  полностью определяют положение иглы на плоскости. Очевидно,
полностью определяют положение иглы на плоскости. Очевидно, 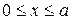 ,
, 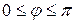 .
.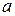 и
и 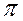 (см. рисунок). Для пересечения иглы с параллелью необходимо, чтобы
(см. рисунок). Для пересечения иглы с параллелью необходимо, чтобы 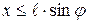 .
.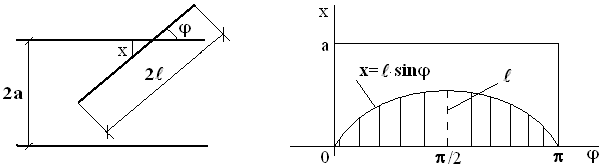
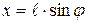 показана на рисунке. Следовательно, благоприятные исходы изобразятся точками заштрихованной области. Искомая вероятность будет равна
показана на рисунке. Следовательно, благоприятные исходы изобразятся точками заштрихованной области. Искомая вероятность будет равна .
. 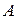 - попадание случайной точки в левую область,
- попадание случайной точки в левую область, 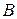 - попадание случайной точки в правую область, то сумма событий
- попадание случайной точки в правую область, то сумма событий 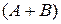 - попадание наудачу брошенной точки в область, ограниченную внешним контуром, произведение событий
- попадание наудачу брошенной точки в область, ограниченную внешним контуром, произведение событий 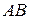 - в зачернённую область:
- в зачернённую область: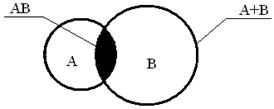
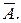
 (U - достоверное событие),
(U - достоверное событие), 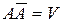 (V - невозможное событие).
(V - невозможное событие).


