
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предельные теоремы теории вероятностейСодержание книги
Поиск на нашем сайте Предельные теоремы делятся на две группы. Теоремы первой группы, объединенные общим названием “ закон больших чисел ”, устанавливают условия, при которых среднее арифметическое случайных величин приближается к некоторым неслучайным (детерминированным) величинам. Теоремы второй группы, объединенные общим названием “цент-ральная предельная теорема”, устанавливают условия, при которых закон распределения суммы случайных величин приближается к нормальному закону. Закон больших чисел Как показывает опыт, при некоторых сравнительно широких условиях сумма достаточно большого числа случайных величин почти утрачивает характер случайной величины и может быть предсказана с большой степенью определенности. Это, так называемое, свойство устойчивости массовых случайных явлений объясняется тем, что случайные отклонения от среднего, неизбежные в каждом отдельном опыте, в массе опытов взаимно погашаются. Именно эта устойчивость средних значений и составляет физическое содержание закона больших чисел. Основными теоремами закона больших чисел являются теоремы Чебышёва и Бернулли. Их доказательство базируется на весьма общей лемме, известной под названием неравенства Чебышëва. Неравенство Чебышëва Вероятность того, что отклонение случайной величины Х от ее мате-матического ожидания
Неравенство Чебышëва дает верхнюю оценку для вероятности отклонения значений случайной величины от своего математического ожидания.
Пусть имеется последовательность независимых случайных величин Говорят, что последовательность
Теорема Чебышëва Если
то есть при Хотя случайные отклонения отдельных величин Xk от своих мате-матических ожиданий могут быть существенны и разного знака (как больше, так и меньше нуля), но в среднем арифметическом (это тоже случайная величина), они взаимно погашаются. Поэтому при достаточно большом n среднее арифметическое значение случайных величин Теорема Бернулли Если в каждом из n независимых испытаний вероятность появления события постоянна, то с вероятностью, близкой к достоверности, можно утверждать, что при неограниченном увеличении числа испытаний относительная частота W появления события сходится по вероятности к его вероятности p:
Следовательно, теоремой Бернулли доказывается свойство устойчи-вости относительной частоты, которое раньше (см. пример с многократным подбрасыванием монеты) рассматривалось как эмпирический факт. Пример. Случайная величина Х имеет нормальное распределение с параметрами a, Решение. Из неравенства Чебышёва следует, что
В рассматриваемом случае
По точной формуле
Пример. Событие А происходит в каждом опыте с вероятностью 0,2. Оценить (с помощью неравенства Чебышёва) вероятность того, что число появлений события А в 1000 независимых опытов будет заключено в пределах от 200 до 300. Решение. Число появлений события А в 1000 независимых испы-таний – случайная величина Х с математическим ожиданием
Наибольшая разность между заданным числом появлений события А и его средним значением М(Х) равна Применяя неравенство Чебышёва, получим Пример. Среднее значение длины детали 50 см, а дисперсия 0,1. Пользуясь неравенством Чебышёва, оценить вероятность того, что случайно взятая деталь окажется по длине не меньше 49,5 см и не больше 50,5 см (в поле допуска). Решение. По условию
Пример. Оценить вероятность того, что
Решение. Находим М(Х) и D (X):
Поэтому
|
||||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 592; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

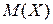 по абсолютной величине меньше малого положительного числа ε, больше или равна
по абсолютной величине меньше малого положительного числа ε, больше или равна 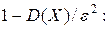
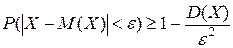 .
.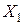 ,
, 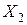 ,
, 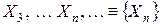 .
.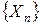 сходится по вероятности к величине
сходится по вероятности к величине 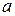 (случайной или неслучайной), если при любом
(случайной или неслучайной), если при любом 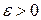 имеет место равенство
имеет место равенство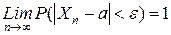 .
.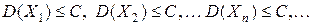 , то каково бы ни было малое положительное число
, то каково бы ни было малое положительное число 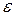 , имеет место равенство
, имеет место равенство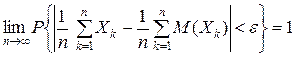 ,
,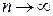 среднее арифметическое случайных величин
среднее арифметическое случайных величин 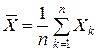 сходится по вероятности к их общему математическому ожиданию.
сходится по вероятности к их общему математическому ожиданию.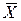 практически уже не случайно и с вероятностью, близкой к достоверности, может приниматься в качестве приближенной оценки математического ожидания
практически уже не случайно и с вероятностью, близкой к достоверности, может приниматься в качестве приближенной оценки математического ожидания 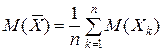 . Этим и объясняется рекомендуемый в практической деятельности способ многократного измерения изучаемой случайной вели-чины с тем, чтобы получить ее значение, близкое к истинному.
. Этим и объясняется рекомендуемый в практической деятельности способ многократного измерения изучаемой случайной вели-чины с тем, чтобы получить ее значение, близкое к истинному.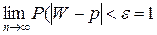 .
.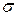 . Оценить по неравенству Чебышёва
. Оценить по неравенству Чебышёва 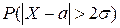 . Сравнить с точным значением этой вероятности.
. Сравнить с точным значением этой вероятности.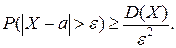
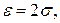
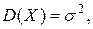 следовательно,
следовательно,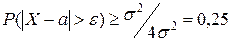 .
.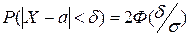 имеем
имеем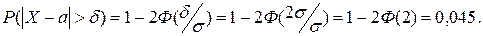
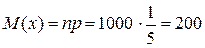 и дисперсией
и дисперсией 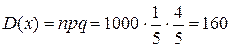 .
.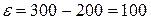 .
.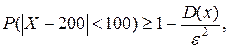
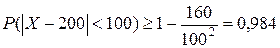 .
.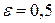 .
.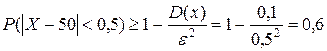 .
.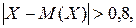 если Х – дискретная случайная величина, имеющая ряд распределения
если Х – дискретная случайная величина, имеющая ряд распределения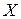
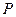
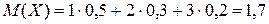 ,
,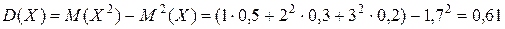 .
.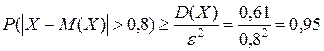 .
.


