Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема о вероятности появления хотя бы одного события.
Если произведено n независимых испытаний, причем вероятности появления событий
где В частности, если события
Пример. В каждом опыте событие А появляется с вероятностью Решение. По условию вероятность появления события хотя бы один раз в n независимых испытаниях Отсюда Непосредственным подбором найдем, что наименьшее допустимое Пример. Из партии, содержащей 100 деталей, последовательно одна за другой извлекаются 5 деталей и подвергаются контролю. Условием непригодности всей партии является появление хотя бы одной брако-ванной детали среди контролируемых. Какова вероятность того, что партия будет принята, если она содержит 5% неисправных деталей? Решение. Пусть A – искомое событие, Очевидно, Применяя теорему умножения вероятностей для зависимых событий, получим Пример. Прибор состоит из 4-х узлов, которые за время работы t могут выходить из строя независимо друг от друга. Надежность (вероят-ность безотказной работы) i -го узла равна Найти вероятности следующих событий: A - все узлы работают без-отказно; B - первый узел отказал, остальные нет; C - один из узлов отказал, остальные нет; D - отказали два узла из 4-х; E - отказало не менее двух узлов; F - отказал хотя бы один узел. Решение. Пусть 1). Событие A произойдет, если одновременно произойдут события Применяя к этому равенству событий теорему умножения вероятностей для независимых событий, получим
2). Событие B произойдет, если одновременно произойдут события
3). Событие C может осуществиться, если откажет первый узел, а ос-тальные три работают или, если откажет второй узел, а работают первый, третий и четвертый и т.д. Следовательно, C - сложное событие, пред-ставляющее собой сумму произведений простых событий:
Применяя к этому равенству сначала теорему сложения вероят-ностей для несовместных событий, а затем к каждому слагаемому теорему умножения вероятностей для независимых событий, получим 4). D - событие, которое может осуществиться шестью различными способами: Поэтому
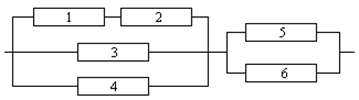
5). Для вычисления вероятности события
Согласно следствию 2 из теоремы сложения вероятностей
6). Для вычисления вероятности события F применим теорему о вероятности появления хотя бы одного события. Тогда получим Пример. Найти вероятность безотказной работы функциональной цепи, состоящей из независимо работающих элементов, если вероятность работы каждого элемента цепи равна p.
Решение. Введем обозначения для всех возможных в данной задаче случайных событий. Пусть A - искомое событие (безотказная работа всей цепи); Тогда
Работа всей цепи
Замечания. 1. Для упрощения расчета систем, содержащих параллельно и после-довательно соединенные элементы, целесообразно при параллельном сое-динении элементов рассматривать предварительно состояние отказа, а при последовательном соединении - состояние работы элементов.
2. Как видно из решения, при увеличении числа параллельно сое-диненных элементов (при резервировании) повышается надежность (веро-ятность безотказной работы) системы, а при увеличении числа последова-тельно соединенных элементов надежность системы понижается. Формула полной вероятности Вероятность события A, которое может наступить лишь при условии появления хотя бы одного из несовместных событий
События Пример. Три автомата штампуют однотипные детали, которые поступают на общий конвейер. Производительности автоматов относятся как 2:3:5. Каждый из автоматов штампует нестандартных деталей в среднем 2,5%; 2% и 1,5% соответственно. Найти вероятность того, что взятая наудачу с конвейера деталь окажется стандартной (событие A). Решение. Пусть
Вероятность того, что деталь стандартна при условии, что она изготовлена первым автоматом
Аналогично. Полная вероятность того, что наудачу взятая с конвейера деталь стандартна, равна
Пример. Имеются 2 урны: в первой Решение. Пусть
Находим вероятности осуществления гипотез:
Условные вероятности осуществления события
По формуле полной вероятности получим
Замечание. При решении задач на применение формулы полной вероятности следует контролировать правильность определения вероят-ностей гипотез. Их сумма всегда должна быть равна единице, так как гипо-тезы образуют полную группу событий, и появление одной из них есть событие достоверное. Формула Бейеса Так как при формулировке теоремы умножения вероятностей безразлично, какое событие считать “первым”, а какое “вторым”, то Отсюда
Подставляя вместо Формула Бейеса позволяет переоценить вероятности гипотез Пример. Детали попадают на проверку стандартности к одному из двух контролёров. Вероятность того, что деталь попадает к первому конт-ролёру равна 0,7; ко второму – 0,3. Вероятность того, что годная деталь будет признана стандартной первым контролёром, равна 0,94; вторым – 0,98. Годная деталь при проверке была признана стандартной (событие А). Найти вероятность того, что ее проверял первый контролёр. Решение. Возможны 2 гипотезы:
По условию задачи Условные вероятности Вероятность того, что признанную стандартной годную деталь про-верял первый контролёр, равна
Формула Бернулли В практических приложениях теории вероятности часто исполь-зуется схема повторяющихся независимых испытаний с двумя возмож-ными исходами в каждом испытании (биномиальная схема или схема Бернулли). Если вероятность появления события A в каждом отдельном ис-пытании постоянна и равна p, то вероятность Замечание. Вероятность того, что событие A в n независимых ис-пытаниях наступит: а) менее k раз; б) не менее k раз; в) более k раз; г) не более k раз находят, применяя теорему сложения вероятностей для несов-местных событий по формулам: а) б) в) г) Пример. Вероятность изготовления стандартной детали при изготов-лении партии однотипных деталей равна 0,9. Что вероятнее: появление не более одной бракованной детали в партии из шести деталей или не более двух бракованных деталей в партии из 12 деталей? Решение. Пусть
По теореме сложения вероятностей для несовместных событий
Изготовление каждой отдельной детали и проверка ее качества могут рассматриваться как отдельное независимое испытание. Поэтому Так как вероятность появления интересующего нас события: брако-ванной детали p = 0,1, то применяя к каждому слагаемому формулу Бер-нулли при
Аналогично вычисляя вероятность события
Следовательно,
|
||||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 91; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.102.124 (0.038 с.) |
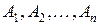 в каждом из них известны и равны соответственно
в каждом из них известны и равны соответственно 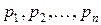 , то вероятность появления хотя бы одного из событий
, то вероятность появления хотя бы одного из событий 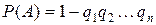 ,
,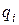 - вероятность противоположного события
- вероятность противоположного события 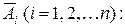
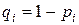 .
.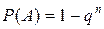 .
.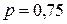 . Сколько опытов необходимо провести, чтобы с вероятностью, не меньшей 0,99 быть уверенным в том, что событие А произойдет хотя бы один раз?
. Сколько опытов необходимо провести, чтобы с вероятностью, не меньшей 0,99 быть уверенным в том, что событие А произойдет хотя бы один раз?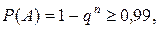 здесь
здесь 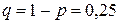 .
.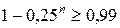 или
или 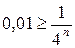 .
.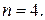
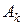 - событие, состоящее в том, что k –ая проверяемая деталь исправна (
- событие, состоящее в том, что k –ая проверяемая деталь исправна (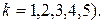
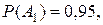
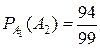 - вероятность того, что вторая про-веряемая деталь годная при условии, что первая деталь тоже годная. Ана-логично
- вероятность того, что вторая про-веряемая деталь годная при условии, что первая деталь тоже годная. Ана-логично 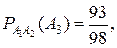

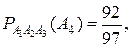
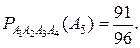
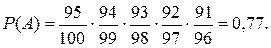
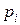 , вероятность отказа
, вероятность отказа 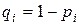
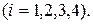
 -работа i -го узла
-работа i -го узла 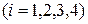 ,
, 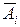 - отказ i -го узла.
- отказ i -го узла.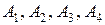 . Следовательно, оно является их произведением:
. Следовательно, оно является их произведением: 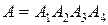 .
.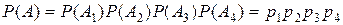 .
.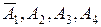 . Следовательно
. Следовательно 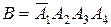 . Вероятность этого события будет равна
. Вероятность этого события будет равна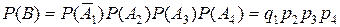 .
.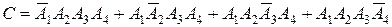 .
.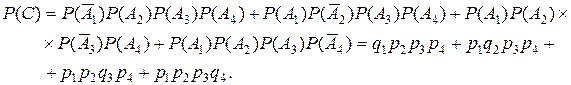
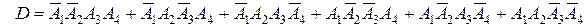 .
.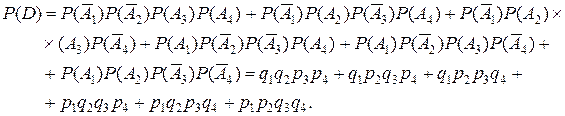
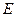 удобно предварительно перейти к противоположному событию
удобно предварительно перейти к противоположному событию 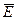 (отказ менее двух узлов). Со-бытие
(отказ менее двух узлов). Со-бытие 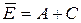 . Поэтому вероятность события
. Поэтому вероятность события 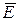 будет равна
будет равна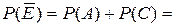
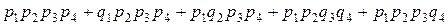 .
.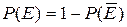 .
.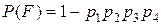 .
.
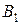 - работа левого контура (элементы 1-4);
- работа левого контура (элементы 1-4); 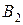 - работа правого контура (элементы 5,6).
- работа правого контура (элементы 5,6).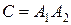 ,
, 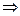
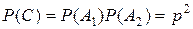 ,
, 
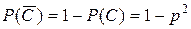 - вероятность отказа верхнего участка цепи (1,2);
- вероятность отказа верхнего участка цепи (1,2);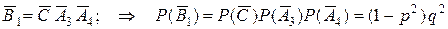 - вероятность отка- за левого контура,
- вероятность отка- за левого контура, 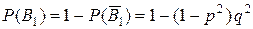 - вероятность работы левого контура,
- вероятность работы левого контура, 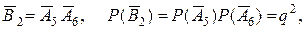
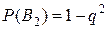 - вероятность работы правого контура.
- вероятность работы правого контура. 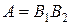 . Поэтому вероятность работы всей цепи равна
. Поэтому вероятность работы всей цепи равна 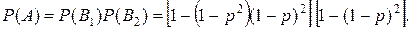
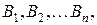 образующих полную группу, равна сумме произведений вероятностей этих событий на соответствующую условную вероятность события A:
образующих полную группу, равна сумме произведений вероятностей этих событий на соответствующую условную вероятность события A: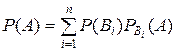 .
.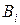 (i = 1, 2,..., n), появление одного из которых предшествует появлению события A, принято называть гипотезами (или априорными гипотезами).
(i = 1, 2,..., n), появление одного из которых предшествует появлению события A, принято называть гипотезами (или априорными гипотезами).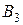 - третьим. Очевид-но, вероятности осуществления гипотез пропорциональны производи-тельности автоматов. Поэтому
- третьим. Очевид-но, вероятности осуществления гипотез пропорциональны производи-тельности автоматов. Поэтому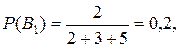
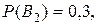
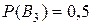 .
.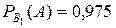 (так как первый автомат производит в среднем 97,5% стандартных деталей). Аналогично,
(так как первый автомат производит в среднем 97,5% стандартных деталей). Аналогично, 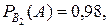
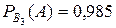 . Следовательно, вероятность того, что наудачу взятая с конвейера деталь стандартна и изготовлена первым автоматом, по теореме умножения вероятностей для зависимых событий равна
. Следовательно, вероятность того, что наудачу взятая с конвейера деталь стандартна и изготовлена первым автоматом, по теореме умножения вероятностей для зависимых событий равна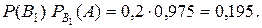
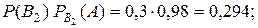
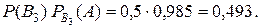
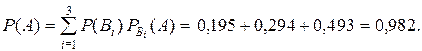
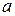 белых шаров и
белых шаров и 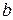 черных; во второй
черных; во второй 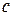 белых и
белых и 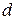 черных шаров. Из первой урны во вторую перекла-дывается один шар, а затем из второй урны в первую перекладывается один шар. После этого из первой урны берут наугад один шар. Найти веро-ятность того, что он будет белым.
черных шаров. Из первой урны во вторую перекла-дывается один шар, а затем из второй урны в первую перекладывается один шар. После этого из первой урны берут наугад один шар. Найти веро-ятность того, что он будет белым.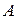 -искомое событие (извлеченный во второй раз из первой урны шар будет белым). Введем следующие гипотезы:
-искомое событие (извлеченный во второй раз из первой урны шар будет белым). Введем следующие гипотезы: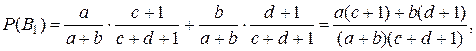
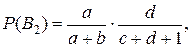
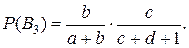
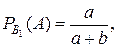
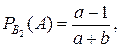
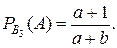
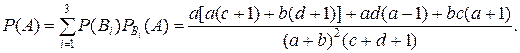
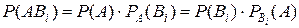 .
.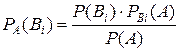 .
.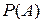 ее значение по формуле полной вероят-ности, получим, так называемую, формулу Бейеса
ее значение по формуле полной вероят-ности, получим, так называемую, формулу Бейеса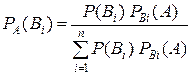
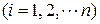 .
.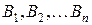 после того, как становится известным результат испытания, в итоге которого появилось событие А, то есть позволяет вычислить веро-ятности гипотез после опыта (так называемых, апостериорных гипотез).
после того, как становится известным результат испытания, в итоге которого появилось событие А, то есть позволяет вычислить веро-ятности гипотез после опыта (так называемых, апостериорных гипотез).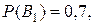
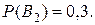
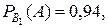
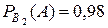 .
. 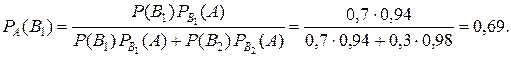
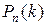 появления события k раз в n независимых испытаниях (следовательно, непоявления события n - k раз с вероятностью q = 1 - p) определяется по формуле Бернулли
появления события k раз в n независимых испытаниях (следовательно, непоявления события n - k раз с вероятностью q = 1 - p) определяется по формуле Бернулли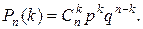
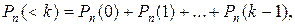
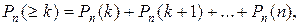
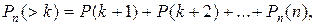
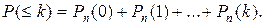
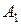 - событие, состоящее в том, что все детали годные (0 бракованных),
- событие, состоящее в том, что все детали годные (0 бракованных), 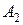 - одна бракованная деталь в малой партии. Тогда
- одна бракованная деталь в малой партии. Тогда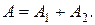
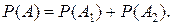
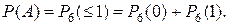
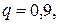
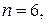 получим
получим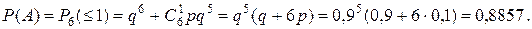
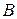 -появления не более двух бракованных деталей в партии из 12-ти деталей, находим
-появления не более двух бракованных деталей в партии из 12-ти деталей, находим