Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Точность оценки. Доверительный интервал
И доверительная вероятность Точечные оценки параметров распределения при выборках малого объема могут существенно отличаться от действительных значений оцениваемых параметров. Поэтому в статистике часто пользуются интервальными оценками(особенно при небольшом числе наблюдений), которые служат для оценки точности и надежности точечных оценок. Интервальной называется оценка, которая определяется двумя числами – концами интервала, в котором заключено неизвестное значение параметра. Пусть для неизвестного параметра θ найдена по данным выборки несмещенная оценка θ *. Чтобы оценить возможную при этом ошибку, назначим некоторую достаточно большую вероятность γ такую, что любое событие, происходящее с вероятностью γ, можно считать практически достоверным. Найдем далее такое ε > 0, при котором с вероятностью γ можно утверждать, что отклонение θ* от θ по модулю не будет превосходить ε, то есть
Величина ε называется точностью оценки. Вероятность γ, с которой осуществляется неравенство Интервал 7.7. Доверительный интервал для оценки Генеральной средней при известном среднем Квадратическом отклонении Пусть для случайной величины X с неизвестной генеральной средней
Воспользуемся тем, что
Учитывая, что вероятность Р задана и равна γ, получим
где число
Следовательно, с надежностью γ можно утверждать, что доверительный интервал Выражение для для бесповторной выборки Замечания. 1. По условию генеральная дисперсия 2. Из формулы для повторной выборки Следовательно, если требуется оценить генеральную среднюю с наперëд заданной точностью ε и надежностью γ, то потребный объем выборки определяется по формулам (7.7), (7.8) соответственно для повторной и бесповторной выборок. Пример. В условиях примера (стр. 106) построить доверительный интервал для математического ожидания, соответствующий доверительный вероятности γ=0,95 в предположении, что выборка является повторной. Так как
По таблице функции Лапласа (см. Приложение 2) находим t при заданном γ=0,95:
Точность оценки Границы доверительного интервала
Следовательно, с надежностью 0,95 можно утверждать, что генеральная средняя Отметим, что повышение надежности оценки γ приводит к возрастанию Φ (t), ε и доверительного интервала, то есть к уменьшению точности определения действительного значения параметра. Пример. В условиях примера (стр. 98) найти с надежностью 0,95 точность γ, с которой выборочная средняя оценивает математическое ожидание диаметров изготовляемых валиков и доверительный интервал для математического ожидания диаметров. Предполагается, что диаметры распределены нормально; выборка повторная.
Для рассматриваемой выборки выборочная средняя
Поэтому
Пример. Определить необходимый объем повторной и бесповторной выборок для определения средней продолжительности горения электрических лампочек, чтобы с вероятностью 0,99 предельная ошибка выборки не превышала 50 часов. Объем всей партии лампочек – 5000 шт. Генеральное среднее квадратическое отклонение принять равным 150 часов. По условию ε = 50,
Итак, выборки должны содержать не менее 60 лампочек. Малая выборка
|
||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 82; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.82.93 (0.007 с.) |
 или
или 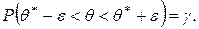
 , называется доверительной вероятностью илинадежностью оценки. Обычно γ задается равным 0,95; 0,99; 0,999.
, называется доверительной вероятностью илинадежностью оценки. Обычно γ задается равным 0,95; 0,99; 0,999.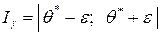 , в котором с надежностью γ заключено неизвестное значение параметра θ, называется доверительным интервалом. Так как длина интервала и положение его на оси абсцисс, определяемое центром θ *, случайны, то говорят, что доверительный интервал I γ накрывает неизвестный параметр θ с заданной надежностью γ.
, в котором с надежностью γ заключено неизвестное значение параметра θ, называется доверительным интервалом. Так как длина интервала и положение его на оси абсцисс, определяемое центром θ *, случайны, то говорят, что доверительный интервал I γ накрывает неизвестный параметр θ с заданной надежностью γ.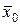 по данным выборки объема n найдена точечная оценка
по данным выборки объема n найдена точечная оценка 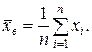 Будем предполагать для простоты, что
Будем предполагать для простоты, что  известно. Для построения доверительного интервала необходимо найти такое
известно. Для построения доверительного интервала необходимо найти такое 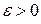 , чтобы выполнялось неравенство
, чтобы выполнялось неравенство .
.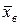 как сумма независимых одинаково распределенных случайных величин Xi при достаточно большом n (а практически уже при n >10-20) согласно теореме Ляпунова имеет закон распределения, близкий к нормальному. Итак, считая, что X распределена по нормальному закону с параметрами
как сумма независимых одинаково распределенных случайных величин Xi при достаточно большом n (а практически уже при n >10-20) согласно теореме Ляпунова имеет закон распределения, близкий к нормальному. Итак, считая, что X распределена по нормальному закону с параметрами  (так как
(так как 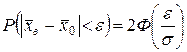 .
.
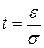 называется квантилем нормального распределения и определяется из условия
называется квантилем нормального распределения и определяется из условия 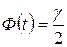 .
. накрывает генеральную среднюю
накрывает генеральную среднюю 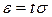 .
.

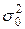 предполагается известной, но если это не так, то для неë используется соответствующая точечная оценка.
предполагается известной, но если это не так, то для неë используется соответствующая точечная оценка.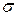 получаем:
получаем: , (7.7) для бесповторной выборки
, (7.7) для бесповторной выборки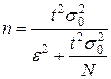 . (7.8)
. (7.8) мм,
мм, 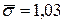 мм, то заменяя
мм, то заменяя 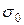 его оценкой
его оценкой 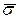 , получим
, получим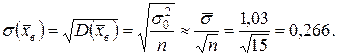
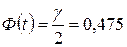 и
и 
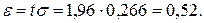

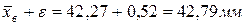 .
.


 ,
, 
 и
и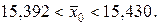

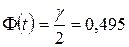 и t =2,58.
и t =2,58.