
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вывод уравнения плоскости по точке и двум направляющим.Содержание книги
Поиск на нашем сайте
Пусть даны точка Возьмём произвольную точку
Тогда определитель равен 0: Вычисляя этот определитель, мы получим в качестве результата некоторое уравнение, содержащее x,y,z. Вывод уравнения прямой в пространстве по точке и направляющему вектору. Пусть дана точка
Пусть произвольная точка
другими словами, их координаты - пропорциональны, т.е.
Это канонические уравнения прямой в пространстве. Теорема о замене. Пусть в пространстве
Если Свойства эквивалентности: 1) 2) если 3) если Лемма. Если Доказательство. Если Тогда
Теорема о замене (Штейница). Пусть в пространстве 2) Из системы (2) можно удалить Доказательство. 1) База индукции. Пусть
Докажем, что Сначала докажем, что
Теперь докажем, что
2) Индукционный шаг. Пусть при
эквивалентная (2). При этом в ней уже заменено Вектор
Здесь хотя бы один из коэффициентов
Значит, какой-то один из векторов (его перенести влево, а
Итак, есть две системы:
где Вектор Итак, возможность замены доказана. Осталось показать, что Следствие. Две эквивалентные системы состоят из одного и того же количества векторов. Если Терминология для бесконечных систем элементов. Пусть дана Пример. Множество
|
||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 121; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.142.42 (0.008 с.) |

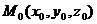 и 2 направляющих вектора
и 2 направляющих вектора 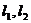 ими однозначно порождается некоторый параллелограмм, а следовательно и плоскость. Обозначим координаты направляющих, например, так:
ими однозначно порождается некоторый параллелограмм, а следовательно и плоскость. Обозначим координаты направляющих, например, так: 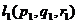 и
и 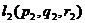 .
.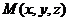 . Если она принадлежит плоскости, то вектор
. Если она принадлежит плоскости, то вектор 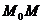 (показан красным цветом) будет лежать в плоскости, то есть тройка векторов
(показан красным цветом) будет лежать в плоскости, то есть тройка векторов 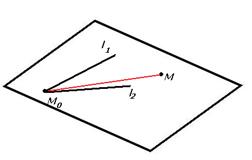
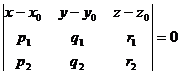
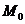 с координатами
с координатами 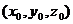 и направляющий вектор
и направляющий вектор 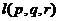 :
:
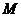 с координатами
с координатами 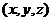 лежит на этой же прямой. Тогда
лежит на этой же прямой. Тогда 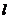 линейно зависимы, то есть ранг следующей матрицы равен 1:
линейно зависимы, то есть ранг следующей матрицы равен 1: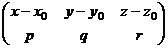
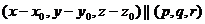 тогда получим:
тогда получим: 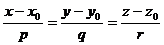 .
.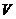 над полем
над полем 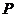 заданы 2 системы векторов:
заданы 2 системы векторов: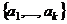 (1) и
(1) и 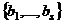 (2). Если каждый вектор системы (1) линейно выражается через систему (2), то будет говорить, что система (1) выражается через (2), обозначается
(2). Если каждый вектор системы (1) линейно выражается через систему (2), то будет говорить, что система (1) выражается через (2), обозначается 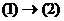 .
. 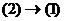 , то системы (1) и (2) называются эквивалентными,
, то системы (1) и (2) называются эквивалентными, 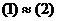 .
. 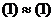 .
. 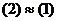 .
.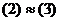 , то
, то 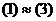 .
.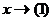 , то
, то 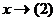 .
. . Но при этом
. Но при этом 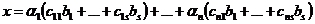 а в таком случае, можно перегруппировать слагаемые и получить
а в таком случае, можно перегруппировать слагаемые и получить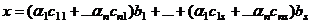 , то есть
, то есть 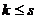 ;
; 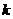 векторов, так, что оставшиеся векторы, вместе с векторами системы (1) составляют новую систему, эквивалентную (2).
векторов, так, что оставшиеся векторы, вместе с векторами системы (1) составляют новую систему, эквивалентную (2).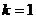 . Система (1) имеет вид
. Система (1) имеет вид 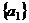 . Тогда во-первых очевидно, что
. Тогда во-первых очевидно, что  , так как (2) содержит хотя бы один вектор.
, так как (2) содержит хотя бы один вектор.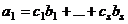 . Пусть в этом равенстве
. Пусть в этом равенстве 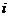 - наименьший индекс, для которого
- наименьший индекс, для которого 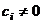 , т.е.
, т.е. 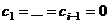 . Тогда можно вектор
. Тогда можно вектор 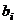 выразить через систему векторов
выразить через систему векторов 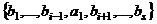 (3):
(3): 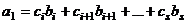
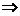
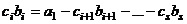
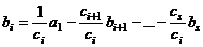 . Итак,
. Итак, 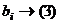 .
. 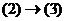 .
.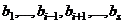 выражаются через (3), так как они принадлежат этой системе (достаточно взять один коэффициент 1, другие 0). А то, что
выражаются через (3), так как они принадлежат этой системе (достаточно взять один коэффициент 1, другие 0). А то, что  (2)
(2)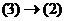 .
.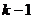 утверждение верно. Тогда существует система
утверждение верно. Тогда существует система (4),
(4),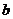 в системе (2).
в системе (2).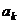 линейно выражается через (2), а значит, и через (4), так как
линейно выражается через (2), а значит, и через (4), так как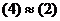 .
. 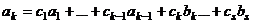 .
. 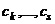 отличен от 0, иначе бы
отличен от 0, иначе бы , что противоречило бы линейной независимости системы (1).
, что противоречило бы линейной независимости системы (1).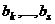 имеет ненулевой коэффициент (пусть для определённости это будет
имеет ненулевой коэффициент (пусть для определённости это будет 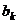 , иначе произведём перенумерацию) а значит, его можно выразить через систему
, иначе произведём перенумерацию) а значит, его можно выразить через систему 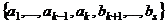 (5)
(5)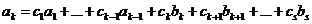
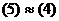 , но при этом было
, но при этом было 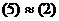 .
. 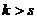 . Тогда на каком-то этапе замены, в системе (2) уже все векторы заменены на векторы из системы (1) (причём проведено
. Тогда на каком-то этапе замены, в системе (2) уже все векторы заменены на векторы из системы (1) (причём проведено 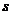 замен). Тогда при замене
замен). Тогда при замене 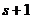 -го вектора мы столкнулись бы с тем, что
-го вектора мы столкнулись бы с тем, что 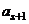 линейно выражается через систему
линейно выражается через систему 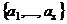 , то есть через подсистему системы (1). Но если какой-то вектор системы (1) линейно выражается через другие векторы этой же системы, это противоречит линейной независимости системы (1), которая по условию теоремы выполняется.
, то есть через подсистему системы (1). Но если какой-то вектор системы (1) линейно выражается через другие векторы этой же системы, это противоречит линейной независимости системы (1), которая по условию теоремы выполняется.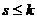 одновременно, а значит,
одновременно, а значит, 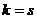 .
. 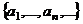 (1) бесконечная система элементов линейного пространства
(1) бесконечная система элементов линейного пространства 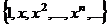 ЛНС. Любая конечная подсистема ЛНС.
ЛНС. Любая конечная подсистема ЛНС.


