
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритм ортогонализации Грама-Шмидта ⇐ ПредыдущаяСтр 10 из 10
Пусть дана не ортогональная система векторов
Таким образом, Далее, рассмотрим вектор
Тогда Аналогично Итак,
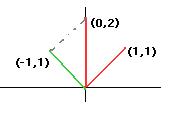
Пример. Ортогонализовать систему векторов (1,1), (0,2).
Лекция 14. 26.12.2020.
Ортогональные матрицы. Пусть новый базис также ортонормированный, тогда матрица перехода обладает следующими свойствами: 1) сумма квадратов всех элементов любого столбца равна 1.
2) скалярное произведение двух различных векторов-столбцов = 0.
Такая матрица называется ортогональной матрицей. Лемма. Если (Объём параллелепипеда, построенного на ортонормированной системе, равен 1). Теорема. Если Доказательство. Умножим
Строка в первой матрице, это бывший столбец (до транспонирования). Таким образом, умножая Тогда
Примером такой матрицы является матрица оператора поворота:
Ещё примеры ортогональных матриц.
Аффинное пространство. Пусть Получается, что заданы отображения По точке и вектору можно построить 2-ю точку, а по 2 точкам вектор. Если выполняются следующие условия: 1) 2) 3) то построенная таким образом структура называется аффинным пространством. Для любых точек 2 типа линейных комбинаций. Барицентрическая комбинация (сумма коэффициентов равна 1). Результат – точка из Множество точек P = kM+(1-k)N (3-я точка на прямой, MN) – аффинно-зависима. Сбалансированная комбинация (сумма коэффициентов равна 0). Результат – вектор Метрическое пространство Пусть 1) 2) 3) То множество Если пространство евклидово, то можно превратить в метрическое:
Элементы векторной алгебры. Скалярное, векторное, смешанное произведение. Скалярное произведение А сейчас мы научимся с помощью матриц и определителей находить общий перпендикуляр для пары векторов. Векторное произведение. Определение. Вектор 2) Векторы 3)
Таблица свойств скалярного и векторного произведений: сходство и различия.
Метод нахождения векторного произведения с помощью определителя: Можно записать в 1-ю и 2-ю строку исходные два вектора, в третьей строке добавить произвольные обозначения осей
Миноры порядка 2 будут координатами Доказательство. 1) Получающийся таким образом вектор ортогонален двум исходным: Если скалярно умножить на
Если скалярно умножить на
Докажем также тот факт, что Квадрат модуля векторного произведения равен сумме квадратов миноров координат такого вектора: То есть величине
В то же время
Сократив то, что выделено в больших скобках, получаем одно и то же выражение. - - - Перерыв - - - Пример. Найти векторное произведение векторов (1,1,1) и (1,2,3)
Также можно проверить, что он действительно перпендикулярен исходным векторам (скалярно умножить на 1-й или на 2-й вектор, получим 0). Примечание. Определитель можно вычислять либо разложением по 3-й строке, либо ранее известными методами, в том числе добавить копии двух первых столбцов справа.
Пример без координат (по свойствам). Векторы a,b выражены через p,r: Решение. =
Смешанное произведение. Определяется так: Этот объект корректно определён и существует: векторное произведение первой пары есть какой-то вектор, и его можно скалярно умножить на ещё один, третий вектор, в итоге получится константа. Смешанное произведение вычисляется с помощью определителя так: Обоснование: Если рассмотреть разложение этого определителя по третьей строке, то получится Геометрический смысл: объём параллелепипеда, образованного тремя векторами.
|
||||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 444; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.76.0 (0.052 с.) |
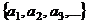 . Первый вектор возьмём из старой системы без изменения
. Первый вектор возьмём из старой системы без изменения  . Теперь мы должны найти второй вектор
. Теперь мы должны найти второй вектор  , так чтобы он был ортогонален
, так чтобы он был ортогонален 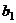 . К вектору
. К вектору 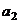 нужно прибавить
нужно прибавить 
 , причём
, причём 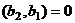 . Тогда
. Тогда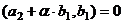 то есть
то есть 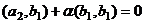 , тогда
, тогда 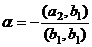 .
. .
.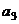 , он также изначально может быть не ортогонален векторам
, он также изначально может быть не ортогонален векторам 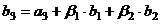 , причём так, чтобы было выполнено
, причём так, чтобы было выполнено  и
и  .
.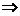
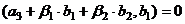
 , причём
, причём 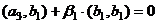
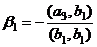 .
.

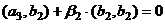
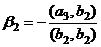 .
.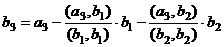 . Теперь все 3 вектора
. Теперь все 3 вектора  ортогональны между собой. Аналогично этот процесс можно продолжить и для n векторов.
ортогональны между собой. Аналогично этот процесс можно продолжить и для n векторов.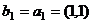 ,
, 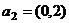 .
.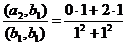 =
= 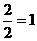 .
. 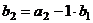 =
=  =
= 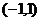
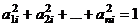
 .
.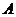 ортогональная матрица, то
ортогональная матрица, то  .
. 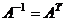 .
.

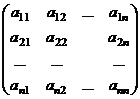 =
= 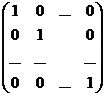
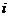 -ю строку на
-ю строку на 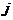 -й столбец, то это то же самое, что скалярно умножить друг на друга
-й столбец, то это то же самое, что скалярно умножить друг на друга  , а значит, транспонированная матрица это и есть обратная, что и требовалось доказать.
, а значит, транспонированная матрица это и есть обратная, что и требовалось доказать. 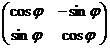 , здесь можно устно проверить, что сумма квадратов элементов каждого столбца равна 1 (по основному тригонометрическому тождеству), а скалярное произведение 1-го и 2-го столбцов 0. Чтобы найти обратную к ней матрицу, достаточно лишь транспонировать её.
, здесь можно устно проверить, что сумма квадратов элементов каждого столбца равна 1 (по основному тригонометрическому тождеству), а скалярное произведение 1-го и 2-го столбцов 0. Чтобы найти обратную к ней матрицу, достаточно лишь транспонировать её.  ,
, 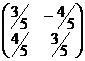 .
. 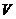 - линейное пространство,
- линейное пространство, 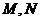 можно поставить в соответствие элемент
можно поставить в соответствие элемент 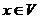 . Упорядоченную пару точек будем называть вектором, обозначать
. Упорядоченную пару точек будем называть вектором, обозначать  .
.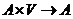 ,
,  .
. существует единственный
существует единственный 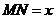 .
. 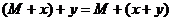
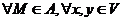 .
.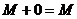
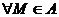 .
.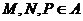 имеет место равенство
имеет место равенство  .
.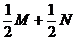 , середина отрезка.
, середина отрезка.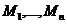 наз. аффинно-независимым, если никакую из них нельзя представить в виде барицентрической комбинации остальных.
наз. аффинно-независимым, если никакую из них нельзя представить в виде барицентрической комбинации остальных.  .
.  поставлено в соответствие некоторое число
поставлено в соответствие некоторое число  , называемое расстоянием между точками и удовлетворяющее аксиомам:
, называемое расстоянием между точками и удовлетворяющее аксиомам: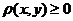 , причём из
, причём из 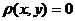 следует
следует 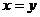 ,
,
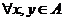 ,
,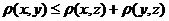
 . (аксиома треугольника).
. (аксиома треугольника).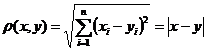 .
. .
. называется векторным произведением векторов
называется векторным произведением векторов  , обозначается
, обозначается 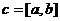 , если выполнены 3 условия: 1)
, если выполнены 3 условия: 1) 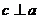 ,
, 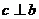 .
. 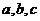 образуют правоориентированную тройку, то есть с конца вектора
образуют правоориентированную тройку, то есть с конца вектора 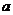 к
к 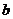 виден против часовой стрелки.
виден против часовой стрелки. параллелограмма, образованного парой векторов
параллелограмма, образованного парой векторов 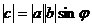 .
.
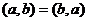
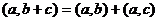

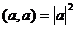

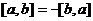
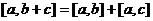
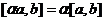
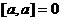

 , и вычислить этот определитель.
, и вычислить этот определитель.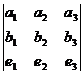 =
= 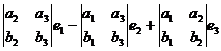 .
. нового вектора, который является векторным произведением.
нового вектора, который является векторным произведением. =
= 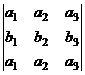 = 0.
= 0. =
= 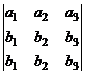 = 0.
= 0.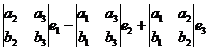
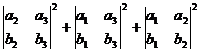 =
=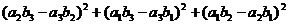 =
=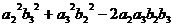 +
+ 
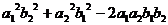 .
.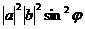 =
= 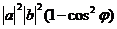 =
= 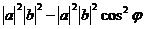 =
= 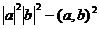 =
=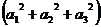
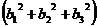
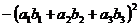 =
=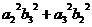 +
+  +
+  +
+ 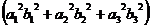
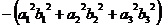
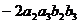

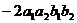 .
.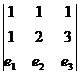 =
= 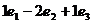 =
= 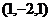 . Ответ (1,-2,1).
. Ответ (1,-2,1).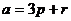 ,
, 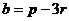 .
. 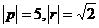 , угол между ними 45 градусов. Найти | [a,b] |.
, угол между ними 45 градусов. Найти | [a,b] |. 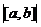 =
= 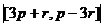 =
= 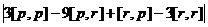
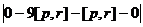 =
=  =
= 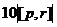 . Модуль векторного произведения
. Модуль векторного произведения 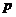 и
и 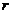 это площадь параллелограмма, где эти векторы являются сторонами, поэтому далее можно продолжить так:
это площадь параллелограмма, где эти векторы являются сторонами, поэтому далее можно продолжить так: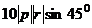 =
= 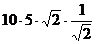 = 50. Ответ. 50.
= 50. Ответ. 50.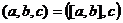 .
.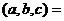
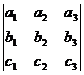 .
.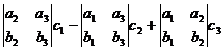 , то есть 1-я координата векторного произведения
, то есть 1-я координата векторного произведения  умножается на 1-ю координату вектора
умножается на 1-ю координату вектора 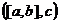 .
.


