
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема 4 (о размерности пространства решений).
Пусть дана линейная однородная система с Доказательство. 1) Если ранг основной матрицы равен Существует такая система решений:
...
Данная система линейно независима, так как объединяя их в матрицу, увидим, что в её последних 2) Докажем, что любое другое решение будет их линейной комбинацией. Рассмотрим последние Пусть Линейная комбинация решений:
Но на последних n-r местах она содержит 0, а числа, отличные от 0 на первых r местах. Но тогда первые r столбцов образовали бы ЛЗС – было бы противоречие. Тогда единственная возможность: Тогда Таким образом, существует не меньше, но и не больше, чем
Определение. Данная система, состоящая из Пример. (
Решение. Если преобразовывать расширенную матрицу, то получим:
Видим, что справа всё равно как был, так и остаётся столбец из нулей, так что в будущем для однородных систем можно использовать только основную матрицу, ведь расширенная не несёт никакой новой информации, всё равно там справа нулевой столбец, и он не меняется при преобразованиях строк. Итак, получили систему Из 2-го:
Общее решение системы:
Также записывается в виде вектора: Частные решения: То есть все тройки чисел будут пропорциональны какой-то одной. ФСР (фундаментальная система решений). ФСР состоит из одного вектора Ответ. Общее решение Пример. (
Базисный минор порядка 2 можно найти в левом углу, тогда считаем, что 3-я и 4-я переменная - свободные. Перенесём их через знак равенства.
Общее решение: { Если поочерёдно присвоить значение 1 каждой из свободных переменных (а другая в это время 0) то получим гарантированно 2 линейно-независимых вектора, они не пропорциональны, так как 1 на разных местах.
Эти 2 вектора { Например, их сумма Примечание. При решении системы в прошлой задаче, со следующей стадии:
* Для системы с квадратной матрицей справа были только числа, для системы с прямоугольной матрицей к ним добавляются свободные переменные, и там будут выражения типа
|
|||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 120; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.30.253 (0.009 с.) |
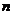 неизвестными, ранг основной матрицы равен
неизвестными, ранг основной матрицы равен 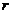 . Тогда существует
. Тогда существует  линейно-независимых решений однородной системы, всякое другое решение есть их линейная комбинация.
линейно-независимых решений однородной системы, всякое другое решение есть их линейная комбинация.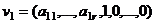
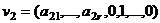
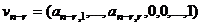
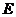 , т.е. заведомо ненулевой, равный 1.
, т.е. заведомо ненулевой, равный 1. 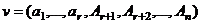 - решение однородной системы.
- решение однородной системы.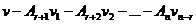 тоже является решением.
тоже является решением.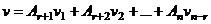 , то есть новое решение можно представить в виде такой линейной комбинации ранее найденных
, то есть новое решение можно представить в виде такой линейной комбинации ранее найденных 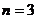 ,
, 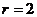 ). Решить однородную систему:
). Решить однородную систему: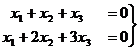
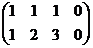


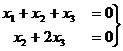 базисный минор можно заметить в первых двух столбцах, так что
базисный минор можно заметить в первых двух столбцах, так что 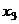 свободная переменная, переносим её вправо:
свободная переменная, переносим её вправо: 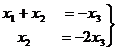 . Теперь последовательно выражаем через свободную переменную две базисные переменные.
. Теперь последовательно выражаем через свободную переменную две базисные переменные.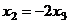 , а подставляя в 1-е, получим
, а подставляя в 1-е, получим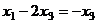 , т.е.
, т.е. 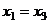 .
.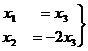 .
. 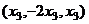 .
.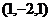 ,
, 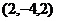 ,
, 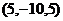 , и т.д.
, и т.д.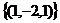 .
.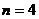 ,
, 
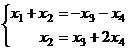 .
. 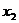 уже фактически выражено:
уже фактически выражено: 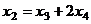 , подставим это в первое уравнение, чтобы выразить
, подставим это в первое уравнение, чтобы выразить 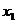 .
.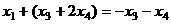
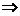
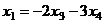 .
.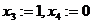
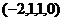
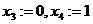
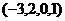 .
.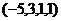 также является решением системы.
также является решением системы.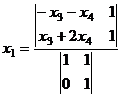 =
= 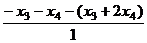
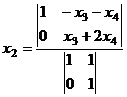 =
= 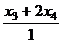
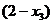 . А для однородной системы справа констант нет (они 0), но туда перенесены свободные переменные. Т.е. решение методом Гаусса во всех этих 3 параграфах выполняется похожим образом, только справа разные типы объектов.
. А для однородной системы справа констант нет (они 0), но туда перенесены свободные переменные. Т.е. решение методом Гаусса во всех этих 3 параграфах выполняется похожим образом, только справа разные типы объектов.


