
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Взаимосвязь координат в разных базисах.Содержание книги
Поиск на нашем сайте
Координаты относительно нового базиса: практические методы их нахождения. (С помощью системы линейных уравнений и с помощью обратной матрицы).
Пусть
Это приводит к системе уравнений:
с основной невырожденной квадратной матрицей, так как столбцы линейно независимы, ведь их составляют векторы базиса. Далее либо решается система (методом Гаусса), либо матричным методом: Матрица Пример. Доказать, что векторы
Система линейно независима, вспомнить: Следствие. Всякая линейно-независимая система из n векторов n-мерного пространства является базисом. Итак, данная система векторов является базисом.
Выразим вектор через этот базис:
Для того, чтобы найти координаты
Она уже приведена к ступенчатому виду (выше побочной диагонали коэффициенты, ниже нули). Из первого, Итак, новые координаты
Пример. Доказать, что множество многочленов Решение. Мы можем просто построить матрицу перехода от одного базиса к другому и доказать её невырожденность. Старый базис
Строим матрицу: Матрица верхне-треугольная, её определитель равен 1, она невырожденная. Например, при
Чтобы найти разложение по новому базису, достаточно решить систему уравнений, причём её основная матрица уже в треугольной форме, т.е. прямой шаг метода Гаусса не потребуется. Пусть
Проверка. Пример. В 4-мерном линейном пространстве матриц порядка 2 базисом является множество матриц: A = Является ли базисом множество матриц:
Построим матрицу перехода.
M1 = 1A+1B+0C+0D координаты (1,1,0,0). Матрица перехода: Вычислим её определитель, разложив по 1-й строке.
первый из миноров разложим по 1-й строке, а второй по 1-му столбцу. Тогда получим Эта система линейно зависима, базисом не является. И действительно, один из элементов можно выразить через другие:
- - - Перерыв - - - Теорема 3 (о продолжении базиса). Для каждой линейно независимой системы векторов
Доказательство. Система Применим теорему о замене. Это возможно, т.к. (1) ЛНС и (1) выражается через (2). В (2) заменим Она ЛНС, так как эквивалентна базису (2). ЛНС из n векторов также является базисом.
|
||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 190; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.237.203 (0.008 с.) |

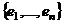 - «старый» базис, в качестве которого, как правило, рассматриваем декартов базис, напр.
- «старый» базис, в качестве которого, как правило, рассматриваем декартов базис, напр. 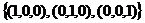 . Пусть задан новый базис из n векторов
. Пусть задан новый базис из n векторов 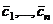 . Нужно найти координаты вектора
. Нужно найти координаты вектора 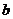 относительно нового базиса.
относительно нового базиса.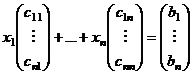
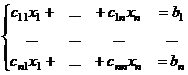
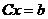
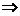
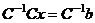
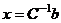 .
. 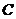 , содержащая координаты векторов нового базиса, выраженные относительно старого (по столбцам), называется матрицей перехода от старого базиса к новому. По построению, она невырождена,
, содержащая координаты векторов нового базиса, выраженные относительно старого (по столбцам), называется матрицей перехода от старого базиса к новому. По построению, она невырождена, 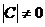 .
. 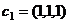 ,
, 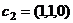 ,
, 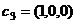 образуют базис 3-мерного пространства, и найти координаты вектора
образуют базис 3-мерного пространства, и найти координаты вектора 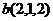 относительно этого базиса.
относительно этого базиса.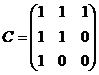 ,
, 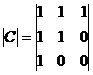 =
= 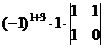 =
= 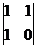 = -1.
= -1. 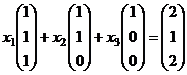
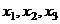 , нужно решить систему уравнений.
, нужно решить систему уравнений.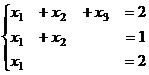
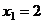
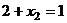
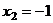 ,
, 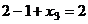
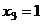 .
.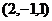 . Проверка. Действительно,
. Проверка. Действительно,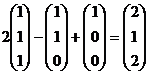
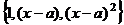 образует базис в линейном пространстве многочленов степени не выше 2. Построить матрицу перехода.
образует базис в линейном пространстве многочленов степени не выше 2. Построить матрицу перехода.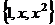 . Найдём координаты этих элементов относительно старого базиса. e1 = 1 e2 = x …
. Найдём координаты этих элементов относительно старого базиса. e1 = 1 e2 = x …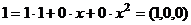
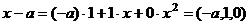
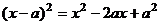 =
= 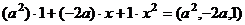
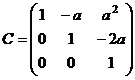 .
.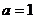 для
для 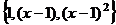 имеет вид:
имеет вид: 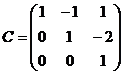
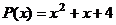 . Разложить по основанию
. Разложить по основанию 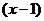 .
.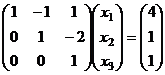
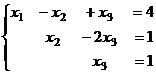
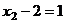
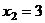 , из 1-го:
, из 1-го: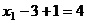
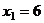 . Итак,
. Итак, 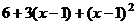 =
= 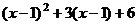 .
. 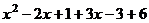 =
= 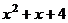 .
. , B =
, B = 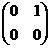 , C =
, C = 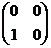 , D =
, D = 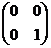 .
.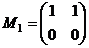 ,
, 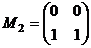 ,
, 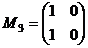 ,
, 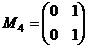 .
.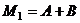 ,
, 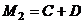 ,
, 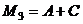 ,
, 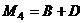 .
. .
.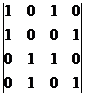 =
= 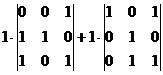
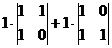 =
= 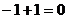 .
.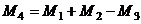 .
. 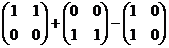 =
= 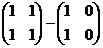 =
= 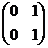 .
.  конечномерного пространства
конечномерного пространства 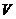 размерности n можно найти такие векторы
размерности n можно найти такие векторы 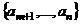 , что система
, что система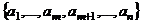 будет базисом пространства
будет базисом пространства 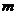 векторов на векторы
векторов на векторы 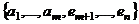 ,
, 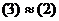 .
. 


