
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Однородные системы линейных уравнений.Стр 1 из 10Следующая ⇒
Лекция 9. 07.12.2020. Однородные системы линейных уравнений. Если в каждом уравнении правая часть
Расширенная матрица содержит столбец, состоящий только из 0, то есть ранг расширенной матриц точно не больше, чем ранг основной! По теореме Кронекера-Капелли получается, что однородная система всегда совместна, то есть существует хотя бы одно решение. Заметим, что при подстановке всех 0 вместо неизвестных, Нетривиальные решения есть, например:
Любое (С,С) для Здесь ранг равен 1, и 2-я переменная свободная.
Если решать методом Гаусса, то получим
Теорема 1. 1) Система линейных однородных уравнений имеет нетривиальные решения 2) Система линейных однородных уравнений с квадратной основной матрицей Доказательство. Система имеет решение, отличное от нуля Итак, однородная система с квадратной основной матрицей имеет нетривиальные решения тогда и только тогда, когда основная матрица вырожденная.
Следствия из теоремы о наложении решений: Теорема 2. Линейная комбинация решений однородной системы тоже является решением (множество решений образует линейное пространство).
Доказательство. Дано
Теорема 3. Сумма решений неоднородной и соответствующей однородной системы есть решение неоднородной системы. Доказательство. Пусть
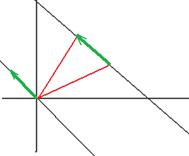
Следствие. Разность двух различных частных решений неоднородной системы есть решение соответствующей однородной системы. Геометрический смысл. Если взять разность двух радиус-векторов, проведённых к точкам какой-либо прямой, не проходящей через начало координат, получится вектор, лежащий на параллельной прямой, проходящей через начало координат.
Доказательство. 1) Если ранг основной матрицы равен Существует такая система решений:
...
Данная система линейно независима, так как объединяя их в матрицу, увидим, что в её последних 2) Докажем, что любое другое решение будет их линейной комбинацией. Рассмотрим последние Пусть Линейная комбинация решений:
Но на последних n-r местах она содержит 0, а числа, отличные от 0 на первых r местах. Но тогда первые r столбцов образовали бы ЛЗС – было бы противоречие. Тогда единственная возможность: Тогда Таким образом, существует не меньше, но и не больше, чем
Определение. Данная система, состоящая из
Пример. (
Решение. Если преобразовывать расширенную матрицу, то получим:
Видим, что справа всё равно как был, так и остаётся столбец из нулей, так что в будущем для однородных систем можно использовать только основную матрицу, ведь расширенная не несёт никакой новой информации, всё равно там справа нулевой столбец, и он не меняется при преобразованиях строк. Итак, получили систему Из 2-го:
Общее решение системы: Также записывается в виде вектора: Частные решения: То есть все тройки чисел будут пропорциональны какой-то одной. ФСР (фундаментальная система решений). ФСР состоит из одного вектора Ответ. Общее решение Пример. (
Базисный минор порядка 2 можно найти в левом углу, тогда считаем, что 3-я и 4-я переменная - свободные. Перенесём их через знак равенства.
Общее решение: { Если поочерёдно присвоить значение 1 каждой из свободных переменных (а другая в это время 0) то получим гарантированно 2 линейно-независимых вектора, они не пропорциональны, так как 1 на разных местах.
Эти 2 вектора { Например, их сумма Примечание. При решении системы в прошлой задаче, со следующей стадии:
* Для системы с квадратной матрицей справа были только числа, для системы с прямоугольной матрицей к ним добавляются свободные переменные, и там будут выражения типа
Лекция 10. 12.12.2020. Теорема о замене. Пусть в пространстве
Если Свойства эквивалентности: 1) 2) если 3) если Лемма. Если Доказательство. Если Тогда
Теорема о замене (Штейница). Пусть в пространстве 2) Из системы (2) можно удалить Доказательство. 1) База индукции. Пусть
Докажем, что Сначала докажем, что
Теперь докажем, что
2) Индукционный шаг. Пусть при
эквивалентная (2). При этом в ней уже заменено Вектор
Здесь хотя бы один из коэффициентов
Значит, какой-то один из векторов (его перенести влево, а
Итак, есть две системы:
где Вектор Итак, возможность замены доказана. Осталось показать, что Следствие. Две эквивалентные системы состоят из одного и того же количества векторов. Если Терминология для бесконечных систем элементов. Пусть дана
Пример. Множество Доказательство. Пусть Если (2) базис, значит, любой вектор из системы (1) можно выразить через него, т.е. Определение. Количество векторов в любом базисе конечномерного пространства
Если пространство n-мерно, то всякая система, состоящая из В плоскости любые 3 вектора образуют ЛЗС, в пространстве 4 вектора, на прямой любые 2 вектора.
Лекция 11. 14.1 2.2020. Теорема 2 (о выражении векторов через базис). Всякий вектор конечномерного линейного пространства линейно выражается через любой базис этого пространства, притом единственным образом. Доказательство. Пусть
Итак, произвольный вектор Единственность. Пусть существуют 2 разных выражения через базис:
Составим разность: Если хоть какие-то коэффициенты были бы отличны, то система Следствие. Всякая линейно-независимая система из n векторов n-мерного пространства является базисом. В плоскости любые 2 неколлинеарных вектора, в пространстве любые 3 некомпланарных вектора образуют базис.
Определение. Коэффициенты линейной комбинации, с помощью которых вектор представлен в виде комбинации векторов базиса, называются координатами этого вектора относительного данного базиса. Доказательство. Необходимость. Пусть Тогда
Достаточность. Пусть Построим изоморфизм так: если
Сохранение операций: 1)
2)
Лекция 12. 19.12.2020. Подпространства. Определение. Пусть Непустое подмножество его элементов, Тривиальные подпространства: 0 и Обозначение:
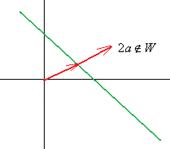
Вовсе не любое подмножество является подпространством. Например, если рассматривать все радиус-векторы, концы которых лежат на прямой, не проходящей через начало координат, то не получается подпространство. Сумма векторов (находится по правилу параллелограмма) оказывается не на этой прямой, впрочем, даже .
Теорема 1. (Критерий подпространства). Пусть Доказательство. Необходимость: если Достаточность. Пусть выполнено: 1) Из 1) следует, что Из 2) следует, что операция внешнего умножения порождает элемент снова из
Теорема 2. Пусть Если Доказательство. 1) Обозначим 2) Допустим,
Определение. Линейной оболочкой системы векторов По критерию подпространства, линейная оболочка является подпространством. Это подпространство, порождённое системой Если эти векторы образуют ЛНС, то Следствие. Если Действительно, Доказательство. 1) Если
2) Если В таком случае Если
Теорема 4. О размерности суммы подпространств. Пусть Доказательство. Пусть Выберем базис
Аналогично, все векторы
Есть 3 системы:
Докажем, что система 1) Докажем, что она ЛНС. Предположим, что она ЛЗС, т.е.
где вектор
|
|||||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 527; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.191.22 (0.148 с.) |
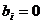 , такая система называется однородной.
, такая система называется однородной.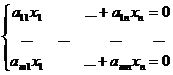
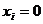 , все равенства автоматически выполняются, т.е. нулевое решение для такой системы всегда существует. Оно называется тривиальным решением. Тривиальное решение может быть не единственным, возможно, есть ещё какие-то наборы чисел, которые можно подставить в систему. Основной задачей для однородных систем как раз и является поиск ненулевых решений.
, все равенства автоматически выполняются, т.е. нулевое решение для такой системы всегда существует. Оно называется тривиальным решением. Тривиальное решение может быть не единственным, возможно, есть ещё какие-то наборы чисел, которые можно подставить в систему. Основной задачей для однородных систем как раз и является поиск ненулевых решений.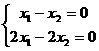 решения (1,1), (2,2), и т.д.
решения (1,1), (2,2), и т.д.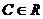 есть решение.
есть решение. А здесь ранг основной матрицы равен 2.
А здесь ранг основной матрицы равен 2. 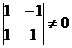 , базисный минор фактически заполняет всю основную матрицу, до правого края, в этом случае нет свободных переменных. Решение только тривиальное.
, базисный минор фактически заполняет всю основную матрицу, до правого края, в этом случае нет свободных переменных. Решение только тривиальное.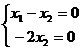 тогда
тогда 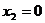 , и отсюда
, и отсюда 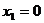 . После приведения к треугольному виду, последняя неизвестная получится 0, за ней и предпоследняя и т.д. Если матрица невырожденная, то решение единственно, но поскольку обязательно существует тривиальное, то единственное оно и есть тривиальное (все нули), других решений нет. Итак, сформулируем обнаруженный нами факт в виде теоремы:
. После приведения к треугольному виду, последняя неизвестная получится 0, за ней и предпоследняя и т.д. Если матрица невырожденная, то решение единственно, но поскольку обязательно существует тривиальное, то единственное оно и есть тривиальное (все нули), других решений нет. Итак, сформулируем обнаруженный нами факт в виде теоремы:
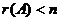 .
.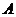 имеет нетривиальные решения
имеет нетривиальные решения 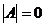 .
.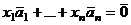 при некотором наборе ненулевых коэффициентов
при некотором наборе ненулевых коэффициентов 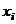
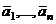 является линейно зависимой
является линейно зависимой 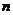
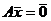 ,
, 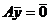 , тогда
, тогда 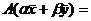
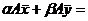
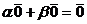 .
.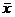 решение неоднородной системы,
решение неоднородной системы, 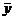 - решение соответствующей однородной системы (с той же основной матрицей, но 0 в правой части).
- решение соответствующей однородной системы (с той же основной матрицей, но 0 в правой части).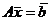 ,
, 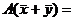
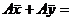
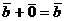 .
.
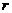 , то
, то  свободных переменных переносятся вправо, тогда можно построить по крайней мере не меньше, чем
свободных переменных переносятся вправо, тогда можно построить по крайней мере не меньше, чем 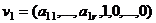
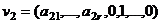
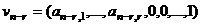
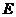 , т.е. заведомо ненулевой, равный 1.
, т.е. заведомо ненулевой, равный 1. 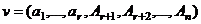 - решение однородной системы.
- решение однородной системы.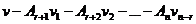 тоже является решением.
тоже является решением.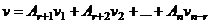 , то есть новое решение можно представить в виде такой линейной комбинации ранее найденных
, то есть новое решение можно представить в виде такой линейной комбинации ранее найденных 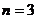 ,
, 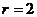 ). Решить однородную систему:
). Решить однородную систему: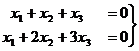
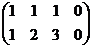


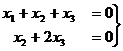 базисный минор можно заметить в первых двух столбцах, так что
базисный минор можно заметить в первых двух столбцах, так что 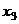 свободная переменная, переносим её вправо:
свободная переменная, переносим её вправо: 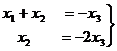 . Теперь последовательно выражаем через свободную переменную две базисные переменные.
. Теперь последовательно выражаем через свободную переменную две базисные переменные.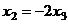 , а подставляя в 1-е, получим
, а подставляя в 1-е, получим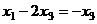 , т.е.
, т.е. 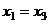 .
.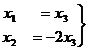 .
. 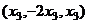 .
.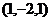 ,
, 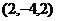 ,
, 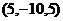 , и т.д.
, и т.д.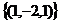 .
.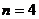 ,
, 
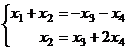 .
. 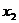 уже фактически выражено:
уже фактически выражено: 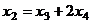 , подставим это в первое уравнение, чтобы выразить
, подставим это в первое уравнение, чтобы выразить 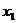 .
.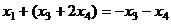
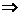
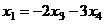 .
.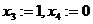
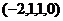
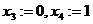
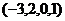 .
.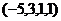 также является решением системы.
также является решением системы.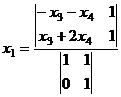 =
= 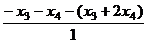
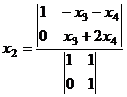 =
= 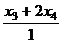
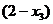 . А для однородной системы справа констант нет (они 0), но туда перенесены свободные переменные. Т.е. решение методом Гаусса во всех этих 3 параграфах выполняется похожим образом, только справа разные типы объектов.
. А для однородной системы справа констант нет (они 0), но туда перенесены свободные переменные. Т.е. решение методом Гаусса во всех этих 3 параграфах выполняется похожим образом, только справа разные типы объектов. над полем
над полем 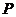 заданы 2 системы векторов:
заданы 2 системы векторов: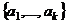 (1) и
(1) и 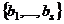 (2). Если каждый вектор системы (1) линейно выражается через систему (2), то будет говорить, что система (1) выражается через (2), обозначается
(2). Если каждый вектор системы (1) линейно выражается через систему (2), то будет говорить, что система (1) выражается через (2), обозначается 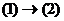 .
. 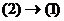 , то системы (1) и (2) называются эквивалентными,
, то системы (1) и (2) называются эквивалентными, 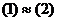 .
. 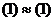 .
. 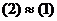 .
.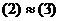 , то
, то 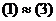 .
.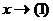 , то
, то 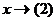 .
. . Но при этом
. Но при этом 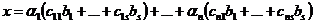 а в таком случае, можно перегруппировать слагаемые и получить
а в таком случае, можно перегруппировать слагаемые и получить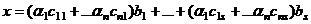 , то есть
, то есть 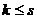 ;
; 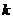 векторов, так, что оставшиеся векторы, вместе с векторами системы (1) составляют новую систему, эквивалентную (2).
векторов, так, что оставшиеся векторы, вместе с векторами системы (1) составляют новую систему, эквивалентную (2).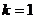 . Система (1) имеет вид
. Система (1) имеет вид 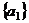 . Тогда во-первых очевидно, что
. Тогда во-первых очевидно, что  , так как (2) содержит хотя бы один вектор.
, так как (2) содержит хотя бы один вектор.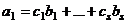 . Пусть в этом равенстве
. Пусть в этом равенстве 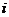 - наименьший индекс, для которого
- наименьший индекс, для которого 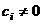 , т.е.
, т.е. 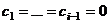 . Тогда можно вектор
. Тогда можно вектор 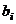 выразить через систему векторов
выразить через систему векторов 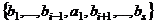 (3):
(3): 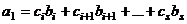
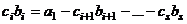
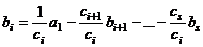 . Итак,
. Итак, 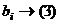 .
. 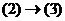 .
.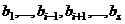 выражаются через (3), так как они принадлежат этой системе (достаточно взять один коэффициент 1, другие 0). А то, что
выражаются через (3), так как они принадлежат этой системе (достаточно взять один коэффициент 1, другие 0). А то, что  (2)
(2)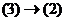 .
.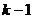 утверждение верно. Тогда существует система
утверждение верно. Тогда существует система (4),
(4),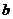 в системе (2).
в системе (2).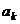 линейно выражается через (2), а значит, и через (4), так как
линейно выражается через (2), а значит, и через (4), так как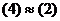 .
. 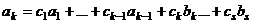 .
. 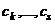 отличен от 0, иначе бы
отличен от 0, иначе бы , что противоречило бы линейной независимости системы (1).
, что противоречило бы линейной независимости системы (1).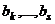 имеет ненулевой коэффициент (пусть для определённости это будет
имеет ненулевой коэффициент (пусть для определённости это будет 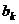 , иначе произведём перенумерацию) а значит, его можно выразить через систему
, иначе произведём перенумерацию) а значит, его можно выразить через систему 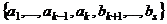 (5)
(5)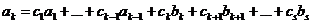
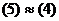 , но при этом было
, но при этом было 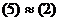 .
. 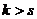 . Тогда на каком-то этапе замены, в системе (2) уже все векторы заменены на векторы из системы (1) (причём проведено
. Тогда на каком-то этапе замены, в системе (2) уже все векторы заменены на векторы из системы (1) (причём проведено 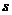 замен). Тогда при замене
замен). Тогда при замене 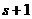 -го вектора мы столкнулись бы с тем, что
-го вектора мы столкнулись бы с тем, что 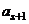 линейно выражается через систему
линейно выражается через систему 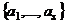 , то есть через подсистему системы (1). Но если какой-то вектор системы (1) линейно выражается через другие векторы этой же системы, это противоречит линейной независимости системы (1), которая по условию теоремы выполняется.
, то есть через подсистему системы (1). Но если какой-то вектор системы (1) линейно выражается через другие векторы этой же системы, это противоречит линейной независимости системы (1), которая по условию теоремы выполняется.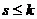 одновременно, а значит,
одновременно, а значит, 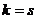 .
. 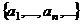 (1) бесконечная система элементов линейного пространства
(1) бесконечная система элементов линейного пространства 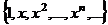 ЛНС. Любая конечная подсистема ЛНС.
ЛНС. Любая конечная подсистема ЛНС.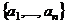 (1) один базис,
(1) один базис, 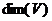 .
.  вектора, линейно зависима (очевидно, следует из определений выше).
вектора, линейно зависима (очевидно, следует из определений выше).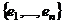 некоторый базис, значит, это максимальная линейно независимая система, поэтому при добавлении любого вектора
некоторый базис, значит, это максимальная линейно независимая система, поэтому при добавлении любого вектора 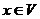 она становится линейно зависимой:
она становится линейно зависимой: 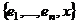 ЛЗС. Тогда при каком-то ненулевом наборе коэффициентов
ЛЗС. Тогда при каком-то ненулевом наборе коэффициентов  . При этом
. При этом 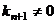 , иначе система
, иначе система 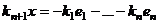 ,
, 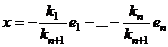 .
.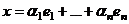 и
и 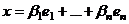 .
. 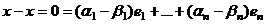 .
.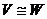 ,
, 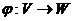 изоморфизм. Возьмём в
изоморфизм. Возьмём в 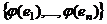 образует базис в
образует базис в 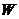 . По предыдущему следствию, она ЛНС. Тогда уже, как минимум,
. По предыдущему следствию, она ЛНС. Тогда уже, как минимум, 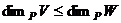 , так как в
, так как в 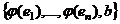 . Так как
. Так как 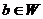 является образом некоторого элемента
является образом некоторого элемента 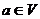 .
. ЛНС, но это невозможно, так как
ЛНС, но это невозможно, так как 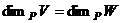 .
. 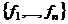 в
в  , то положим
, то положим  , то есть
, то есть 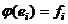 . Это действительно взаимно однозначное отображение. Если было бы не так, то например
. Это действительно взаимно однозначное отображение. Если было бы не так, то например 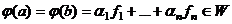 , тогда было бы
, тогда было бы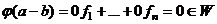 , т.е. ненулевому вектору поставили бы в соответствие (0,...,0), что противоречит построению
, т.е. ненулевому вектору поставили бы в соответствие (0,...,0), что противоречит построению 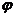 .
. =
=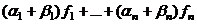 =
=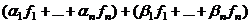 =
= 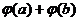 .
.  =
= 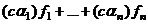 =
=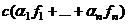 =
= 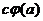 .
. 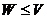 .
. 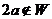 .
.

 2)
2) 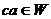
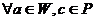 .
.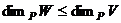 .
.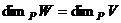 то
то  .
.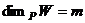 ,
,  . Допустим, что
. Допустим, что 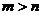 . Тогда существует линейно независимая система
. Тогда существует линейно независимая система  в пространстве
в пространстве 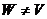 , то должен был бы существовать вектор
, то должен был бы существовать вектор 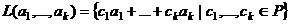 .
. 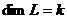 , если ЛЗС, то
, если ЛЗС, то  .
. , то в
, то в 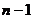 .
.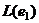 одномерно,
одномерно,  двумерно и т.д.
двумерно и т.д.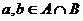 , то одновременно
, то одновременно 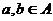 ,
, 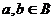 . Так как
. Так как 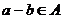 ,
, 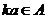 . При этом
. При этом 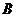 тоже подпространство, так что
тоже подпространство, так что 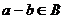 ,
, 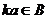 . Таким образом,
. Таким образом,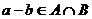 ,
, 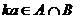 , а значит, по критерию подпространства,
, а значит, по критерию подпространства,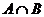 подпространство.
подпространство.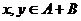 , то каждый из этих элементов представляется в виде:
, то каждый из этих элементов представляется в виде: 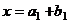 ,
, 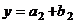 , где
, где 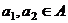 ,
, 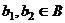 .
. 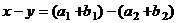 =
= 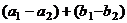 , каждое из
, каждое из 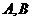 подпространство, значит,
подпространство, значит, 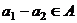 ,
, 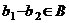 , то есть
, то есть 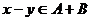 .
.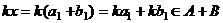 .
. 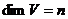 ,
, 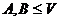 . Тогда:
. Тогда: 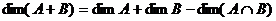 .
. 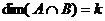 ,
, 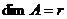 ,
, 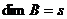 .
.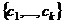 пространства
пространства 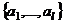 ,что система
,что система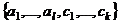 является базисом в
является базисом в 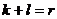 .
. 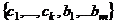 . Но так как размерность
. Но так как размерность 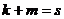 .
. 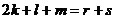
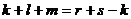 .
. 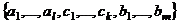 (3) возможно, базис в
(3) возможно, базис в 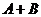 . (докажем).
. (докажем).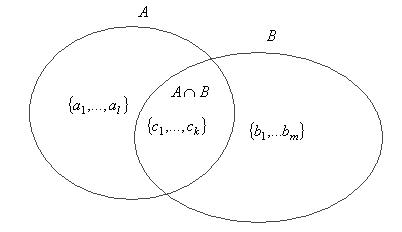
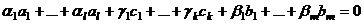 ,
, 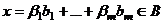 . Но тогда он равен
. Но тогда он равен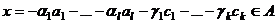 . Значит, этот вектор принадлежит пересечению
. Значит, этот вектор принадлежит пересечению 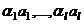 , т.е.
, т.е. 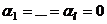 .
.


