
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Изоморфизм линейных пространств.
Определение. Пусть 1) 2) Если существует какой-либо изоморфизм Теорема 1. (об изоморфизме линейного пространства пространству векторов-строк). Пусть Тогда Доказательство. Пусть если Это отображение взаимно однозначно. Пусть
Тогда найдётся хотя бы одна Проверим сохранение операций.
Итак,
Теорема 2. Пусть
Доказательство. Обратно, пусть Поскольку
Следствие. Пусть
Теорема 3. (Об изоморфизме линейных пространств). Пусть
Доказательство. Необходимость. Пусть Тогда Достаточность. Пусть Построим изоморфизм так: если
Сохранение операций: 1)
2)
Лекция 12. 19.12.2020. Подпространства. Определение. Пусть Непустое подмножество его элементов, Тривиальные подпространства: 0 и Обозначение:
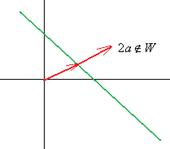
Вовсе не любое подмножество является подпространством. Например, если рассматривать все радиус-векторы, концы которых лежат на прямой, не проходящей через начало координат, то не получается подпространство. Сумма векторов (находится по правилу параллелограмма) оказывается не на этой прямой, впрочем, даже .
Теорема 1. (Критерий подпространства). Пусть Доказательство. Необходимость: если Достаточность. Пусть выполнено: 1) Из 1) следует, что Из 2) следует, что операция внешнего умножения порождает элемент снова из
Теорема 2. Пусть Если Доказательство. 1) Обозначим 2) Допустим,
Определение. Линейной оболочкой системы векторов По критерию подпространства, линейная оболочка является подпространством. Это подпространство, порождённое системой Если эти векторы образуют ЛНС, то Следствие. Если Действительно,
|
||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 198; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.67.26 (0.02 с.) |
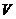 и
и 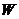 – линейные пространства над полем
– линейные пространства над полем 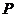 . Отображение
. Отображение 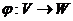 называется изоморфизмом, если оно взаимно однозначно и выполняются условия:
называется изоморфизмом, если оно взаимно однозначно и выполняются условия: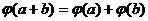
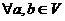 ,
,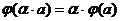
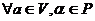 .
.  , где
, где 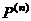 – пространство векторов-строк длины n над полем
– пространство векторов-строк длины n над полем 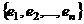 – какой-либо базис пространства
– какой-либо базис пространства 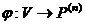 таким образом:
таким образом: , то
, то  .
.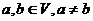 .
. ,
, 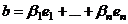 .
.  координата, что
координата, что 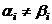 . Тогда они не совпадают и в
. Тогда они не совпадают и в 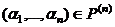 найдётся вектор
найдётся вектор 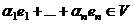 .
. 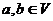 ,
,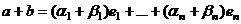 .
. 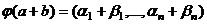 =
= 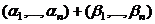 =
= 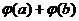 .
.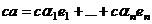
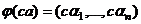 =
=  =
= 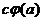 .
.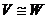 ,
, 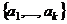 ЛЗС в
ЛЗС в 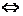
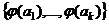 ЛЗС в
ЛЗС в 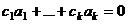 , тогда
, тогда 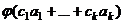 =
= 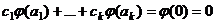 , то есть система
, то есть система 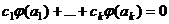 .
. , тоже являющееся изоморфизмом. Применим
, тоже являющееся изоморфизмом. Применим 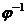 к сумме
к сумме 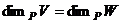 (они имеют одинаковую размерность).
(они имеют одинаковую размерность).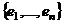 . Докажем, что система
. Докажем, что система 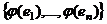 образует базис в
образует базис в 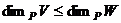 , так как в
, так как в  векторов,
векторов, 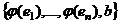 . Так как
. Так как 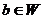 является образом некоторого элемента
является образом некоторого элемента 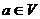 .
. ЛНС, но это невозможно, так как
ЛНС, но это невозможно, так как 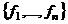 в
в  , то есть
, то есть 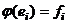 . Это действительно взаимно однозначное отображение. Если было бы не так, то например
. Это действительно взаимно однозначное отображение. Если было бы не так, то например 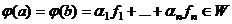 , тогда было бы
, тогда было бы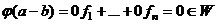 , т.е. ненулевому вектору поставили бы в соответствие (0,...,0), что противоречит построению
, т.е. ненулевому вектору поставили бы в соответствие (0,...,0), что противоречит построению 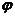 .
. =
=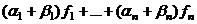 =
=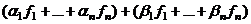 =
=  =
= 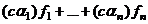 =
=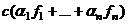 =
= 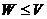 .
. 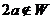 .
.

 2)
2) 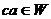
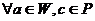 .
.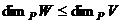 .
.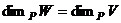 то
то  .
.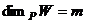 ,
,  . Допустим, что
. Допустим, что 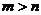 . Тогда существует линейно независимая система
. Тогда существует линейно независимая система  в пространстве
в пространстве 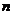 векторов, хотя его размерность равна
векторов, хотя его размерность равна 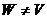 , то должен был бы существовать вектор
, то должен был бы существовать вектор 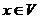 , который нельзя выразить через базис пространства
, который нельзя выразить через базис пространства 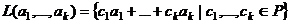 .
. 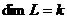 , если ЛЗС, то
, если ЛЗС, то  .
. , то в
, то в 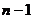 .
.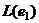 одномерно,
одномерно,  двумерно и т.д.
двумерно и т.д.


