
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Амплитудные и фазовые соотношения между током и напряжением для идеальных пассивных элементов линейной электрической цепиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим ситуацию, когда через сопротивление
Проводя сравнение поученного выражения с выражением (1.3), видим, что амплитуда и начальная фаза данного напряжения связаны с амплитудой и начальной фазой тока как:
Таким образом, амплитуды тока и напряжения связаны законом Ома, а их начальные фазы совпадают и, следовательно, ток и напряжение для сопротивления являются синфазными сигналами. Кроме этого видно, что ток и напряжение колеблются с одной и той же угловой частотой. Если тот же самый гармонический ток будет протекать через индуктивность
Тогда из сравнения выражений (1.18) и (1.3) вытекают следующие соотношения между амплитудами и начальными фазами тока и напряжения:
а мгновенные значения тока и напряжения, по-прежнему, изменяются с одной и той же угловой частотой. Структура первого из выражений (1.19) формально совпадает с законом Ома, однако вместо сопротивления
которую принято называть индуктивным сопротивлением. Величина, обратная индуктивному сопротивлению, называется индуктивной проводимостью и определяется как:
Таким образом, амплитуды тока и напряжения связаны законом Ома, а напряжение опережает ток по фазе на Пусть к внешним зажимам емкости приложено гармоническое напряжение вида (1.3), тогда согласно компонентному соотношению для данного элемента:
Из анализа полученного выражения и его сравнения с выражением (1.2) следуют следующие соотношения между амплитудами и начальными фазами тока и напряжения:
а мгновенные значения тока и напряжения, как и для предыдущих элементов, изменяются с одной и той же угловой частотой. Структура первого из выражений (1.23) формально совпадает с законом Ома, если заменить проводимость
которую принято называть емкостной проводимостью. Величина, обратная емкостной проводимости, называется емкостным сопротивлением и определяется как:
Таким образом, амплитуды тока и напряжения связаны законом Ома, а ток опережает напряжение по фазе на Поскольку токи и напряжения в рассмотренных идеальных пассивных элементах изменяются с одной и той же частотой, то любая реакция линейной электрической цепи, составленной из таких элементов, будет изменяться с этой частотой, причем величина частоты задается действующим в цепи источником тока или ЭДС. Такой режим работы линейной электрической цепи называется установившимся гармоническим режимом. Таким образом, чтобы записать закон изменения любой реакции линейной электрической цепи во времени согласно выражениям (1.2) или (1.3) достаточно определить ее амплитуду и начальную фазу. А значит, задача анализа линейной электрической цепи в установившемся гармоническом режиме сводится к отысканию амплитуд и начальных фаз всех реакций электрической цепи при заданных номиналах элементов, входящих в состав электрической цепи, способах их соединений (схеме электрической цепи) и задающем токе или ЭДС источника (источников), действующего в цепи.
|
|||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 681; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.42.25 (0.009 с.) |

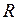 , входящее в состав некоторой линейной электрической цепи, протекает гармонический ток, мгновенное значение которого определяется выражением (1.2). Тогда согласно закону Ома для данного участка электрической цепи:
, входящее в состав некоторой линейной электрической цепи, протекает гармонический ток, мгновенное значение которого определяется выражением (1.2). Тогда согласно закону Ома для данного участка электрической цепи: . (1.16)
. (1.16)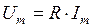 и
и 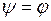 . (1.17)
. (1.17)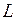 , то согласно компонентному соотношению для данного элемента:
, то согласно компонентному соотношению для данного элемента: . (1.18)
. (1.18) и
и 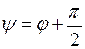 , (1.19)
, (1.19)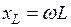 , (1.20)
, (1.20)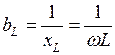 . (1.21)
. (1.21)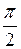 радиан, или на
радиан, или на 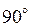 .
.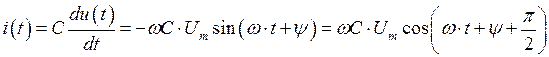 .(1.22)
.(1.22) и
и 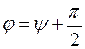 , (1.23)
, (1.23)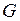 на комбинацию вида:
на комбинацию вида: , (1.24)
, (1.24)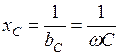 . (1.25)
. (1.25)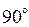 .
.


