
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Законы Кирхгофа и закон ома в комплексной форме. Комплексное и полное сопротивление и проводимостьСодержание книги
Поиск на нашем сайте
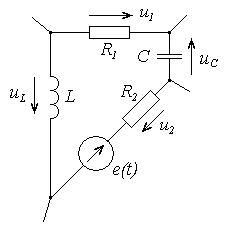
Рассмотрим произвольный контур электрической цепи (рис. 1.6).
Рис. 1.6 – Контур электрической цепи Согласно второму закону Кирхгофа выполняется равенство:
Воспользуемся соответствием (1.32) и перепишем данное равенство в виде:
или же
Поскольку данное равенство выполняется для любого момента времени
или же
то есть алгебраическая сумма комплексных амплитуд напряжений на элементах цепи, образующих контур, равна нулю. Это и составляет суть второго закона Кирхгофа в комплексной форме. Знак комплексной амплитуды, по-прежнему определяется совпадением или несовпадением направления напряжения с выбранным направлением обхода контура. Аналогичным образом рассмотрим произвольный узел электрической цепи (рис. 1.7).
Рис. 1.7 – Узел электрической цепи Согласно первому закону Кирхгофа выполняется равенство:
Воспользуемся соответствием (1.32) и перепишем данное равенство в виде:
или же
Поскольку данное равенство выполняется для любого момента времени
или же
то есть алгебраическая сумма комплексных амплитуд токов ветвей, сходящихся в любом узле электрической цепи, равна нулю. Это и составляет суть первого закона Кирхгофа в комплексной форме. Знак комплексной амплитуды, по-прежнему определяется направлением соответствующего тока ветви: знак «+» соответствует притекающим к узлу токам, а знак «-» - оттекающим от узла токам. Преобразуем аналогичным образом компонентные соотношения для сопротивления, индуктивности и емкости:
Воспользуемся соответствием (1.32) и перепишем данные равенства в виде:
Поскольку операции взятия вещественной части, умножения на константу, дифференцирования и интегрирования являются линейными, то они являются перестановочными и данные равенства можно переписать в виде:
Поскольку данное равенство выполняется для любого момента времени
или же
Данные выражения отражают суть закона Ома в комплексной форме: комплексная амплитуда напряжения на данном участке электрической цепи равна произведению комплексной амплитуды тока, протекающего по данному участку, и комплексного сопротивления данного участка. Таким образом, комплексные сопротивления резистивного, индуктивного и емкостного элементов равны:
При последовательном соединении элементов электрической цепи через них протекает один и тот же ток, а, значит, в выражения для закона Ома в комплексной форме будет входить одна и та же комплексная амплитуда тока. С другой стороны, напряжение на концах такого участка складывается из напряжений на отдельных элементах, а, значит, складываются и комплексные сопротивления этих элементов. Величина, обратная комплексному сопротивлению, носит название комплексной проводимости. Очевидно, что при параллельном соединении элементов электрической цепи напряжение на их зажимах одинаково, а, значит, в выражения для закона Ома в комплексной форме будет входить одна и та же комплексная амплитуда напряжения. С другой стороны, ток, притекающий к такому соединению, складывается из токов, протекающих по каждому из соединенных элементов, а, значит, складываются и комплексные проводимости этих элементов. Комплексные проводимости резистивного, индуктивного и емкостного элементов определяются выражениями:
Введенные комплексные сопротивление и проводимость имеют определенный физический смысл. Так модуль комплексного сопротивления некоторого участка электрической цепи, который носит название полного сопротивления этого участка, определяет соотношение между амплитудой напряжения на данном участке и тока, протекающего по нему. Аргумент комплексного сопротивления определяет сдвиг фаз между напряжением на данном участке и током, протекающим по нему. Рассмотрим примеры расчета линейных электрических цепей в рамках метода комплексных амплитуд.
ПРИМЕР 1
Определим в общем виде амплитуды и начальные фазы напряжений на сопротивлении и индуктивности для следующей электрической цепи:
Анализируемую цепь можно рассматривать в качестве двухполюсника, состоящего из последовательно соединенных сопротивления и индуктивности, к которому присоединен источник ЭДС.
Комплексное входное сопротивление этого двухполюсника равно:
По закону Ома находим комплексную амплитуду тока в цепи и напряжений на отдельных ее элементах:
где
ПРИМЕР 2
Определим в общем виде амплитуды и начальные фазы напряжений на сопротивлении и емкости для следующей электрической цепи:
Цепь представляет собой двухполюсник, состоящий из последовательно соединенных сопротивления и емкости, к которому присоединен источник ЭДС. Комплексное входное сопротивление этого двухполюсника равно:
По закону Ома находим комплексную амплитуду тока в цепи и напряжений на отдельных ее элементах:
где
ПРИМЕР 3
Определим в общем виде амплитуды и начальные фазы напряжений на сопротивлении, индуктивности и емкости для следующей электрической цепи:
Находим комплексное входное сопротивление:
где По закону Ома находим комплексную амплитуду тока в цепи и напряжений на отдельных ее элементах:
где
|
||||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 144; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.127.59 (0.009 с.) |

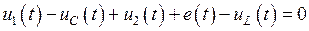 . (1.33)
. (1.33)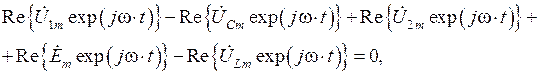
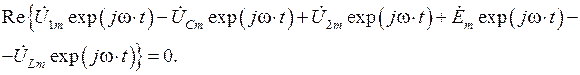
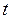 , то знак вещественной части можно опустить:
, то знак вещественной части можно опустить: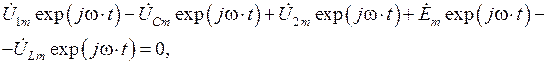
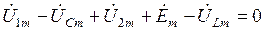 , (1.34)
, (1.34)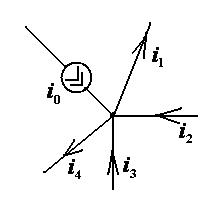
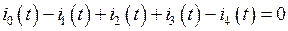 . (1.35)
. (1.35)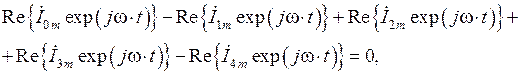
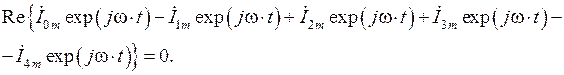
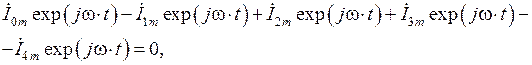
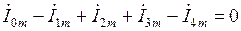 , (1.36)
, (1.36)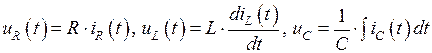 . (1.37)
. (1.37)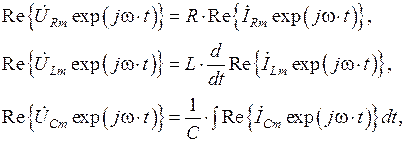
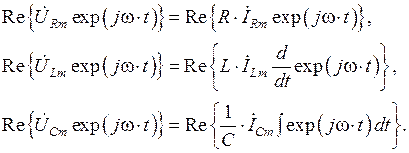
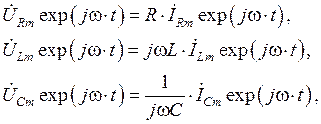
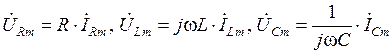 . (1.38)
. (1.38)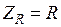 ,
, 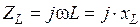 ,
, 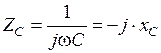 . (1.39)
. (1.39) ,
, 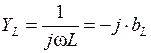 ,
, 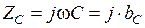 . (1.40)
. (1.40)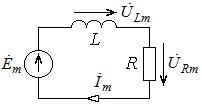
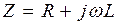 .
.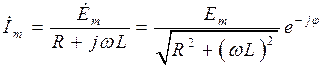 ,
,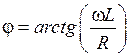 - аргумент комплексного входного сопротивления,
- аргумент комплексного входного сопротивления,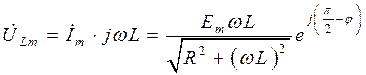 , (П1.1)
, (П1.1)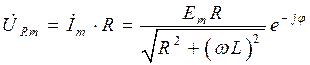 . (П1.2)
. (П1.2)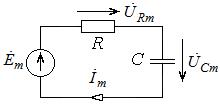
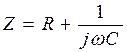 .
.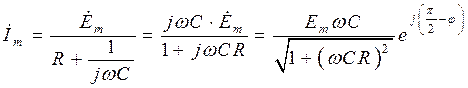 ,
,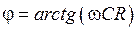 - аргумент комплексного входного сопротивления,
- аргумент комплексного входного сопротивления, , (П2.1)
, (П2.1)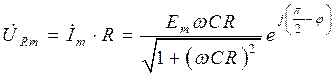 . (П2.2)
. (П2.2)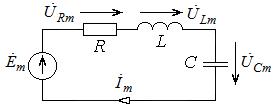
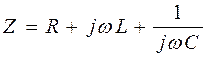 , или же
, или же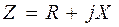 ,
,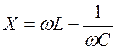 – реактивная составляющая комплексного входного сопротивления.
– реактивная составляющая комплексного входного сопротивления.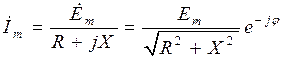 ,
,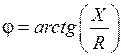 - аргумент комплексного входного сопротивления,
- аргумент комплексного входного сопротивления,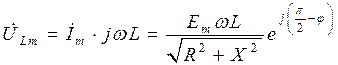 , (П3.1)
, (П3.1)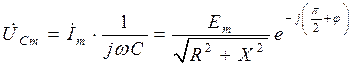 , (П3.2)
, (П3.2)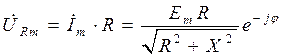 . (П3.3)
. (П3.3)


