
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 10. Расстояние от точки до прямой. Различные виды
уравнения плоскости
Расстояние от точки до прямой Ax + By + C = 0, из рисунка видим
До в общее уравнение прямой подставить координаты точки, взять по абсо- 38 Лютной величине и разделить на модуль нормального вектора. Пример 1. Треугольник задан своими вершинами А(1,2); В(-2,1); С(3,2). Найти длину его высоты, опущенной из вершины А. Решение. B h = АК. Высоту найдём, как расстояние от точки A K до прямой ВС. Уравнение ВС: h = Пример 2. Составить уравнения биссектрис углов между прямыми Решение.. M( приравняем, получим
В общем виде уравнения биссектрис углов между прямыми запишутся так:
Уравнение пучка прямых
Определение. Совокупность прямых, лежащих в плоскости и проходящих через одну точку называется пучком прямых с центром в этой точке. Пучок прямых можно задать уравнением с угловым коэффициентом: y-
Пример. Написать уравнение прямой, проходящей через точку М пересечения прямых 5x – y + 10 = 0 и 8x + 4y + 9 = 0 и параллельно прямой x + 3y = 0. Решение. Запишем уравнение пучка 5x – y+ 10 +
(5
РАЗЛИЧНЫЕ ВИДЫ УРАВНЕНИЯ ПЛОСКОСТИ В 39 Векторное уравнение плоскости z . 0 -ние плоскости. x z Уравнение плоскости, проходящей через данную точку.
Общее уравнение плоскости . M 0
точку или уравнение связки плоскостей. Раскроем скобки в последнем уравнении Аx+By+Cz – (A Выражение в скобках обозначим через D, получим:
Неполные уравнения плоскости
В общем уравнении полагаем: 1). D = 0 Ax + By + Cz = 0, плоскость проходит через начало координат. z
x 0 y
2). A = 0 By + Cz + D = 0, плоскость параллельна оси ox. z o y x
A =D =0 By + Cz =0, плоскость проходит через ось ox. z o y z x 3). В = 0 А x + Cz + D = 0, плоскость параллельна оси оy. o y 40 x B =D = 0 Ax + Cz = 0, плоскость проходит через ось оy. z o y x
4). C = 0 Ax + By + D = 0, плоскость параллельна оси oz.
z
x o y
C = D =0 Ax + By = 0, плоскость проходит через ось oz. z o y x 5). А = В =0 С z + D = 0, плоскость параллельна координатной плоскости XOY. z
o y x 6). A =C = 0 By + D = 0, плоскость параллельна координатной плоскости XOZ. z o y x
7). B = C = 0 Ax + D = 0, плоскость параллельна координатной плоскости YOZ. z o y x 8). A =B = D = 0 Cz = 0 или z = 0, координатная плоскость XOY. z o y x
9). B =C = D = 0 Ax = 0 или x = 0, координатная плоскость YOZ. z o z x y
10). А = С = D = 0 By = 0 или y = 0, координатная плоскость XOZ. o y x 41
Пример. Найти уравнение плоскости, проходящей через ось OX и точку М(1,2,3). Решение. Уравнение плоскости имеет вид By + Cz = 0; найдём В и С. Подставим координаты точки в это уравнение 2В + 3С = 0
Уравнение плоскости в отрезках
Рассмотрим общее уравнение плоскости Ax + By + Cz + D = 0. Перенесём D вправо и разделим на D:
отрезках, где a, b, c отрезки, которые плоскость отсекает от осей координат. Пример. Построить плоскость 2 x + 5 y – 10 = 0. Приведём это уравнение к уравнению в отрезках
o 2 y x 5
Лекция 11. Угол между плоскостями. Условия параллельности и перпендикулярности плоскостей.
1). Если
42 2). Если Пример 1. Составить уравнение плоскости, проходящей через точку Решение. 3(x+2y) + 2(y-1) – 7(z-4) = 0. Пример 2. Через точку Решение. Уравнение плоскости находим по формуле уравнения плоскости, проходящей через точку, то есть А(x + 2) + B(y – 3) + C (z – 6)=0. Из рисунка вид-
мой плоскости перпендикулярен нормальным векторам данных плоскостей.
Уравнение плоскости, проходящей через 3 различные точки,не лежащие на одной прямой
. М . . . ведения ( динатах
3 – и точки. Пример. Получить уравнение плоскости, проходящей через три известные точки: Решение. Найдём координаты векторов
43
получаем (x-1)5 – (y+1)(-5) + z 5 =0 или 5x+5y +5z =0. Ответ. x+y+z =0.
Уравнение плоскости в нормальном виде z . M0. M (
o x
(
Расстояние от точки до плоскости Задача. Найти расстояние от точки . d
Q
Решение. Воспользуемся формулой, которую применим без доказательства: Пример. Найти расстояние от точки Решение. d =
44 Прямая в пространстве
Линию в пространстве рассматривают, как множество всех точек, принадлежащих двум пересекающимся поверхностям Например: окружность. Прямую линию получим при пересечении двух плоскостей.
Общее уравнение прямой в Это уравнение, заданное пересечением двух плоскостей:
Пример. Построить прямую Решение. Чтобы построить прямую, надо задать две точки, для этого найдём точки пересечения прямой с координатными плоскостями. 1). Z =0, 2). X = 0, Определение. Точка пересечения прямой с координатной плоскостью называется следом прямой. Z . М2
o. М1 y x
Векторное уравнение прямой. Параметрические уравнения прямой. Канонические уравнения
Пусть прямая L задана точкой M1
o y x 45 прямой.
Вектор Пример. Привести уравнение прямой к каноническому виду Решение
Уравнение прямой, проходящей через две точки
М2 y x прямой,проходящей через 2-е точки Пример1. Найти уравнение прямой, проходящей через точку Решение. Уравнение прямой будем искать в каноническом виде:
46 дение нормальных векторов плоскостей, задающих прямую, то есть
| Поделиться:
| |
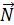

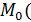 x0,y0) Пусть прямая задана общим уравнением
x0,y0) Пусть прямая задана общим уравнением
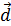 =
= 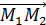 = (
= (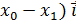 +(
+(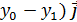

 ∙
∙ 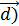 =
= 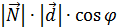 ;
; 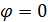 или π
или π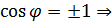 (
( =
=  . В координатах
. В координатах 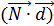 = А(
= А(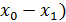 +B(
+B( = A
= A 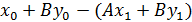 , так как точка
, так как точка  , то её координаты удовлетворяют уравнению прямой поэтому А
, то её координаты удовлетворяют уравнению прямой поэтому А 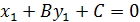 или A
или A 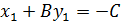 , подставим. (
, подставим. (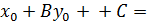
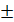
 отсюда находим
отсюда находим 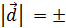
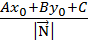 или
или Вывод. Чтобы найти расстояние от точки до прямой, на-
Вывод. Чтобы найти расстояние от точки до прямой, на-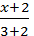 =
= 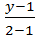
 или x -5y+ 7 = 0.
или x -5y+ 7 = 0.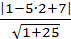 =
= 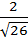 . Ответ. h =
. Ответ. h = 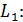 3x-4y-2=0 и
3x-4y-2=0 и 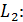 5x +12y – 1= 0.
5x +12y – 1= 0.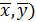

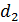
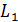
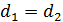 ,
, 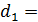
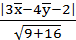 ,
, 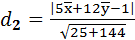 ,
, 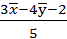 =
= 
 ; 14x-112y-21=0 и
; 14x-112y-21=0 и  64x + 8y – 21=0.
64x + 8y – 21=0.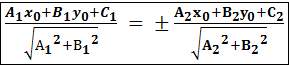
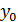 =k(x-
=k(x- 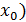 , а можно с помощью двух прямых:
, а можно с помощью двух прямых: 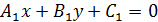 и
и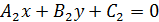 .
.  уравнение пучка прямых.
уравнение пучка прямых.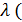 8x + 4y + 9) = 0.
8x + 4y + 9) = 0.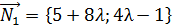 ,
, 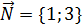 . Векторы
. Векторы 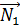
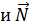 параллельны, в координатах
параллельны, в координатах  отсюда 15 + 24
отсюда 15 + 24 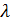 - 4
- 4 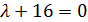
 =
=  =
= 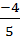
 x – (
x – (
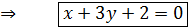 .
.
 ⊥
⊥  → (
→ (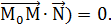 Из рисунка
Из рисунка 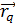 M видно
M видно 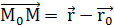 , поэтому
, поэтому 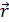 y
y 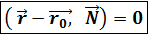
 векторное урав-
векторное урав- 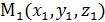 ; M((x, y, z);
; M((x, y, z); 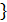
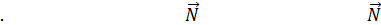 { A,B,C}
{ A,B,C} 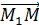 ⊥
⊥ 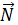 →
→  В координатах:
В координатах:  → уравнение плоскости через
→ уравнение плоскости через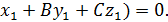
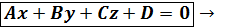 общее уравнение плоскости.
общее уравнение плоскости.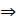 В =
В = 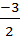 С подставляем в уравнение
С подставляем в уравнение 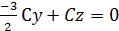 , сокращаем на С, окончательно
, сокращаем на С, окончательно 
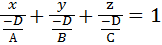 , обозначим
, обозначим 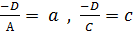
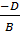 = b, уравнение примет вид:
= b, уравнение примет вид: 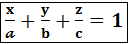
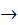 уравнение плоскости в
уравнение плоскости в  На оси ox отложим отрезок x = 5, на оси oy отложим отрезок y = 2. z
На оси ox отложим отрезок x = 5, на оси oy отложим отрезок y = 2. z Плоскости заданы общими уравнениями.
Плоскости заданы общими уравнениями. 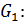
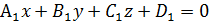 и
и


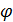

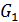
 =
= 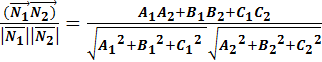
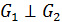 , то (
, то (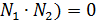 или в координатах
или в координатах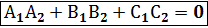 →условие перпендикулярности плоскостей.
→условие перпендикулярности плоскостей. , то
, то  в координатах
в координатах  →условие параллельности плоскостей.
→условие параллельности плоскостей.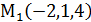 параллельно плоскости 3x + 2y – 7z +8 = 0.
параллельно плоскости 3x + 2y – 7z +8 = 0.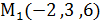 провести плоскость, перпендикулярную плоскостям
провести плоскость, перпендикулярную плоскостям 
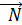 ⊥
⊥  , поэтому
, поэтому 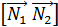 =
= 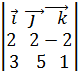 = 13
= 13 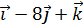 .
. { 13, -8, 1 }. Ответ.
{ 13, -8, 1 }. Ответ. 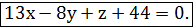
 ;
;  ;
; М(x,y,z). Соединим эти точки векторами, усло-
М(x,y,z). Соединим эти точки векторами, усло- 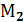 вие принадлежности 3-х векторов одной плоскос-
вие принадлежности 3-х векторов одной плоскос- ти- равенство нулю их смешанного произ-
ти- равенство нулю их смешанного произ-  или в коор-
или в коор- 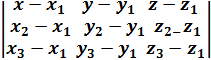 = 0 →уравнение плоскости, проходящей через
= 0 →уравнение плоскости, проходящей через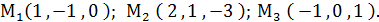
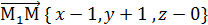 ;
; 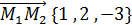 ;
; 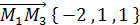 . Уравнение плоскости запишем в виде:
. Уравнение плоскости запишем в виде: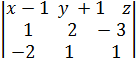 = 0, раскрываем определитель по элементам 1-й строки,
= 0, раскрываем определитель по элементам 1-й строки,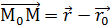 ,
, 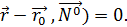
 ,
, 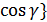 .
.
 +
+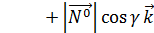 ,
, 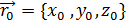 ,
, 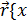 ,y, z}
,y, z} 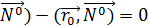 , но (
, но (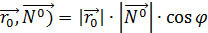
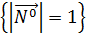 =
= 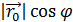 =прN
=прN 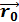 = p
= p  , подставим в скалярное произведение и перейдём к координатам
, подставим в скалярное произведение и перейдём к координатам  →нормальное уравнение плоскости, где величина р равна ортогональной проекции радиуса вектора фиксированной точки плоскости на единичный вектор нормали.
→нормальное уравнение плоскости, где величина р равна ортогональной проекции радиуса вектора фиксированной точки плоскости на единичный вектор нормали. до плоскости Q: Ax+By+Cz+D=0.
до плоскости Q: Ax+By+Cz+D=0. (x1 ,y1,z1)
(x1 ,y1,z1) 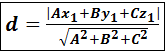 →формула расстояния от точки до плоскости.
→формула расстояния от точки до плоскости.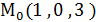 до плоскости 3x+4y+5z+3=0.
до плоскости 3x+4y+5z+3=0. =
= 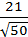 . Ответ. d =
. Ответ. d = 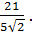

 и
и 
 при пересечении сферы и плоскости получаем
при пересечении сферы и плоскости получаем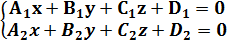 → общее уравнение прямой.
→ общее уравнение прямой.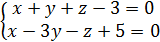
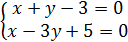 решаем эту систему, находим точку пересечения
решаем эту систему, находим точку пересечения  .
.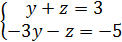
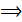
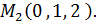
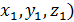 и направляющим вектором
и направляющим вектором  .
.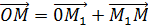 ;
;  , поэтому
, поэтому
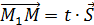 , где t – скалярный параметр
, где t – скалярный параметр 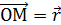 ,
,  , из рисунка видим
, из рисунка видим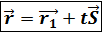 → векторное уравнение
→ векторное уравнение 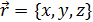 ;
; 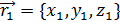 ; t
; t 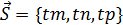 , в координатах векторное уравнение запишется так:
, в координатах векторное уравнение запишется так: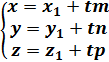 → параметрические уравнения прямой.
→ параметрические уравнения прямой.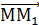 = { x -
= { x - 
 в координатах
в координатах 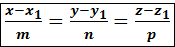 → канонические уравнения прямой
→ канонические уравнения прямой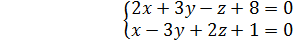
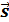
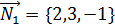 ;
; 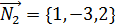 ,
, 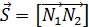 =
=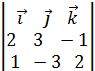 = 3
= 3  . Чтобы найти точку на прямой, в общем уравнении положим z=0,
. Чтобы найти точку на прямой, в общем уравнении положим z=0,  , решив эту систему, получим
, решив эту систему, получим  и запишем каноническое уравнение
и запишем каноническое уравнение 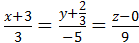 . Ответ.
. Ответ. 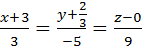 .
. 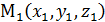 ;
; 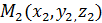
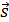
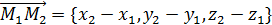 ;
;  ;
; 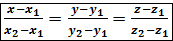 → уравнение
→ уравнение , параллельно прямой
, параллельно прямой 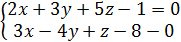 .
.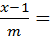
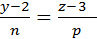 . Направляющий вектор
. Направляющий вектор 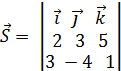 = 23
= 23  + 13
+ 13 


