Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Правило. Чтобы найти производную от неявной функции , нужно дифференцировать по X обе части уравнения с учётом , что y зависит от X по правилам дифференцирования сложной функции.
Пример. Найти y’, если функция y задана уравнением: xy2 = Решение. ( xy2)’=(
Дифференцирование сложно - показательной функции
Определение. Сложно – показательной функцией называется функция, у которой и основание и показатель степени являются функциями от x, например: (sin x
Теорема. Если y = Доказательство. Прологарифмируем функцию y, Y’ = y [ v’ Пример1. Найти y’, если y = (sin x Логарифмируем обе части равенства
84 Ответ. Y’ = (sin x Пример 2. Найти y’, если y = Решение. Сначала найдём логарифм данной функции
Ответ. Y’ = Приём для нахождения производной с применением логарифмирования называется логарифмическим дифференцированием, а выражение Производные высших порядков
Так как f’(x) есть функция, то её можно снова дифференцировать. Определение. Производная от 1-ой производной функции называется производной 2-го порядка. Определение. Производной n-го порядка функции y = f(x) называется первая производная от производной (n-1) – го порядка. Обозначается: y(n), f(n), F(n)(x) = [ f(n-1)(x)]’. Пример. Найти производную Решение. Сначала найдём y’. Y’ = Ответ.
Производная второго порядка от неявных функций
Рассмотрим на примере. Пример. Найти производную второго порядка от функции y, заданной неявно
x = Решение. Дифференцируем обе части равенства, предполагая, что y сложно зависит от x. 1 = =
85 Другой способ. Первый раз дифференцируем уравнение, задающее функцию, получаем 1 =
Механический смысл производной второго порядка Пусть s = f(t) – путь, пройденный материальной точкой за время t, v = v(t) – скорость за это время, точке t +
Определение. Ускорением за время t называется предел среднего ускорения при Вывод. Ускорение прямолинейного движения точки равно второй производной пути по времени.
Производные функций, заданных параметрически
Пусть
Чтобы найти вторую производную, воспользуемся формулой для первой производной, обозначим Можно находить вторую производную по другой формуле Пример. Найти вторую производную от функции y, заданную параметрически x = si Решение. Найдём сначала y’x. y’x = =
86
|
|||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 226; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.233.41 (0.013 с.) |
 .
.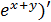 .
.  y2 + 2xyy’ =
y2 + 2xyy’ = 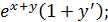 y2 + 2xyy’ =
y2 + 2xyy’ = 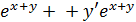 ; сгруппируем члены, содержащие y’, получим y’(2xy -
; сгруппируем члены, содержащие y’, получим y’(2xy - 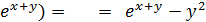 , отсюда y ’ =
, отсюда y ’ = 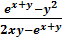
 ;
; 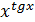 ;
; 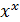 ; (
; (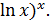 Обозначается y = [u(x)
Обозначается y = [u(x)  =
= 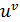 .
.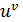 , то
, то  .
. затем дифференцируем последнее равенство по правилу дифференцирования неявной функции (
затем дифференцируем последнее равенство по правилу дифференцирования неявной функции (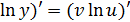 →
→ 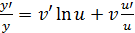 из этого равенства выразим y’.
из этого равенства выразим y’.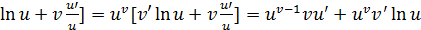 ч.т.д.
ч.т.д.
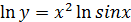 , дифференцируем
, дифференцируем 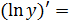
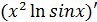

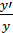 = 2x
= 2x 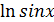 +
+ 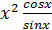
 ]
]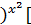 2x
2x 
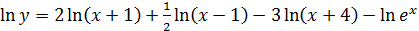 , дифференцируем обе части, получим
, дифференцируем обе части, получим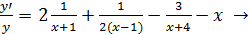 y’ = y[
y’ = y[ 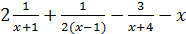 ]
]  [
[ 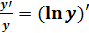 - логарифмической производной.
- логарифмической производной. - четвёртого порядка для функции y =
- четвёртого порядка для функции y = 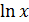 .
. , y’’ = (
, y’’ = ( =-
=- 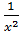 ; y’’’ = (-
; y’’’ = (-  =
= 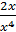 =
= 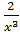 ; y’’’’ =(
; y’’’’ =( .
.
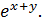
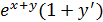 , выражаем отсюда y’, y’=
, выражаем отсюда y’, y’= 
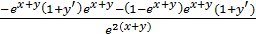 =
= 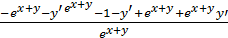 =
= 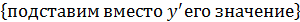 =
=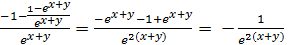 .
.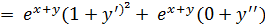 , отсюда выражаем y’’. Y’’ = - (1+y’
, отсюда выражаем y’’. Y’’ = - (1+y’  , подставляем значение для y’, y’’ = - (1 +
, подставляем значение для y’, y’’ = - (1 + 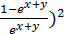 = - (
= - (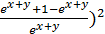 = -
= - 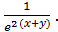
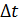 соответствует скорость v1(t+
соответствует скорость v1(t+ 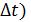 ,
, 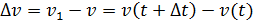 , ускорение
, ускорение 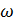
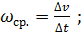
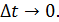
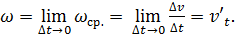

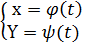 , а
, а 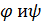 имеют производные, причём t =
имеют производные, причём t = 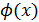 , тогда y=
, тогда y= 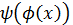
 t
t 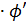 x, на основании теоремы о дифференцировании обратной функции запишем
x, на основании теоремы о дифференцировании обратной функции запишем 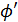 x =
x = 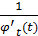 подставим в y’x =
подставим в y’x = 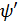 t
t 
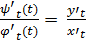 .
. 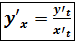 .
.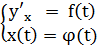 ,
, 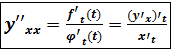 .
.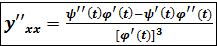
 ; y = sin 2t
; y = sin 2t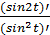 =
= 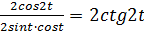 ; y’’xx =
; y’’xx =  =
=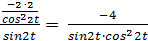 . Ответ. y’’xx =
. Ответ. y’’xx =