
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 24. Дифференциал функции. ⇐ ПредыдущаяСтр 10 из 10
Пусть функция y = f (x) дифференцируема на некотором интервале, тогда Y’ =
Определение. Дифференциалом функции называется главная часть приращения функции, линейная относительно Обозначается Вывод. Дифференциал независимой переменной равен приращению этой переменной Пример. Найти дифференциал функции y = Решение. f’(x) =
Приближённые вычисления с помощью дифференциала функции Запишем приращение функции y = f(x) F (x0 + Пример. Вычислить sin 460. Решение. Пусть f(x) = sin x; f’(x) = cos x; sin(x+ Примем x0 + Sin460 = sin ( Ответ. Sin460 Свойства дифференциала функции Задача нахождения дифференциала функции сводится к нахождению производной функции, так как 1). d(u 2). d(u
87 3). d( Пример 1. Найти дифференциал функции y = Решение. dy =
Пример 2. Найти дифференциал функции y, если sin(x+y) =
Решение. Функция y задана неявно, найдём сначала y’. Дифференцируем обе части равенства cos(x+y)(1+y’) = Y’ =
Инвариантность формы дифференциала функции Если y = f(u) , где u = du Вывод. Форма дифференциала не зависит от того, является аргумент функции независимой переменной или функцией другого аргумента. Пример. Найти дифференциал функции y = sin Решение. y = sinu, u =
Геометрическое значение дифференциала функции
y M1 T M N 0 x x+
М(x,y); M 1(x+ NT = f’(x) Вывод. Дифференциал функции f(x), соответствующий значениям x и
Замечание. В данном случае
88 y N
M2 Т М1 0 x NT = dy
Дифференциалы высших порядков
Пусть задана функция y = f(x), дифференциал которой dy = f’(x) dx является в свою очередь также функцией от x. Определение. Дифференциал от дифференциала функции называется дифференциалом второго порядка этой функции и обозначается d2y. d(dy) = d2y; d2y = [f’(x)dx]’dx, так как dx = Пример. Найти дифференциал второго порядка для функции y= Решение. dy = (
89 С О Д Е Р Ж А Н И Е Предисловие - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 3 Линейная алгебра Лекция 1. Определители, их свойства, вычисление - - - - - - - - - - - - - - - 4 Лекция 2. Понятие матрицы. Основные операции над матрицами. Собственные числа и собственные векторы матрицы - - - - - - - - - - - - - - - - - - - 8 Лекция 3. Матричная запись и матричное решение системы уравнений 1-го порядка. Ранг матрицы - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 12 Лекция 4. Общая теория решения систем уравнений - - - - - - - - - - - - - 16 Элементы векторной алгебры Лекция 5. Понятие вектора. Основные операции над векторами - - - - - - -20 Лекция 6. Длина вектора. Направляющие косинусы - - - - - - - - - - - - - - 25 Лекция 7. Скалярное произведение векторов. Векторное произведение - - - 27 Лекция 8. Выражение векторного произведения векторов через координаты перемножаемых векторов. Смешанное произведение - - - - - - - - - - - - - 29
Аналитическая геометрия Лекция 9. Основные понятия.Различные виды уравнения прямой на плоскости - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 33 Лекция10. Расстояние от точки до прямой. Различные виды уравнения плоскости - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 38 Лекция11. Угол между плоскостями. Условия параллельности и перпендикулярности плоскостей - - - - - - - - - - - - - - - - - - - - - - - 42 Лекция12. Взаимное расположение прямой и плоскости в R3. Полярная система координат - - - - - - - - - - - - - - - - - - - - - - - - - - 47 Лекция 13. Кривые второго порядка - - - - - - - - - - - - - - - - 51 Лекция 14. Поверхности второго порядка - - - - - - - - - - - - - - 53 Лекция 15. Преобразование прямоугольной системы координат в R2. Квадратичные формы - - - - - - - - - - - - - - - - - - - - - - - - - - 57
Математический анализ Лекция 16. Понятие множества, функции, предела функции - - - - - - 61 Лекция 17. Основные теоремы о бесконечно малых функциях и о пределах при x Лекция18. Второй классический предел. Сравнение бесконечно малых функций - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 68 Лекция19. Непрерывность функции. Последовательности - - - - - - - - 71 91 Лекция20. Комплексные числа. Действия над комплексными числами - - 74 Лекция 21. Определение производной, её механический, геометрический смысл. Основные правила дифференцирования - - - - - - - - - - - - -77
Лекция22. Производные некоторых элементарных функций - - - - - - - 81 Лекция 23. Неявные функции и их дифференцирование. Производные высших порядков - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 84 Лекция 24. Дифференциал функции - - - - - - - - - - - - - - - - - - 87 Литература - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 90 Содержание- - - - - - - - - - - - - - - - - - - - - - - - - - - - - 91
92 Л И Т Е Р А Т У Р А 1. Власов В.Г. Конспект лекций по высшей математике. М.: Айрис. 1996.287с. 2. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч. 1. М.: Высш. шк., 2003.-415с. 3. Письменный Д.Т. Конспект лекций по высшей математике. Ч.1,2.- 2-е изд.,- М.: Айрис – пресс, 2003.- 546 с. 4. Труппова В.А. и др. Теория функций комплексного переменного. Конспект лекций и практических занятий. – Иркутск:Из-во ИрГТУ, 2007-60с. 5. Шнейдер В.Б. и др. Краткий курс высшей математики. М.: Высш. шк. Ч.1., 1972.- 285с.
90
|
|||||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 91; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.233.54 (0.108 с.) |
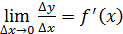 по теореме (
по теореме ( о пределе функции, имеем
о пределе функции, имеем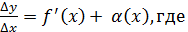
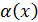 → б.м.функция, при
→ б.м.функция, при  ,
,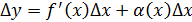 , f’(x)
, f’(x) 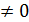 поэтому f’(x)
поэтому f’(x) 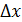 - б.м. 1-го порядка малости относительно
- б.м. 1-го порядка малости относительно  Найдём
Найдём  =
= 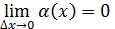 , то есть
, то есть  более высокого порядка малости, чем
более высокого порядка малости, чем 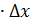 называется главной частью приращения функции.
называется главной частью приращения функции.
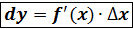 . Если y= f(x) = x, то y’x = 1, а
. Если y= f(x) = x, то y’x = 1, а 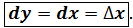
 ,
, 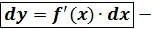 рабочая формула.
рабочая формула.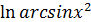 .
.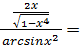
 , dy =
, dy = 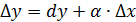 , так как последнее слагаемое более высокого порядка, то его отбросим и получим
, так как последнее слагаемое более высокого порядка, то его отбросим и получим 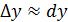 или
или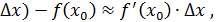 отсюда
отсюда 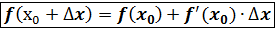 - формула для приближённого вычисления с помощью дифференциала функции.
- формула для приближённого вычисления с помощью дифференциала функции.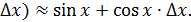
 , тогда
, тогда  0 =
0 = 
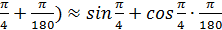 =
= 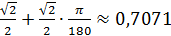 .
. .
. 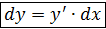 , поэтому все свойства производной распространяются и на дифференциал:
, поэтому все свойства производной распространяются и на дифференциал:
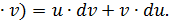
 .
.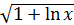 .
.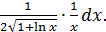
 .
.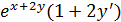 отсюда выражаем y’.
отсюда выражаем y’.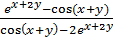 =
=  , dy =
, dy = 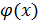 , y = f[
, y = f[  , то
, то  = f’u (u)
= f’u (u) 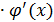 → dy = f’u
→ dy = f’u 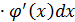
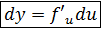 .
.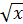 .
. .
.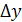
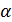
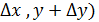 ; NT = MN
; NT = MN 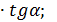 tg
tg 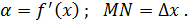
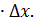 →
→ 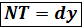
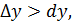 но возможно и
но возможно и 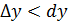 .
. 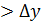
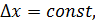 то d2y = [ f’(x)
то d2y = [ f’(x)  ]’
]’ 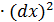 , принято записывать (dx)2 = dx2, аналогично d3y = f’’’(x)
, принято записывать (dx)2 = dx2, аналогично d3y = f’’’(x) 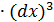 ……
…… 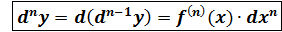
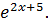
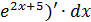 =2
=2 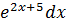 ; d2y = (2
; d2y = (2 
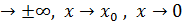 - - - - - - - - - - - - - - - - - - - - - - - 65
- - - - - - - - - - - - - - - - - - - - - - - 65


