
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 21. Определение производной , её механический , геометрический смысл. Основные правила дифференцирования.Содержание книги
Поиск на нашем сайте
Пусть имеем непрерывную функцию y = f(x). 77 1). Дадим приращение x 2). Составим 3). Определение. Производной функции y=f(x) в точке x называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремиться к 0. (При условии, что этот предел существует). Записывается так: f ’ (x) = Определение. Правой (левой) производной функции f(x) в точке x0 называется предел справа (слева) отношения приращения функции к приращению аргумента при стремлении последнего к нулю. f’(x0 Операция нахождения производной функции f(x) называется дифференцированием этой функции.
Механический смысл производной S0 =f(t0), S = f(t0+ Vcp.=
ти, так как в начале отрезка точка может двигаться очень быстро, а потом может и наоборот медленно.Поэтому, чтобы точнее охарактеризовать движение пользуются пределом, то есть тот предел к которому стремиться средняя скорость при V = Вывод. Скорость неравномерного движения в данный момент есть предел отношения приращения пути
m = f(x), В физике средняя плотность стержня на отрезке от x0 до x0+ Определение. Плотностью 78 плотности, когда длина отрезка Вывод. Плотность – это производная массы по длине x.
Геометрический смысл производной
Пусть f(x) – непрерывная функция. y секущая y0 x0 x0+
kкас. = tg k кас . = tg Вывод. Производная функции в точке x 0 есть угловой коэффициент касательной, проведённой в точку x 0 к кривой. Воспользуемся уравнением прямой с угловым коэффициентом: y-y0 = tg Определение. Нормалью к кривой y=f(x) в данной точке
Определение. Угол между двумя кривыми, заданными уравнениями y = f1 ( x) и y = f2 (x) в их общей точке М0 ( x0,y0) понимается угол
79
y f1
f2 0 x
Дифференцируемость функции
Определение. Если функция y= f(x) в точке x = x0,имеет производную, то есть существует Теорема. Если функция y= f(x) – дифференцируема в точке x0, то она в этой точке непрерывна. Доказательство. Так как функция дифференцируема, то Замечание. Обратное утверждение неверно. Y
x0 0 x Из рисунка видно, что в точке x0 функция непрерывна, а касательная, проведённая к графику функции в этой точке параллельна оси ox, то есть tg
Основные правила дифференцирования
1. [ c 2. [u(x) 3. [u(x) 4.
80 Теорема о сложной функции
П Теорема. Если u = Доказательство. Дадим x приращение
|
||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 131; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.73.85 (0.008 с.) |

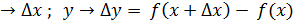 .
.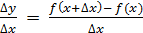 .
.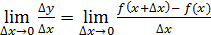
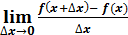 = y ’ =
= y ’ = 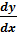 .
.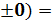
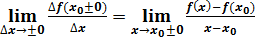 .
. . Пусть материальная точка движется по прямой по закону s=f(t), где t – время, а s- путь за время t.
. Пусть материальная точка движется по прямой по закону s=f(t), где t – время, а s- путь за время t.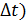 ,
, 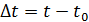
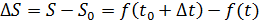
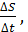 средняя скорость не отра-
средняя скорость не отра-  t0
t0  s жает истинного изменения скорос-
s жает истинного изменения скорос-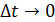 .
.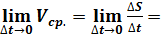 S’(t).
S’(t).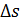 к приращению времени
к приращению времени  . Пусть дан тонкий прямолинейный неоднородный стержень длины
. Пусть дан тонкий прямолинейный неоднородный стержень длины 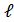 .
.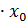
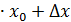
 Масса стержня есть функция точки
Масса стержня есть функция точки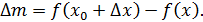
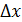 находится по формуле
находится по формуле 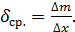
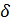 стержня в точке x0 называется предел средней
стержня в точке x0 называется предел средней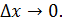
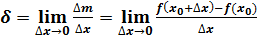 = mx ’
= mx ’ 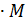 касательная
касательная 
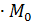
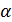 0
0 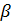
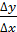 , при
, при 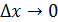 секущая будет стремиться занять положение касательной, то есть
секущая будет стремиться занять положение касательной, то есть 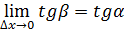 . Таким образом
. Таким образом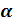 =
= 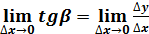 .
.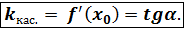 – геометрический смысл производной.
– геометрический смысл производной.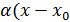 ) или
) или 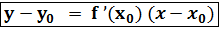 - уравнение касательной к графику функции y=f(x).
- уравнение касательной к графику функции y=f(x).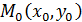 называется прямая перпендикулярная к касательной, проведённой к графику функции y=f(x) в точке М0.
называется прямая перпендикулярная к касательной, проведённой к графику функции y=f(x) в точке М0.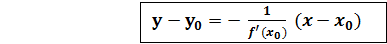 - уравнение нормали
- уравнение нормали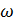 между касательными М0 А и М0 В к этим кривым в точке М0.
между касательными М0 А и М0 В к этим кривым в точке М0.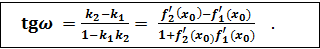
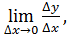
 то функция называется дифференцируемой при x = x0.
то функция называется дифференцируемой при x = x0.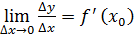 , а по теореме (
, а по теореме ( это значит
это значит 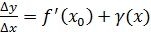 , где
, где 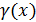 б.м.функция, отсюда
б.м.функция, отсюда 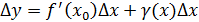 ,
, 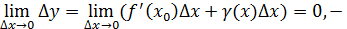 это условие непрерывности функции ч.т.д..
это условие непрерывности функции ч.т.д..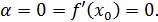
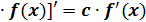 , c = const.
, c = const.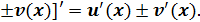
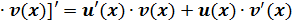 .
.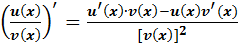 .
.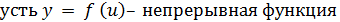 и u =
и u = 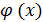 - непрерывна, тогда функция y = f [
- непрерывна, тогда функция y = f [ 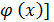 - сложная функция.
- сложная функция.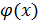 имеет производную u’(x) в точке x,а y = f(u) → y’(u) в точке u, то y =f[
имеет производную u’(x) в точке x,а y = f(u) → y’(u) в точке u, то y =f[ 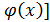 в данной точке x имеет производную y’x, которая находится по формуле:
в данной точке x имеет производную y’x, которая находится по формуле: 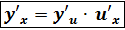
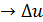 . Составим очевидное тождество
. Составим очевидное тождество 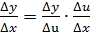 , перейдём к пределу
, перейдём к пределу 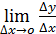 =
= 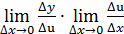 =
= 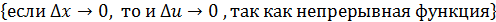 , поэтому
, поэтому 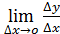 =
= 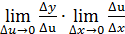 = y’u
= y’u 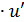 x ч.т.д..
x ч.т.д..


