
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
ЛЕКЦИЯ 8. Выражение векторного произведения через координаты перемножаемых векторов . Смешанное произведение.
Пусть вектор [ 29
ВЫВОД. Векторное произведение равно определителю третьего порядка, элементами которого являются базисные векторы Замечание. Векторное произведение базисных векторов 0
Пример 1. Сила Решение.
Ответ: Пример 2. Вычислить площадь параллелограмма, построенного на векторах Решение. S = Пример 3. Вычислить площадь треугольника, вершины которого находятся в точках А (2,3,1); В (5, 6, 3); С (7, 1, 10). Решение. S = этого из координат конца вычтем координаты начала, получим
Cмешанное произведение векторов Определение. Смешанным произведением 3-х векторов Обозначается: (
Cвойства смешанного произведения
1). ([ 2). ( 3). (α Доказательство этих свойств следует из свойств определителей, что мы и увидим в дальнейшем. Геометрический смысл смешанного произведения (
Вывод: Смешанное произведение векторов с точностью до знака равно объёму параллелепипеда, построенного на векторах сомножителях. Координатная форма смешанного произведения
Пусть вектор [ 31 (
Используя формулу ( Пример. Вычислить объём пирамиды с вершинами в точках : О (0,0,0); А(5,2,0); В (2, 5, 0); С (1,2,4). Решение. Объём пирамиды равен Ответ: Vпир. = 84 куб. ед.
Условие компланарности векторов
Теорема. Необходимым и достаточным условием компланарности 3-х векторов является равенство нулю их смешанного произведения. Доказательство необходимости. Пусть Доказательство достаточности. Пусть (
Вывод: Условием компланарности векторов является равенство нулю их смешанного произведения Пример. Проверить лежат ли четыре точки в одной плоскости. А (2,-1,1); В(5,5,4); С(3,2,-1); Д(4,1,3). Решение. Надо проверить лежат ли 3 вектора ( не лежат в одной плоскости. Определение. Двойным векторным произведением векторов 32 Задачи
Задача 1. Какому условию должны удовлетворять векторы Задача 2. Точка 0 является центром тяжести треугольника АВС. Доказать, что
Задача 3. Найти сумму и разность векторов Задача 4. Дан вектор Задача 5. Даны 3 вектора
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Лекция 9. Основные понятия. Различные виды уравнения прямой на плоскости. Аналитическая геометрия имеет своей задачей изучение свойств геометрических объектов при помощи аналитического метода. В основе этого метода лежит метод координат, впервые применённый Декартом (великий французский математик и философ 1596-1650). Начальные (основные) понятия аналитической геометрии – точка, прямая линия, плоскость, поверхность.
Понятие об уравнении линии.
Определение. Линия L – это геометрическое множество точек, координаты которых удовлетворяют уравнению
Ф(x,y) = 0 или (1) F(x,y) = 0. Для более удобного построения линий L, часто вводят вспомогательную переменную или параметр t. Исключив из (2) параметр t, перейдём к (1). Пример. Получить уравнение окружности с центром в начале координат и радиусом r. Решение. Сделаем рисунок. 33
y
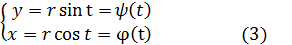
oo t x 0
Эти уравнения (3) и есть параметрические уравнения окружности. Обе части уравнений (3) возведём в квадрат и сложим Можно вывести уравнение циклоиды – это линия, которую описывает точка М на окружности, если окружность без скольжения движется по прямой. y
0 x
Определение. Линия называется алгебраической, если в некоторой декартовой системе координат она определяется уравнением Ф(x,y)=0, где Ф(x,y) – алгебраический полином – многочлен. Определение. Алгебраическая линия называется порядка n, если Ф(x,y) многочлен n-ой степени. Ф(x,y)= Аx+By+C=0 1-ой степени Ф(x,y)= A Ф(x,y)= A Определение. Всякая неалгебраическая линия называется трансцендентной.
УРАВНЕНИЕ ПОВЕРХНОСТИ И ЛИНИИ В ПРОСТРАНСТВЕ
Определение. Уравнение Ф(x,y,z)=0 называется уравнением поверхности S относительно д.с.к., если этому уравнению удовлетворяют координаты x,y,z, любой точки, лежащей на поверхности S.
0 x y М(x,y,z); С(a,b,c) МС =r=
34 Определение. Линию в
РАЗЛИЧНЫЕ ВИДЫ УРАВНЕНИЯ ПРЯМОЙ НА ПЛОСКОСТИ
Общее уравнение прямой. y N M M1 0 x ( A(x- Ax + By +(-A (-Аx-By)=C,получим
Неполные уравнения прямой.
1). С=0, Ax+ By=0 - прямая проходит через начало координат. 2). B=0, Ax+ C =0 - прямая параллельна оси оy. 3). A=0, By+ C =0 - прямая параллельна оси ox. 4). B=C=0, Ax=0, x=0 - ось oy. 5). А=С=0, Вy =0, y=0 - ось оx. Уравнение прямой в отрезках.
Запишем общее уравнение прямой Ax+By+C=0 0 x
Пример. Привести уравнение прямой 3x+5y+20= 0 к уравнению в отрезках. Решение. Перенесём 20 вправо и разделим обе части на -20, получим:
Ответ.
35 Каноническое уравнение прямой. Параметрические уравнения.
Определение. Вектор коллинеарный прямой, называется направляющим вектором прямой y M x уравнение прямой.
Если Обозначим
Уравнение прямой, проходящей через две точки y 0 Уравнение прямой с угловым коэффициентом. y 0 x
36 уравнении скобки y = kx + (- b, это постоянное число, получим:
Угол между двумя прямыми. Условия параллельности, перпен- дикулярности двух прямых
Если
Если
Условие параллельности
Y Y = 0
37 tg Если Если Пример. Получить все виды уравнения прямой, если прямая задана общим уравнением 3x+4y-5=0. Решение. 1). Уравнение с угловым коэффициентом: 4y=-3x+5 2).Уравнение прямой в отрезках: 3x+ 4y =5 3).Каноническое уравнение: возьмём 2 произвольные точки на прямой 4). Уравнение прямой через две точки
| Поделиться:
| |
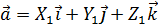 и вектор
и вектор 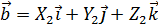 найдём векторное произведение этих векторов
найдём векторное произведение этих векторов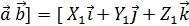 ,
, 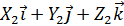 ] =
] = 
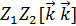 = {
= {  =
= 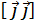 =
= 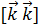 =0, } =
=0, } = 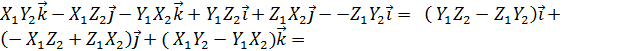 =
= 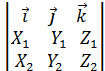 = { раскроем этот определитель по элементам первой строки, получим
= { раскроем этот определитель по элементам первой строки, получим 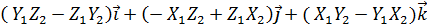 } = [
} = [ 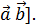
 (первая строка), координаты перемножаемых векторов
(первая строка), координаты перемножаемых векторов  (вторая строка);
(вторая строка); 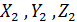 (третья строка ).
(третья строка ). 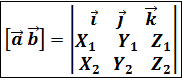
 находят по правилу правых и левых троек
находят по правилу правых и левых троек =
= 
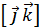 =
= 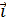
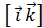 =-
=- 
 =
=  = -
= - 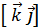 = -
= - 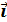
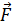 = {1, 0, 4 } приложена к точке С (1, 2, 3). Найти момент этой силы относительно точки D (1, 4, 5).
= {1, 0, 4 } приложена к точке С (1, 2, 3). Найти момент этой силы относительно точки D (1, 4, 5). ,координаты вектора
,координаты вектора  = { 0, -2, -2}.
= { 0, -2, -2}.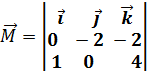 = -8
= -8 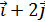 + 2
+ 2 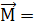 { -8,2,2}.
{ -8,2,2}.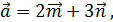

 , где
, где  ; угол между векторами
; угол между векторами 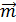 и
и  равен 600.
равен 600.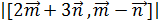 =
= 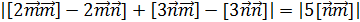 = 5
= 5 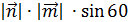 0 = 5
0 = 5  3
3 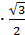 =15
=15 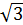 кв.ед. Ответ: S = 15
кв.ед. Ответ: S = 15 
 S =
S =  . Найдём координаты векторов
. Найдём координаты векторов 
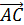 , для
, для {3,3,2}; 30
{3,3,2}; 30 {5,-2,9}. S =
{5,-2,9}. S =  =
= 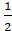
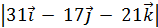 = =
= = 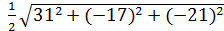 =
= 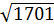 ед. Ответ: S =
ед. Ответ: S = 
 ,
, 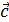 называется скалярное произведение вектора [
называется скалярное произведение вектора [ 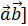 на вектор
на вектор  , ([
, ([ 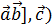 .
.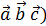 или (
или (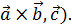
 ;
; = (
= (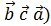 = - (
= - (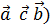 = +(
= +( ;
; ,
, 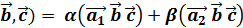 .
.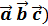
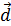
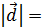 S. По определению ([
S. По определению ([ 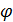 h =
h = 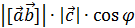 = S
= S  =
= 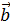 ={h =
={h = 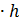 = V.
= V. 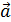 Угол
Угол  и >
и >  < 0 или
< 0 или  >0, поэтому
>0, поэтому 
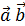 ] =
] = 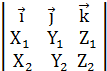 =
= 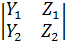 -
-  +
+ 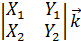 . Известно, что скалярное произведение - это произведение одноимённых координат, поэтому
. Известно, что скалярное произведение - это произведение одноимённых координат, поэтому X3 -
X3 - 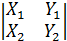 Z3 , c другой стороны - это разложение определителя третьего порядка по элементам третьей строки.
Z3 , c другой стороны - это разложение определителя третьего порядка по элементам третьей строки. = (
= ( 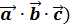 (
( 
 , можно доказать все свойства (1,2,3) смешанного произведения.
, можно доказать все свойства (1,2,3) смешанного произведения. объёма параллелепипеда, то есть = Vпир. =
объёма параллелепипеда, то есть = Vпир. =  Vпар. =
Vпар. = 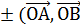 ,
, 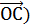 =
=  =
= 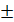 ( 100 -16) = 84 куб.ед.
( 100 -16) = 84 куб.ед. компланарны, значит построить параллелепипед на них нельзя, то есть объём равен нулю V=0, а это значит и
компланарны, значит построить параллелепипед на них нельзя, то есть объём равен нулю V=0, а это значит и  =0 ч.т.д.
=0 ч.т.д. 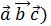 = 0 это значит, что V=0 и векторы
= 0 это значит, что V=0 и векторы 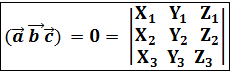 = 0
= 0 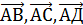 в одной плоскости, для этого найдём координаты этих векторов
в одной плоскости, для этого найдём координаты этих векторов 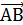 {3,6,3};
{3,6,3}; 
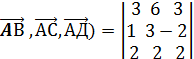 = 18 -24 +6 -18-12+ 12= 18
= 18 -24 +6 -18-12+ 12= 18 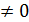 . Вывод. Эти точки
. Вывод. Эти точки  называется векторное произведение [
называется векторное произведение [ 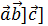 или [
или [  .
.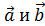 , чтобы вектор
, чтобы вектор  делил пополам угол между векторами
делил пополам угол между векторами 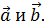
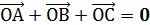 .
. , если
, если 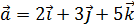 ;
; 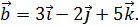
 ;
;  Угол
Угол  равен 600. Найти
равен 600. Найти  =?
=?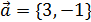 ,
, 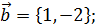
 Определить разложение вектора
Определить разложение вектора  по базису
по базису 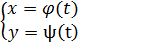 (2)
(2)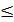 t
t 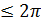
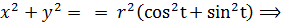
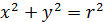 .
. 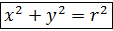
 уравнение окружности с центром в точке О(0,0) и радиусом r.
уравнение окружности с центром в точке О(0,0) и радиусом r.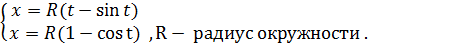
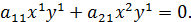
 2-ой степени
2-ой степени 3-й степени.
3-й степени.
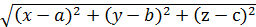 или
или - это уравнение сферической поверхности
- это уравнение сферической поверхности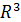 рассматривают, как пересечение 2-х поверхностей.
рассматривают, как пересечение 2-х поверхностей.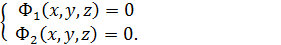

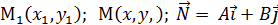 .
. =
= 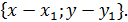
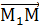

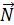 .
.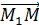 ∙
∙  , раскроем скобки
, раскроем скобки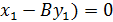 , обозначим
, обозначим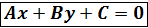 - общее уравнение прямой.
- общее уравнение прямой.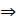 Ax+By=-C, разделим обе части на -С, получим
Ax+By=-C, разделим обе части на -С, получим  +
+  =1, обозначим
=1, обозначим  =
= 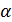 ,
,  = b.
= b. 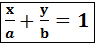
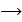 уравнение прямой в отрезках, α и b → отрезки, отсекаемые прямой от осей координат соответственно оx, оy. y
уравнение прямой в отрезках, α и b → отрезки, отсекаемые прямой от осей координат соответственно оx, оy. y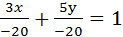 или
или 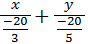 =1, α=
=1, α=  , b=
, b= 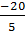 .
.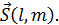
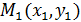 ; M(x,y);
; M(x,y); 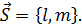
 ;
; 
 L
L  поэтому
поэтому 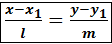
 то
то 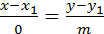 прямая параллельна оси оy. Если m=0, то
прямая параллельна оси оy. Если m=0, то 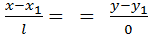 прямая параллельна оси оx.
прямая параллельна оси оx.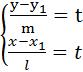
 параметрические уравнения прямой.
параметрические уравнения прямой.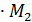
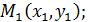
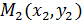 ;
; 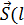 ,m); пусть
,m); пусть 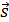
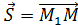 , тогда
, тогда 
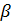
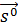 =
=  +
+  .
. ,
, 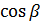 }.
}.  =
=  , подставим вместо
, подставим вместо  и m
и m 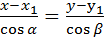 , но
, но 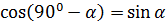 . Получим
. Получим 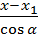 =
= 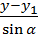
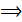
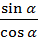 (x-
(x-  = y-
= y- 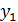 или tg
или tg 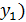 , окончательно
, окончательно 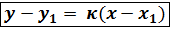
 Выражение в скобках обозначим через
Выражение в скобках обозначим через 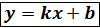 это уравнение прямой с угловым коэффициентом, где b отрезок, который прямая отсекает от осей координат.
это уравнение прямой с угловым коэффициентом, где b отрезок, который прямая отсекает от осей координат. . Пусть две прямые
. Пусть две прямые 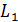 и
и 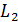 заданы общими уравнениями.
заданы общими уравнениями.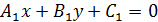 и
и 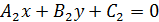 ;
; 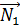 {
{ 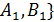 ;
;  {
{ 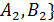
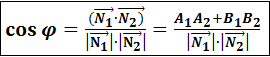
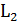
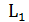 ║
║ 
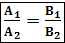 → условие параллельности.
→ условие параллельности. , это значит
, это значит  → условие перпендикулярности.
→ условие перпендикулярности.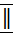 . Пусть две прямые
. Пусть две прямые 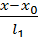 =
=  и
и  =
= 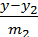 ,
, 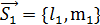 ,
, 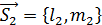 , то
, то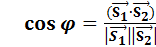 =
= 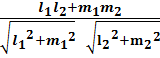
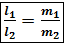 . Условие перпендикулярности
. Условие перпендикулярности 
 . Прямые
. Прямые 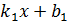 и y =
и y = 
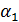
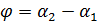 , tg
, tg 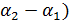 =
= x =
x =  , так как tg
, так как tg  ,
, 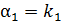 , то
, то 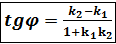 .
.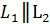 , то tg
, то tg 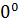 =0 и tg
=0 и tg 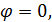 когда
когда 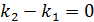 или
или 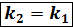 - условие параллельности прямых.
- условие параллельности прямых.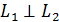 , то tg
, то tg  , поэтому 1+
, поэтому 1+ 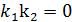 или
или 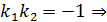
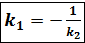 - → условие перпендикулярности прямых.
- → условие перпендикулярности прямых. 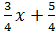 , k=-
, k=-  .
.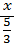 +
+ 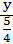 = 1,
= 1, 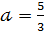 , b=
, b=  .
. (0,
(0, 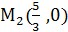 вектор
вектор 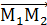 {
{  ,
, 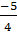 } является направляющим вектором прямой, каноническое уравнение запишем через точку
} является направляющим вектором прямой, каноническое уравнение запишем через точку 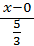 =
= 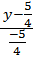 .
.


