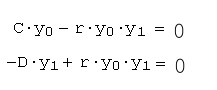Решение систем оду в одной заданной точке

     Достаточно часто при решении дифференциальных уравнений требуется определить значения искомых функций не на всём интервале (t0,t1), а только в последней его точке. Весьма распространены задачи поиска аттракторов динамических систем. Известно, что одна и та же система при разных  начальных условиях  при tà∞ приходит  в одну и ту же точку (аттрактор). Поэтому нужно определить эту точку.

   Для решения этой задачи в Mathcad   имеются модификации встроенных функций Rkadapt и  Bulstoer. Они имеют  другой набор параметров и работают быстрее своих аналогов.

· Rkadapt(y0,t0,t1,acc,D,k,s)-метод Рунге-Кутта с переменным шагом;

· Bulstoer(y0,t0,t1,acc,D,k,s)-метод Булирша-Штера:

o y0-вектор начальных значений в точке t0;

o t0,t1-начальная и конечная точки расчёта;

o acc-погрешность вычисления;

o D-векторная функция, задающая систему ОДУ;

o K-максимальное число шагов, на которых численный метод будет находить решение;

o S-минимально допустимая величина шага.

Пример:

Поиск аттрактора системы двух ОДУ модели осциллятора.

В первых двух строках определяется система уравнений и начальные условия; в следующей строке матрице u присваивается решение, полученное с помощью bulstoer.

В четвёртой строке определяем количество шагов, далее осуществлен вывод решения системы.

 

 

 

Жёсткие системы ОДУ

  Жесткие системы - это те уравнения, решение которых получить намного проще с помощью определенных неявных методов, чем с помощью явных методов.

Раccмотрим пример нежёсткого уравнения, решение которого получаем методом Рунге-Кутта.

 

 

 

 

Изменим коэффициент на -50:

 

 

 

 

    Разброс решения говорит о неустойчивости алгоритма. Первое, что можно сделать, - увеличить количество шагов в методе Рунге-Кутта.

Можно убедиться, что при step>20 разболтка пропадает, и решение становится похожим на график с коэффициентом -10.

 

 

 

 

 

 

       

 

 

     Таким образом, во-первых, мы выяснили, что одни и те же уравнения (с разными параметрами) могут быть как жесткими, так и нежесткими.

   Во-вторых, чем жестче уравнение, тем больше шагов в обычных численных методах требуется для его устойчивого решения.

      Решение жёстких систем дифференциальных уравнений можно осуществить только с помощью встроенных функций:

· Radau(y0,t0,t1,M,F)-алгоритм RADAUS для жёстких систем;

· Stiffb(y0,t0,t1,M,F,J) –алгоритм Булирша-Штера для жёстких систем ОДУ;

· Stiffr(y0,t0,t1,M,F,J) –алгоритм Розенброка для жёстких систем ОДУ;

o Y0-вектор начальных значений в точке t0;

o t0,t1-начальная и конечная точка расчёта;

o M-число шагов численного метода;

o F-векторная функция F(t,y) размера  1xN, задающая систему ОДУ.

o J-матричная функция  J(t,y) размера (N+1)xN, составленная из вектора  производных функции F(t,y) по t.

 

 

Пример:

Рассмотрим предыдущую функцию, только с коэффициентом -100.

 

 

  Существуют встроенные функции, которые применяются  для решения жёстких систем ОДУ не на всём интервале, а только в заданной точке t1.

· Radau(y0,t0,t1,acc,F,k,s)-алгоритм RADAUS;

· Stiffb(y0,t0,t1,acc,F,J,k,s) –алгоритм Булирша-Штера;

· Stiffr(y0,t0,t1,acc,F,J,k,s) –алгоритм Розенброка;

Примеры динамических моделей

    Динамическими системами принято называть класс задач, представленных задачами Коши для дифференциальных уравнений (обыкновенных - иначе ОДУ, или в частных производных) или систем таких уравнений.

     Наиболее просты примеры исключительно линейных уравнений, т. е. содержащих только первую степень неизвестных функций и их производных, как, к примеру модель линейного гармонического осциллятора. Линейные дифференциальные уравнения легко решаются аналитически, а необходимость применения численных методов возникает, когда число таких уравнений в системе ОДУ очень велико. Линейные ОДУ хорошо изучены, и в них могут существовать лишь простые типы аттракторов (центр, фокус, седло).

  Тип аттрактора характеризуется  свойствами конкретных динамических систем.   Различают следующие типы аттракторов - особых точек в фазовом пространстве

 

                  Узел:                                                          Центр:

               Фокус:                                                   Седло:

 

   Аттракторы могут быть либо устойчивыми (тогда траектории в фазовом пространстве стремятся к ним), так и неустойчивыми (тогда траектории, даже начинающиеся очень близко от особой точки, отталкиваются от нее - такие особые точки называют репеллерами).

   Помимо особых точек существуют аттракторы - предельные циклы, а также очень необычные странные аттракторы:

Предельный цикл:                                         Странный аттрактор:

 

    Между тем, многие нелинейные уравнения демонстрируют совершенно удивительные свойства, причем решение подавляющего большинства из них можно получить лишь численно. Рассмотрим несколько наиболее известных классических примеров систем ОДУ.

     Это модели нелинейного осциллятора, динамики популяций (Вольтерра), электронного генератора автоколебаний (Ван дер Поля), турбулентной конвекции жидкости (Лоренца) и химической реакции с диффузией (Пригожина).

  Все примеры являются типичными динамическими системами и содержат производные по времени t, описывая динамику различных физических параметров. Приведем  примеры и графики решений и фазовые портреты для некоторых  моделей.

Модель "хищник-жертва"

      Модель взаимодействия "хищник-жертва" независимо предложили в 1925-1927 гг. Лотка и Вольтерра. Два дифференциальных уравнения моделируют временную динамику численности двух биологических популяций жертвы y₀ и хищника y₁. Предполагается, что жертвы размножаются с постоянной скоростью C, а их численность убывает вследствие поедания хищниками. Хищники же размножаются со скоростью, пропорциональной количеству пищи (с коэффициентом r) и умирают естественным образом (смертность определяется константой D).

      Модель замечательна тем, что в такой системе наблюдаются циклическое увеличение и уменьшение численности и хищника  и жертвы, так часто наблюдаемое в природе. Фазовый портрет системы представляет собой концентрические замкнутые кривые, окружающие одну стационарную точку, называемую центром. Как видно, модельные колебания численности обеих популяций существенно зависят от начальных условий - после каждого периода колебаний система возвращается в ту же точку. Динамические системы с таким поведением называют негрубыми.