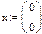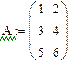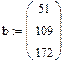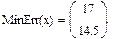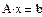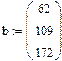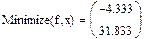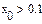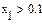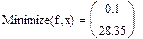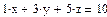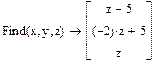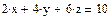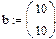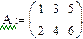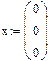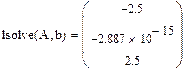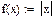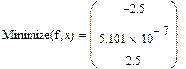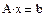Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение слау с использованием вычислительного блока Given / FindСодержание книги
Поиск на нашем сайте
Дана система линейных уравнений. Найти её решение. 3x 7x x 6x Алгоритм выполнения: 1. Ввести начальные значения корней 2. Ввести ключевое слово Given 3. Через логическое равно ввести все уравнения системы\ 4. Записать Find(x) 5. Установить знак =
Если система содержит большое количество уравнений, удобнее применять матричную форму. Алгоритм выполнения: 1.Ввести матрицу коэффициентов при неизвестных 2. Ввести вектор свободных членов 3. Ввести начальные значения корней через вектор 4. Ввести ключевое слово Given 5. Записать систему в матричной форму 6. Применить метод Find 7. В вычислительном блоке логическое равно.
Самый простой способ решения почти всякой несингулярной системы является алгоритм исключения Гаусса. Алгоритм исключения Гаусса Алгоритм последовательных исключений Гаусса основан на преобразовании матрицы A линейной системы Ax = b к треугольному виду (т.е. к форме, когда все элементы ниже главной диагонали матрицы являются нулевыми). Точнее, СЛАУ Ax = b заменяется эквивалентной системой с другой матрицей A* и другим вектором правых частей b*, но имеющей то же решение, что и исходная система. Алгоритм состоит в следующем: 1. Проводится прямой ход исключения неизвестных путем подстановки одних уравнений в другие. Используются следующие формулы: 2. При помощи обратного хода определяются все неизвестные х. Для этого хN сразу определяется из последнего уравнения, в которое не входят другие х (матрица системы теперь является трехдиагональной). Затем хN подставляется в предыдущее уравнение, из которого сразу определяется хN-1 и т.д. Этот метод реализован во встроенной функции lsolve. При использовании этого метода система уравнений должна быть записана в матричной форме. Алгоритм выполнения: 1. Ввести матрицу с коэффициентами при неизвестных 2. Ввести столбец свободных членов 3. Записать функция lsolve 4. При численном решении после функции ставится знак =, а
Произвольные системы линейных уравнений
Классические задачи решения систем линейных уравнений предполагают равное количество уравнений и неизвестных. Рассмотрим теперь системы, в которых матрица коэффициентов при неизвестных является неквадратной либо плохо обусловлена.
Переопределённые системы Рассмотрим систему уравнений, в которой число уравнений больше, чем число неизвестных, т.е. матрица А – прямоугольная. Чаще всего такие системы не имеют решений, т.е. являются несовместными или переопределёнными. Несовместные системы не могут быть решены с помощью вычислительного блока Given/Find. Пример:
1. Через оператор присваивания вводим матрицу коэффициентов и вектор свободных членов. 2. Решаем данную систему методом Гаусса 3. Вводим приблизительные решения корней в вектор х 4. Включаем вычислительный блок 5. Записываем а*х=в 6. Находим корни Find(x)= 7. Mathcad выдаст ошибку.
В редких случаях система с прямоугольной матрицей может оказаться совместной (если выбран соответствующий вектор b).
На практике задачи отыскания решения переопределённых систем линейных уравнений встречаются довольно часто. Точного решения такой системы не найти. Рассмотрим математическую постановку задач решения систем с прямоугольной матрицей. Вместо точного решения следует организовать поиск такого вектора х, который будет наилучшим образом удовлетворять всем уравнениям, т.е. минимизировать их невязку (расхождение между вектором А*х и вектором свободных членов b). Так как невязка A*x-b является векторной величиной, то минимизации надо подвергать её норму (т.е. скаляр) |A*x-b|. Т.е. принято искать не точное решение (которого просто нет), а псевдорешение-вектор, минимизирующий норму невязки системы уравнений. Задача решения линейной системы уравнения заменяется задачей отыскания глобального минимума функции f(x)=|A*x-b|. Поскольку эта минимизируемая норма зависит от суммы квадратов компонент неизвестного вектора, то процедура поиска псевдорешения является реализацией метода наименьших квадратов. Для решения задач минимизации невязки системы уравнений в Mathcad предусмотрены две встроенные функции Minerr и Minimize. Если используется функция Minerr, то используется ключевое слово Given, а в первом случае явно определяется функция f(x), подлежащая минимизации.
2-й способ:
Во-первых, сравнивая результаты, можно обнаружить, что они абсолютно различны, причём более похож на правильный ответ, выдаваемый функцией Minimize. Разгадка заключается в особенностях применения численного алгоритма, заложенного в функцию MinErr. Алгоритм заложен линейный, тип алгоритма можно изменить по правой кнопке мыши. Установить на нелинейный, выбрать метод из трёх предложенных. Во-вторых, приближённое решение c использованием Given невозможно при наличии дополнительных условий, выражающих вспомогательную априорную информацию о постановке задачи. В результате исходная задача сводится к условной минимизации функции f(x) c использованием дополнительных неравенств.
Пример: Поиск псевдорешения при наличии априорной информации
При выборе нелинейного алгоритма появляются отрицательные ответы, а при добавлении дополнительных условий в задачу решения ещё раз меняются.
Недоопределённые системы Рассмотрим системы с количеством уравнений меньшим количества неизвестных. Такие системы имеют либо бесконечное множество решений, либо не имеют решения вовсе. Решим аналитически систему двух уравнений с тремя неизвестными при помощи символьного процессора.
Но для решения недоопределённых систем, состоящих из большего числа уравнений, необходимо использовать численные алгоритмы. Необходимо выделить из бесконечного множества решений одно, обоснованное математически решение. Эта проблема решается с посредством привлечения понятия нормального псевдорешения. Физический смысл заключается в том, что проведено m измерений с n неизвестными. Для того, чтобы получить единственное разумное решение, необходимо доопределить задачу, добавив априорную информацию о векторе х. Если подобная информация отсутствует, то решить систему невозможно. Следует ввести в задачу определённые ожидания о величине вектора х. Математически можно полагать вектор х нулевым, так как от любого вектора перейти к нулевому вектору можно линейным преобразованием. Таким образом, вполне логично объявить решением недоопределённой системы такое решение, которое ближе всех находится к нулевому вектору, т.е. обладает минимальной нормой |x|-min. Это решение называют нормальным псевдорешением системы Пример: Найти нормальное псевдорешение недоопределённый системы уравнений.
|
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-28; просмотров: 213; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.224.105 (0.006 с.) |

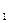 + 2x
+ 2x 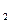 + x
+ x 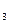 + 11x
+ 11x 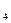 = 25
= 25 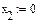

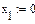
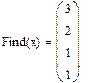
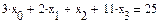
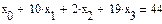


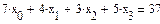
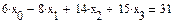
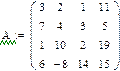
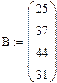

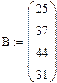 при символьном à
при символьном à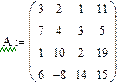

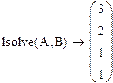
 Можно провести проверку:
Можно провести проверку: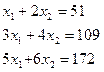 Попытаемся решить систему уравнений:
Попытаемся решить систему уравнений: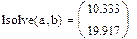
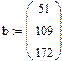
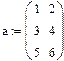
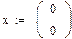
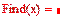
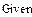
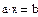
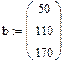
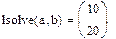
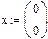
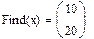
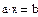
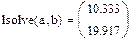
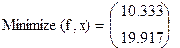
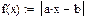
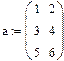 1-й способ:
1-й способ: