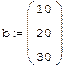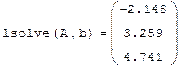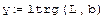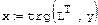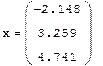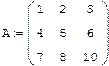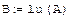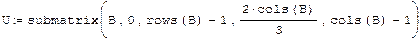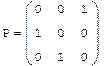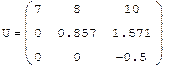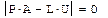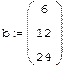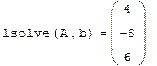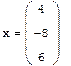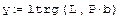Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вырожденные системы линейных уравненийСодержание книги
Поиск на нашем сайте
Вырожденная система- это система, описываемая матрицей с нулевым определителем (сингулярной матрицей). Плохо обусловленная система –определитель А не равен 0, но число обусловленности очень велико. Для решения таких систем разработан очень эффективный приём, называемый регуляризацией. Регуляризация Рассмотрим метод регуляризации, предложенный Тихоновым для решения обратных задач на примере линейной задачи. Как известно, она ставится в форме решения плохо обусловленной системы М линейных уравнений:
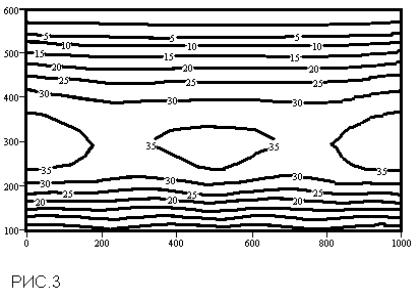
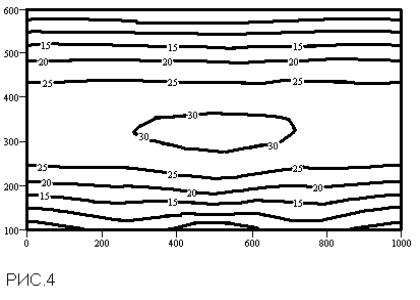
подобрать определенным способом. Покажем на конкретном примере задачи геофизической томографии, как решаются при помощи регуляризации линейные обратные задачи. Наиболее типичная постановка задачи томографии состоит в том, чтобы по набору измерений каждого из имеющихся приёмников в каждый момент времени измерений восстановить в узлах сетки, которой покрывается объект, поле пространственных переменных (которыми может быть, к примеру, температура в атмосфере или океане, скорость ветра и т.п.). Для окончательной формулировки вычислительной задачи необходимо записать систему линейных уравнений в дискретном виде.
Высота ИСЗ в компьютерном эксперименте составляла 900 км, два приёмника располагались в точках с координатами 0 км и 500 км по поверхности Земли в плоскости пролёта ИСЗ. Дискретизация интегральных уравнений проводилась методом кусочно-планарной аппроксимации на сетке 21х21 узел. Такая крупная (по сравнению с реальными задачами томографии атмосферы) сетка была взята нами для того, чтобы проверить выдвигаемую методику с помощью точного метода решения системы линейных уравнений (*), не прибегая к приближённым итерационным алгоритмам. Поскольку число арифметических операций, требующихся компьютеру для завершения точного метода, порядка (M)6, то для расчёта на сетке 100х100 узлов необходимо время в 15,000 раз большее. В скобках заметим, что на выполнение программы решения системы (*) методом Гаусса с выбором главного элемента занимает на Pentium-200 время порядка минуты, поэтому на практике следует, конечно, использовать итерационные методы. Эффективным может оказаться, например, метод сопряжённых градиентов, поскольку в его рамках можно организовать эффективный спуск по параметру регуляризации.
Пример: Дана вырожденная матрица. Найти её решения в зависимости от параметра регуляризации λ. При параметре регуляризации, равным 0, система не имеет решений. На первом этапе проводим регуляризацию матрицы. На втором выбираем оптимальное λ. Можно выбрать норму невязки, равной априорной оценке погрешностей задания исходных данных, либо использовать квазиоптимальный метод.
Матричные разложения При решении систем линейных уравнений с треугольной матрицей видно, что за минимальное число операций получен ответ. Поэтому удобно свести задачи решения систем общего вида к системам с треугольной матрицей. Пример: Решить систему с треугольной матрицей. (прямой ход) 1. Создадим пользовательскую функцию trg, используя элементы программирования. 2. Найдём корни и проведём проверку.
Разложение Холецкого Разложением Холецкого симметричной матрицы А является представление вида
где L- треугольная матрица. Алгоритм Холецкого реализован во встроенной функции cholesky.
Пример: Разложение Холецкого: 1. Ввести матрицу А 2. Записать разложение Холецкого 3. Получить матрицу L 4. Получить
Решение системы, если известно разложение, основано на замене исходной системы A*x=b другой системой L*y=b (где y=
LU - разложение Прямой ход алгоритма Гаусса можно записать в матричной форме: Такое представление матрицы А называют LU-разложением, или треугольным разложением. Lu(A)-LU-разложение матрицы. Результатом работы встроенной функции LU-разложения является матрица, составленная из матриц L и U соответственно. Чтобы выделить сами матрицы LU-разложения, а именно P,L,U необходимо применить функцию выделения подматрицы submatrix. Пример: Получим LU-разложение матрицы:
Пример: Решение системы при помощи LU- разложения:
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-28; просмотров: 324; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.41.252 (0.007 с.) |

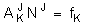 (1)
(1)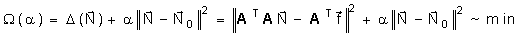 , (2)
, (2)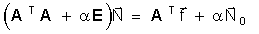 , (3)
, (3)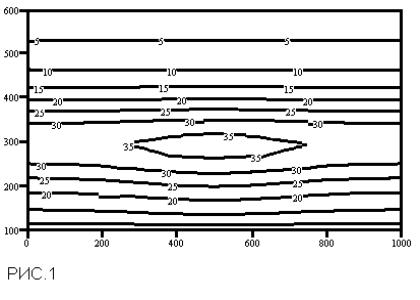

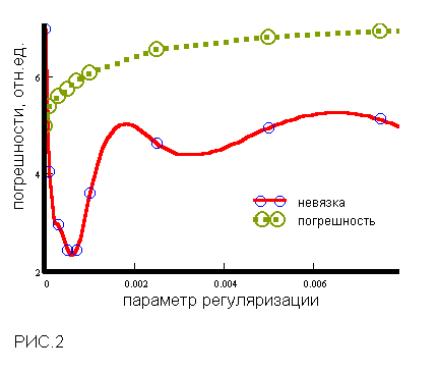



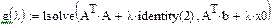

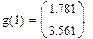


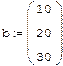

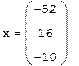
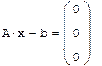
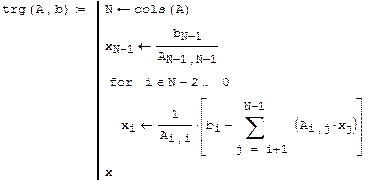
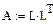
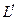


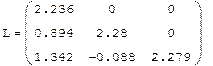
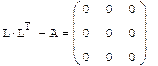

 *x).
*x).