
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциальные уравнения N -го порядка
Для решения ОДУ порядка N>=1 в Mathcad предусмотрены две возможности: · Вычислительный блок Given/Odesolve - в этом случае решение имеет вид функции от t; · Встроенные функции решения систем ОДУ, причём уравнениявысших порядков необходимо свести к эквивалентной системе уравнений первого порядка. В этом случае решение имеет формат вектора. Вычислительный блок для решения ОДУ, реализующий численный метод Рунга-Кутты, состоит из трёх частей: · Given-ключевое слово; · ОДУ и начальные условия в формате y(t0)=b записанные с помощью логических операторов, которые должны набираться на панели инструментов Boolean; · Odesolve(t,t1)-встроенная функция для решения ОДУ относительно переменной t на интервале (t0,t1), причём t0<t1.
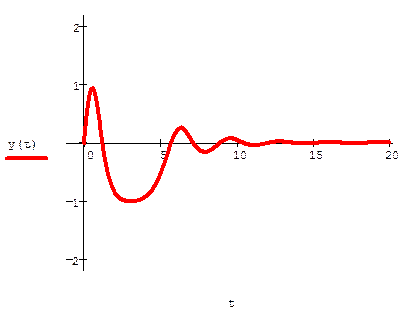
Пример: Решение задач Коши для ОДУ второго порядка (модель нелинейного осциллятора).
В примере можно применить различные модификации метода Рунга-Кутта. Для смены метода необходимо нажатием правой кнопки мыши на области функции Odesolve вызвать контекстное меню и выбрать в нём один из трёх пунктов: Fixed - (с фиксированным шагом); Adaptive- (Адаптивный); Stiff- (Для жёстких ОДУ). Схемы Рунге-Кутта Семейство схем Рунге-Кутта основано на аппроксимации неизвестных аргументов y(tn) в правых частях дифференциальных уравнений f(t,y).
В формуле
где
Если по различным причинам время расчетов становится критичным или точность неудовлетворительной, стоит попробовать вместо рассмотренного алгоритма Рунге-Кутта с фиксированным шагом другие методы. Например, если известно, что решение на рассматриваемом интервале меняется слабо, либо существуют участки медленных и быстрых его изменений, Метод Рунге-Кутта с переменным шагом основан на разбиении интервала не на равномерные шаги, а более оптимальным способом. Там, где решение меняется слабо, шаги выбираются более редкими, а в областях его сильных изменений - частыми. Это очень просто осуществить, т.к. алгоритм Рунге-Кутта является одношаговым и подразумевает простой пересчет при любом значении шага hn искомого y (tn+hn) через y (tn). Таким образом, легко обобщить алгоритм на адаптированный вариант, с выбором на каждом шаге своего hn в зависимости от локальной динамики решения на предыдущих шагах. В результате применения адаптированного алгоритма, для достижения одинаковой точности может потребоваться существенно меньшее число шагов, чем для стандартного алгоритма Рунге-Кутта с фиксированным шагом.
|
||||||||||||||
|
Последнее изменение этой страницы: 2020-11-28; просмотров: 54; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.6.75 (0.006 с.) |
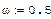
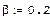
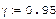
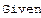
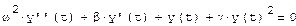
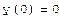

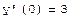
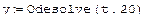

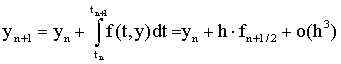 Рассмотрим идею этих методов на примере алгоритма 2-го порядка.
Рассмотрим идею этих методов на примере алгоритма 2-го порядка. 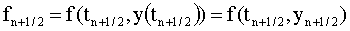
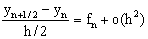
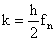
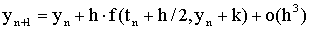

 В зависимости от выбора метода интегрирования ОДУ на элементарном шаге и конкретной формы аппроксимации y (t) в правой части ОДУ, получаются алгоритмы различной точности и быстродействия. Наиболее популярен алгоритм Рунге-Кутта четвертого порядка, описанный в большинстве книг по методам вычислений. Он обеспечивает малую погрешность для широкого класса систем ОДУ за исключением жестких систем и, при этом, довольно экономичен (на каждом шаге интегрирования требуется вычисление 4-х значений функции f):
В зависимости от выбора метода интегрирования ОДУ на элементарном шаге и конкретной формы аппроксимации y (t) в правой части ОДУ, получаются алгоритмы различной точности и быстродействия. Наиболее популярен алгоритм Рунге-Кутта четвертого порядка, описанный в большинстве книг по методам вычислений. Он обеспечивает малую погрешность для широкого класса систем ОДУ за исключением жестких систем и, при этом, довольно экономичен (на каждом шаге интегрирования требуется вычисление 4-х значений функции f):





