
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принцип программирования в MathcadСодержание книги
Поиск на нашем сайте
Основы вычислений Операторы численного и символьного вывода Для того чтобы выполнить простые расчёты по формулам, нужно выполнить: 1. Определить место для формулы 2. Ввести левую часть формулы 3. Ввести знак = или à В первом случае будет рассчитано численное выражение, а во втором аналитическое.
Пример: Вычислить Acos(0.5) через = и -à (Ctrl +.) Таким образом, можно выполнять и более сложные расчеты с использованием различных функций. Но это действия простого калькулятора с расширенным набором функций. Для инженерных расчётов представляет интерес возможность задания переменных и операций с функциями пользователя. В качестве оператора присваивания используется символ:= (на панели Калькулятор) х:=5 Пример: Определить функцию f(x)=x^2 + cos(x)+7 G(x,y,z)=x* asin(y)+cos(z) Для каждой из функций можно построить график:
1. Определить функцию 2. Вызвать панель для построения графиков 3. Выбрать нужный тип графика 4. В появившейся заготовке определить значения, которые будут отложены по осям.
Примечание: В Маthcad запрещено определять функции пользователя посредством рекуррентных выражений f(x)=f(x)+1 В этом случае будет организован бесконечный цикл, что приведёт к переполнению. При необходимости организовать рекуррентное вычисление нужно использовать новое имя функции.
Типы данных Кроме числовых действительных типов данных Маthcad оперирует и комплексными числами. Чтобы ввести комплексное число нужно: 1. Ввести действительную часть 2. Ввести действительный множитель 3. Ввести символ i или I после множителя.
Встроенные константы
Некоторые имена в Маthcad зарезервированы в системные переменные, которые называются встроенными константами. Встроенные константы делятся на два типа: математические, хранящие значения общепринятых математических символов, и системные, определяющие работу большинства численных алгоритмов.
Математические константы интерпретируются по-разному при численных и символьных вычислениях. Вычислительный процессор воспринимает их как числа, а символьный способен выдавать математические константы в качестве результата.
∞ ℮ π i, j –мнимые единицы % - 0.01
Системные переменные определяют работу численных методов, заложенных во встроенные функции. · TOL - точность численных методов · CTOL – точность выполнения выражений, используемая в некоторых численных методах · ORIGIN – номер начального индекса в массивах и строковых переменных · PRNPRECISION –установка формата данных при выводе в файл · PRNCOLWIDTH- установка формата столбца при выводе в файл · CWD – строковое представление пути к текущей рабочей папке.
ЗНАЧЕНИЯ:
Значением переменной или функции может быть не только число, но и строка, состоящая из любой последовательности символов. Для работы со строковыми переменными имеются несколько встроенных функций: concat(s1,s2,…) – слияние нескольких строк search(s,s1,n) –поиск подстроки в строке, начиная с заданной позиции strlen(s) - возвращает длину строки substr(s,m,n) - получает подстроку, выделением из строки n символов, начиная с позиции m.
Работа с массивами
Массивами называют упорядоченные последовательности чисел, или элементов массива. Доступ к любому элементу массива возможен по его индексу, т.е. по номеру в последовательности чисел. Применение массивов чрезвычайно эффективно в математических расчётах. В Mathcad условно выделяют два типа массивов · Векторы (одноиндексные), матрицы (двухиндексные) и тензоры (многоиндексные) · Ранжированные переменные – векторы, которые определённым образом зависят от их индекса.
Пример: 1. Ввести имя матрицы 2. Поставить оператор присваивания 3. Панель инструментов Matrix 4. Выбрать матрицу, задать количество столбцов и строк
Номер строки и столбца вводится через запятую. Доступ ко всему массиву осуществляется обычным поименованием векторной переменной. Над элементами массива можно выполнять такие же действия, как над обычными числами.
Размерные переменные
В Mathcad числовые переменные и функции могут обладать размерностью. Сделано это для упрощения инженерных и физических расчётов. В Mathcad встроено большое количество единиц измерения, с помощью которых и создаются размерные переменные. Примеры: Сила тока в амперах
Программирование в Mathcad
Основными инструментами работы в Mathcad являются математические выражения, переменные и функции. Нередко записать формулу, использующую ту или иную внутреннюю логику, в одну строку не удаётся. В этом случае удобно использовать программные модули.
Алгебраические вычисления Операторы
Каждый оператор в Mathcad обозначает некоторое математическое действие в виде символа. Ряд действий в полном согласии с математической терминологией (сложение, вычитание, деление, транспонирование матриц и т.п.) реализован в виде встроенных операторов, а другие действия в виде встроенных функций. Арифметические операторы Операторы, обозначающие основные арифметические действия, вводятся с панели Calculator.
Вычислительные операторы
Вычислительные операторы вставляются в документы при помощи панели инструментов Calculus. При нажатии любой из кнопок появляется символ соответствующего математического действия, снабжённый несколькими местозаполнителями. Количество и расположение местозаполнителей определяется типом оператора и в точности соответствует общепринятой математической модели.
Пример: Вычисление определённого интеграла.
Необходимо было заполнить границы интегрирования, подынтегральную функцию. Пример:
Логические операторы
Результатом вычисления логических операторов есть 1-если логическое выражение верно, либо – 0, если нет.
Пример: Проверить x равно y. 1. Ввести х=5 2. Ввести у=5 3. Вставить с панели Boolean соответствующий оператор = 4. В появившихся местозаполнителях поставить х и у. 5. Нажать клавишу =, чтобы получить ответ.
Матричные операторы
Матричные операторы предназначены для совершения различных действий над векторами и матрицами. В основном они используются при реализации алгоритмов линейной алгебры. Существуют несколько способов создания векторов и матриц: 1. Нажать кнопку Matrix or Vector на панели Matrix, либо клавиши Ctrl + M, или выбрать пункт меню Insert Matrix. 2. В диалоговом окне Insert Matrix задать целое число столбцов и строк матрицы, которую нужно создать. 3. Нажать кнопку OK или Insert в результате в документ будет вставлена заготовка матрицы с определённым числом строк и столбцов. 4. Ввести значения в местозаполнители элементов матрицы.
Операторы выражения
Вычислительные операторы сгруппированы на панели Evaluation · Численный вывод =; · Символьный (аналитический) -->; · Присваивание:=; ·
Функции
Mathcad содержит огромное количество встроенных функций.
Некоторые из них просто рассчитывают определённое значение, а некоторые реализуют сложные численные алгоритмы.
Элементарные функции
· Exponential and logarithmic functions- логарифмы и экспонента · Complex - комплексные · Trigonometric - тригонометрические · Inverse trig -обратные тригонометрические · Hyperbolic - гиперболические · Inverse hyperbolic - обратные гиперболические · Sinc - Sinc-функция
Пример: Рассчитать тригонометрические функции:
Пример: Рассчитать логарифмические функции
Вспомогательные функции
Кроме перечисленных Mathcad включает целый ряд вспомогательных функций. · Разрывные функции · Сокращения и округления · Сортировка · Финансовые · Преобразования координат · Условия · Типа выражения
Пример:
Ceil(3.7)=4 flooar(3.7)=3 round(1.23445,0)=1 round(1.2345,1)=1.2
Вычисление предела
Наиболее ярким проявлением возможностей символьного процессора являются аналитические вычисления пределов, производных, интегралов и разложений в ряд, а также решение алгебраических уравнений. Все эти операции, при выполнении их посредством меню Symbolics находятся в подменю Variable.
Примечание: В отличие от других вычислительных процессов пределы могут быть вычислены только лишь символьно. Пример: Вычислить пределы некоторых функций. 1. Установить знак символьного вывода 2. Слева записать предел 3. Заполнить все местозаполнители
Дифференцирование Операция дифференцирования реализована как в численной, так и в аналитической форме и обозначается при помощи традиционного оператора
Производные высших порядков
Mathcad определяет производные высших порядков от 0 до 5 включительно. Чтобы вычислить производную функции f(x) n-порядка, нужно определить те же самые действия, что и при взятии первой производной, за тем исключением, что вместо оператора производной нужно применить оператор n-й производной Линейная алгебра
Задачи линейной алгебры делятся на два класса. Первый – это простейшие матричные операции. Второй класс – это более сложные действия, которые реализуют алгоритмы вычислительной линейной алгебры (вычисление определителей, вычисление собственных векторов и собственных значений, решение систем линейных алгебраических уравнений и различные матричные разложения.
Транспонирование Транспонированием матрицы называют операцию, переводящую матрицу размерности N x M в матрицу M x N. 1. Ввести через оператор присваивания матрицу 2. Установить знак = 3. Слева символ транспонирования матрицы с панели инструментов 4. Справа будет выведен результат.
Сложение и вычитание матриц В Мathcad можно складывать или вычитать матрицы их друг из друга, используя стандартные символы + или -. Матрицы должны иметь одинаковую размерность.
Для вычисления суммы всех элементов вектора или матрицы существует вспомогательный оператор, задаваемый кнопкой Vector Sum. 1. Установить оператор символьного вывода à 2. Cлева установить оператор Vector Sum 3.
Сумма диагональных элементов квадратной матрицы называется следом матрицы. В Мathcad данная операция организована в виде встроенной функции tr. 1. Установить оператор символьного вывода à 2. Cлева написать функцию tr.
Умножение матриц При умножении матриц нужно помнить о том, что матрицу размерности M x N можно умножить только лишь на матрицу размерности N x P, причём M и P могут быть произвольными. 1. Ввести две матрицы 2. Установить оператор символьного вывода à 3. Слева написать а*в 4. Справа появится результат
Векторная алгебра Векторы являются частным случаем, поэтому для них справедливы все те операции, что и для матриц. Но есть и специфические операторы. Модуль вектора
квадратов его элементов. 1. Установить оператор символьного вывода à 2. Слева поставить модуль, ввести вектор 3. Справа результат
Скалярное произведение Скалярное произведение определяется как скаляр, равный сумме попарных произведений соответствующих элементов. Векторы должны иметь одинаковую размерность, скалярное произведение имеет ту же размерность. Установить знак умножения Векторное произведение
Заполнить местозаполнители. Определитель квадратной матрицы Определитель в Mathcad обозначается традиционно стандартным математическим символом. Чтобы ввести оператор нахождения определителя матрицы, можно нажать кнопку Determinat на панели инструментов Matrix или набрать на клавиатуре | |, нажав клавиши Ctrl + <\>. 1. 2. Установить | |. Ввести матрицу. Ранг матрицы
Рангом матрицы называют наибольшее натуральное число k, для которого существует не равный нулю определитель k-порядка подматрицы, составленной из любого пересечения k столбцов и k строк матрицы. Для вычисления ранга матрицы в Mathcad предназначена функция rank.
Обращение квадратной матрицы
Поиск обратной матрицы возможен, если матрица квадратная и её определитель не равен нулю. Произведение исходной матрицы на обратную по определению является единичной матрицей. Для ввода оператора поиска обратной матрицы нажать кнопку Inverse (Обратная матрица) на панели инструментов Matrix. 1. Установить знак =. 2. Слева нажать кнопку Inverse и ввести матрицу. 3. Справа появится обратная матрица.
Сортировка элементов матрицы Элементы матрицы можно отсортировать по возрастанию или убыванию. Для этого имеются несколько встроенных функций, которые позволяют гибко управлять сортировкой матриц. · sort(v)-сортировка элементов вектора в порядке возрастания. · reverse(v)-перестановка элементов вектора в обратном порядке · csort(A,i) –сортировка i -столбца по возрастанию · rsort(A,i) –сортировка i - строки по возрастанию
Сортировка вектора
Сортировка матриц по строке и столбцу
Вывод размера матрицы Для получения сведений о характеристиках матриц или векторов предусмотрены следующие встроенные функции: · rows(A)-число строк. · cols(A) – число столбцов. · length(v) – число элементов вектора. · last(v) – индекс последнего элемента вектора.
Численное решение уравнений Отыскание корней алгебраического уравнения численными методами связано с двумя задачами: · Локализация корней, т.е. определение их существования, количества, примерного расположения. · Отыскание корней с заданной точностью, т.е. найти корни, при которых значение функции отличается от 0 не более, чем на TOL. Для численного решения систем уравнений применяется тот же самый вычислительный блок, что и для символьных вычислений. При численных вычислениях может быть найден только один из корней уравнения. Отличия численного нахождения корней от символьного: 1. Вместо оператора символьного вывода используется оператор численного вывода (=). 2. Перед вычислительным блоком должны быть заданы начальные значения для всех неизвестных.
Системы линейных уравнений Центральным вопросом вычислительной линейной алгебры является решение систем линейных алгебраических уравнений (СЛАУ), т. е. систем уравнений вида К системам линейных уравнений сводится множество, если не сказать большинство, задач вычислительной математики. СЛАУ имеет единственное решение, если матрица A является невырожденной, или по-другому, несингулярной, т. е. ее определитель не равен нулю. С вычислительной точки зрения, решение СЛАУ не представляет трудностей, если матрица A не очень велика. С большой матрицей проблем также не возникнет, если она не очень плохо обусловлена. Алгоритм исключения Гаусса Алгоритм последовательных исключений Гаусса основан на преобразовании матрицы A линейной системы Ax = b к треугольному виду (т.е. к форме, когда все элементы ниже главной диагонали матрицы являются нулевыми). Точнее, СЛАУ Ax = b заменяется эквивалентной системой с другой матрицей A* и другим вектором правых частей b*, но имеющей то же решение, что и исходная система. Алгоритм состоит в следующем: 1. Проводится прямой ход исключения неизвестных путем подстановки одних уравнений в другие. Используются следующие формулы: 2. При помощи обратного хода определяются все неизвестные х. Для этого хN сразу определяется из последнего уравнения, в которое не входят другие х (матрица системы теперь является трехдиагональной). Затем хN подставляется в предыдущее уравнение, из которого сразу определяется хN-1 и т.д. Этот метод реализован во встроенной функции lsolve. При использовании этого метода система уравнений должна быть записана в матричной форме. Алгоритм выполнения: 1. Ввести матрицу с коэффициентами при неизвестных 2. Ввести столбец свободных членов 3. Записать функция lsolve 4. При численном решении после функции ставится знак =, а
Переопределённые системы Рассмотрим систему уравнений, в которой число уравнений больше, чем число неизвестных, т.е. матрица А – прямоугольная. Чаще всего такие системы не имеют решений, т.е. являются несовместными или переопределёнными. Несовместные системы не могут быть решены с помощью вычислительного блока Given/Find. Пример:
1. Через оператор присваивания вводим матрицу коэффициентов и вектор свободных членов. 2. Решаем данную систему методом Гаусса 3. Вводим приблизительные решения корней в вектор х 4. Включаем вычислительный блок 5. Записываем а*х=в 6. Находим корни Find(x)= 7. Mathcad выдаст ошибку.
В редких случаях система с прямоугольной матрицей может оказаться совместной (если выбран соответствующий вектор b).
На практике задачи отыскания решения переопределённых систем линейных уравнений встречаются довольно часто. Точного решения такой системы не найти. Рассмотрим математическую постановку задач решения систем с прямоугольной матрицей. Вместо точного решения следует организовать поиск такого вектора х, который будет наилучшим образом удовлетворять всем уравнениям, т.е. минимизировать их невязку (расхождение между вектором А*х и вектором свободных членов b). Так как невязка A*x-b является векторной величиной, то минимизации надо подвергать её норму (т.е. скаляр) |A*x-b|. Т.е. принято искать не точное решение (которого просто нет), а псевдорешение-вектор, минимизирующий норму невязки системы уравнений. Задача решения линейной системы уравнения заменяется задачей отыскания глобального минимума функции f(x)=|A*x-b|. Поскольку эта минимизируемая норма зависит от суммы квадратов компонент неизвестного вектора, то процедура поиска псевдорешения является реализацией метода наименьших квадратов. Для решения задач минимизации невязки системы уравнений в Mathcad предусмотрены две встроенные функции Minerr и Minimize. Если используется функция Minerr, то используется ключевое слово Given, а в первом случае явно определяется функция f(x), подлежащая минимизации.
2-й способ:
Во-первых, сравнивая результаты, можно обнаружить, что они абсолютно различны, причём более похож на правильный ответ, выдаваемый функцией Minimize. Разгадка заключается в особенностях применения численного алгоритма, заложенного в функцию MinErr. Алгоритм заложен линейный, тип алгоритма можно изменить по правой кнопке мыши. Установить на нелинейный, выбрать метод из трёх предложенных. Во-вторых, приближённое решение c использованием Given невозможно при наличии дополнительных условий, выражающих вспомогательную априорную информацию о постановке задачи. В результате исходная задача сводится к условной минимизации функции f(x) c использованием дополнительных неравенств.
Пример: Поиск псевдорешения при наличии априорной информации
При выборе нелинейного алгоритма появляются отрицательные ответы, а при добавлении дополнительных условий в задачу решения ещё раз меняются.
Недоопределённые системы Рассмотрим системы с количеством уравнений меньшим количества неизвестных. Такие системы имеют либо бесконечное множество решений, либо не имеют решения вовсе. Решим аналитически систему двух уравнений с тремя неизвестными при помощи символьного процессора.
Но для решения недоопределённых систем, состоящих из большего числа уравнений, необходимо использовать численные алгоритмы. Необходимо выделить из бесконечного множества решений одно, обоснованное математически решение. Эта проблема решается с посредством привлечения понятия нормального псевдорешения. Физический смысл заключается в том, что проведено m измерений с n неизвестными. Для того, чтобы получить единственное разумное решение, необходимо доопределить задачу, добавив априорную информацию о векторе х. Если подобная информация отсутствует, то решить систему невозможно. Следует ввести в задачу определённые ожидания о величине вектора х. Математически можно полагать вектор х нулевым, так как от любого вектора перейти к нулевому вектору можно линейным преобразованием. Таким образом, вполне логично объявить решением недоопределённой системы такое решение, которое ближе всех находится к нулевому вектору, т.е. обладает минимальной нормой |x|-min. Это решение называют нормальным псевдорешением системы Пример: Найти нормальное псевдорешение недоопределённый системы уравнений.
Регуляризация Рассмотрим метод регуляризации, предложенный Тихоновым для решения обратных задач на примере линейной задачи. Как известно, она ставится в форме решения плохо обусловленной системы М линейных уравнений:
подобрать определенным способом.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-28; просмотров: 156; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.120.103 (0.012 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

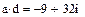
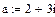
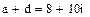
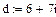
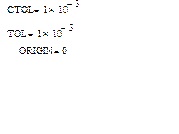
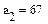
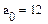
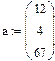
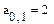 Индекс вводится также с панели инструментов Matrix или через знак [ на клавиатуре.
Индекс вводится также с панели инструментов Matrix или через знак [ на клавиатуре.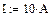
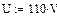 Напряжение
Напряжение 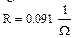 Сопротивление
Сопротивление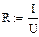
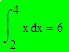
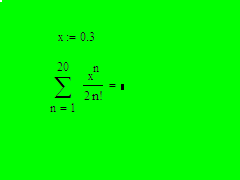 Вычислить сумму ряда
Вычислить сумму ряда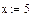
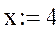
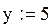
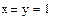
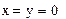
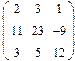

 Глобальное присваивание
Глобальное присваивание 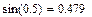
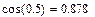
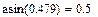
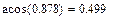
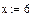
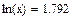

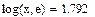
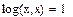
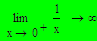
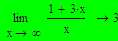
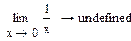
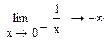
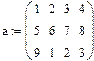

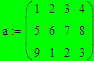
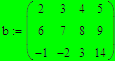
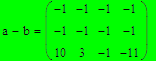
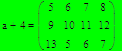

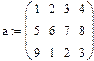 Справа появится результат.
Справа появится результат.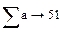
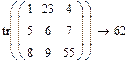 3. Справа появится результат.
3. Справа появится результат.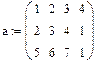
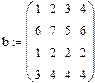

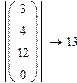 Модуль вектора по определению равен квадратному корню из суммы
Модуль вектора по определению равен квадратному корню из суммы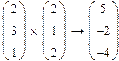 Векторное произведение двух векторов u и v с углом σ между ними равно вектору с модулем |u|*|v|*sinσ, направленным перпендикулярно плоскости векторов u и v. Обозначают векторное произведение символом «х», который можно ввести нажатием кнопки Cross Product (векторное произведение) в панели Matrix (Матрица) или сочетанием клавиш <Ctrl>+<8>.
Векторное произведение двух векторов u и v с углом σ между ними равно вектору с модулем |u|*|v|*sinσ, направленным перпендикулярно плоскости векторов u и v. Обозначают векторное произведение символом «х», который можно ввести нажатием кнопки Cross Product (векторное произведение) в панели Matrix (Матрица) или сочетанием клавиш <Ctrl>+<8>.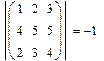 Поставить знак =
Поставить знак =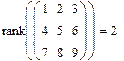
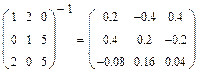
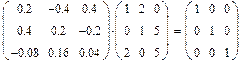
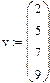
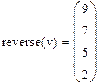
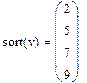
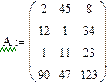
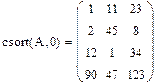
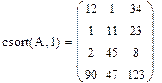
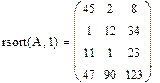
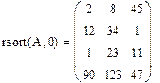
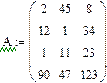
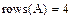
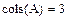
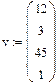
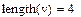
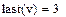
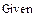
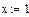 Пример:
Пример: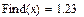
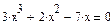 Решение кубического уравнения
Решение кубического уравнения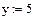 Решение системы из двух уравнений
Решение системы из двух уравнений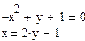
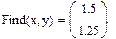
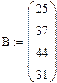 при символьном à
при символьном à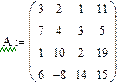

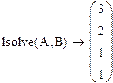
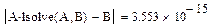 Можно провести проверку:
Можно провести проверку: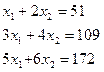 Попытаемся решить систему уравнений:
Попытаемся решить систему уравнений: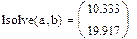
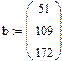
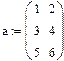
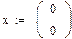
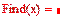
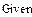
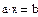
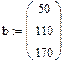
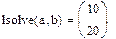
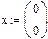
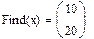
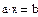
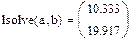
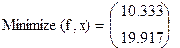
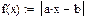
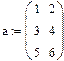 1-й способ:
1-й способ: 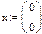
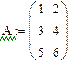
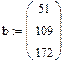
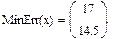
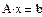
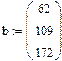
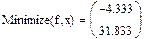
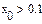
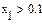
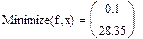
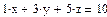
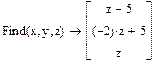
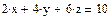
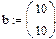
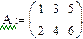
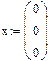
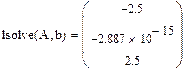
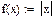
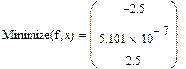
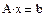
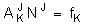 (1)
(1)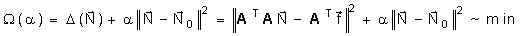 , (2)
, (2)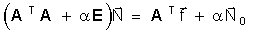 , (3)
, (3)


