
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обыкновенные дифференциальные уравненияСодержание книги
Поиск на нашем сайте
Дифференциальные уравнения являются разновидностью математических моделей, описывающих природные и технологические процессы. Дифференциальные уравнения - это уравнения, в которых неизвестными являются не переменные (т. е. числа), а функции одной или нескольких переменных. Эти уравнения (или системы) включают соотношения между искомыми функциями и их производными. Если в уравнения входят производные только по одной переменной, то они называются обыкновенными дифференциальными уравнениями (сокращение ОДУ). В противном случае говорят об уравнениях в производных. Таким образом, решить (иногда употребляют другое слово проинтегрировать) дифференциальное уравнение -значит определить неизвестную функцию на определенном интервале изменения ее переменных. Как известно, одно обыкновенное дифференциальное уравнение или система ОДУ имеет единственное решение, если помимо уравнения определенным образом заданы начальные или граничные условия. Имеются два типа задач: Как правило, решение задач Коши для ОДУ и их систем - задача, хорошо разработанная и с вычислительной точки зрения не слишком сложная. Большое значение здесь имеет представление результатов и анализ зависимостей решения от различных параметров системы. Между тем, имеется целый класс ОДУ, называемых жесткими, который не поддается решению стандартными методами, типа методов Рунге-Кутта. Для них имеются специальные алгоритмы. Задачи Коши для ОДУ ОДУ первого порядка может по определению содержать помимо самой искомой функции y(t) только ее первую производную y'(t). В подавляющем большинстве случаев дифференциальное уравнение можно записать в стандартной форме (форме Коши): y'(t)=f(y(t),t).
Задача Коши для системы - решить ОДУ с начальным условием y(0)= C. Искомая функция y(t) может быть вектором, т.е. включать несколько (L) неизвестных функций y1(t),..., yL(t). Тогда, соответственно, должно быть поставлено L начальных условий. Стандартные процедуры Mathcad применимы для систем ОДУ первого порядка. Но если в систему входят и уравнения высших порядков, то её можно свести к системе большего числа уравнений первого порядка. Пример: Рассмотрим уравнение второго порядка модели осциллятора. Модель гармонического осциллятора описывает, в частности, колебания маятника: y(t) описывает изменения угла его отклонения от вертикали; y'(t)-угловую скорость маятника;
Примечание: Символ производной набирается с помощью сочетания клавиш <Ctrl>+<F7>.
Модели, основанные на задачах Коши для ОДУ, часто называют динамическими системами. Они содержат производную по времени t и описывают динамику некоторых параметров. Для изучения динамических систем центральным моментом является анализ фазовых портретов, т.е. решений, получающихся при выборе всевозможных начальных условий.
|
|||||||||||
|
Последнее изменение этой страницы: 2020-11-28; просмотров: 100; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.183.161 (0.005 с.) |

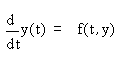
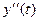 -ускорение, а начальные условия, соответственно, начальное отклонение маятника y(0)=1.0 и начальную скорость y'(0)=0. Модель является линейной.(модель затухающего гармонического осциллятора).
-ускорение, а начальные условия, соответственно, начальное отклонение маятника y(0)=1.0 и начальную скорость y'(0)=0. Модель является линейной.(модель затухающего гармонического осциллятора).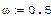
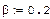
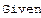
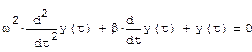
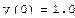
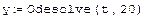
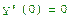
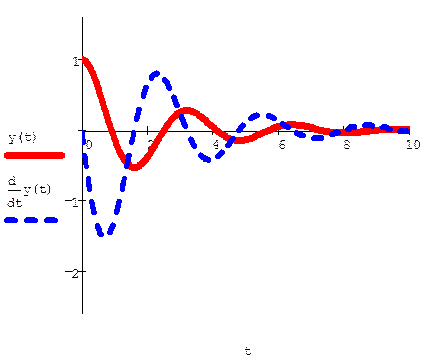
 Решение ОДУ удобнее изображать в фазовом пространстве, по каждой из осей которого откладываются значения каждой из найденных функций. При таком построении графика аргумент t будет присутствовать на нём лишь параметрически. Фазовое пространство является координатная плоскость, а решение представляет собой кривую, или по-другому, траекторию, выходящую из точки, координаты которой равны начальным условиям.
Решение ОДУ удобнее изображать в фазовом пространстве, по каждой из осей которого откладываются значения каждой из найденных функций. При таком построении графика аргумент t будет присутствовать на нём лишь параметрически. Фазовое пространство является координатная плоскость, а решение представляет собой кривую, или по-другому, траекторию, выходящую из точки, координаты которой равны начальным условиям.


