Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Таблична модель поведінки клієнта страхової компаніїСодержание книги
Поиск на нашем сайте Нехай клієнт страхової компанії є власником певного активу (майно, внесок у банк, людський капітал), величина якого виражається у грошовій формі. Величину активу будемо позначати через А Можливий страховий випадок, коли клієнт втрачає актив або його частку. Це може бути у випадку стихійного лиха, пограбування, банкрутства фінансової установи, якій клієнт довірив свій актив, несприятливої кон'юнктури ринку, втрати працездатності внаслідок виробничої або побутової травми. Будемо розглядати спрощений випадок, коли актив або повністю недоторканий, або повністю вилучений. Припускається, що клієнт може оцінити імовірність страхового випадку. Позначатимемо її через π; Для того щоб бути більш певним у своєму майбутньому, власник активу може звернутись до страхової компанії й застрахувати актив або його частку. Компанія пропонує такі умови страхування: 1) клієнт сплачує компанії страховий внесок, пропорційний частці страхованого активу. Позначимо через r питомий страховий внесок, або ціну страхування, тобто страховий внесок, що припадає на одиницю страхованого активу; 2) якщо трапляється страховий випадок, компанія сплачує клієнтові страхову винагороду, яка теж пропорційна частці застрахованого активу Через q будемо позначати питому страхову винагороду, тобто страхову винагороду, що припадає на одиницю застрахованого активу. Аналіз взаємодії страхової компанії та її клієнтів буде здійснений за таких припущень щодо їх поведінки: 1) Клієнт залежно від питомого страхового внеску та питомої страхової винагороди обирає частку страхованого активу. 2) Клієнт є несхильним до ризику, тобто для нього більш привабливим є отримання гарантованого сподіваного виграшу, ніж участь у ризикованій акції, яка має такий самий сподіваний ефект. Припущення можна перефразувати в більш звичних термінах для страхової справи. Наприклад, власник будинку вартістю 400000 гривень може його втратити внаслідок стихійного лиха, імовірність якого становить 0,0001 на рік. Сподіваний програш становить у цьому випадку 400000 × 0.0001 = 40. Проте власник будинку залюбки буде сплачувати 100, а то й 200 гривень щороку страховій компанії, аби вона йому гарантувала відшкодування вартості будинку. 3) Моделлю системи цінностей людини, яка не байдужа до ризику, є сподівана корисність. Чим більша сподівана корисність для людини, тим більш комфортно вона себе почуває. 4) Також будемо припускати, що функція корисності за Нейманом-Моргенштерном клієнта є монотонно зростаючою.
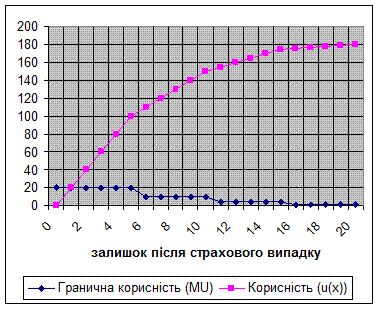
Числовий приклад Величина активу становить 20000 гривень. Власник активу – особа, несхильна до ризику. Гранична корисність для власника активу задається формулою:
де інтервали зміни величини активу вказані в тисячах. Імовірність страхового випадку π= 0, 0001. Питомий страховий платіж (надалі будемо його називати просто страховим платежем) r =0, 001, питома страхова винагорода q =1. Іншими словами, кожна застрахована 1000 відшкодовується повністю у разі страхового випадку, але для цього клієнт повинен сплатити компанії 1 гривню. Чи буде власник активу страхуватись взагалі, а якщо буде, то яким обсягом? Насамперед кілька зауважень щодо системи цінностей потенційного клієнта. Найбільш вагомою для нього буде втрата останніх одиниць його активу (кожна одиниця серед останніх п'яти важить 20 ютилів). Далі вагомість втрати зменшується. В Табл. 1 (с???) наведена корисність багатства потенційного клієнта. Рис 1 (с. 141) є графічним відображенням Табл. 1
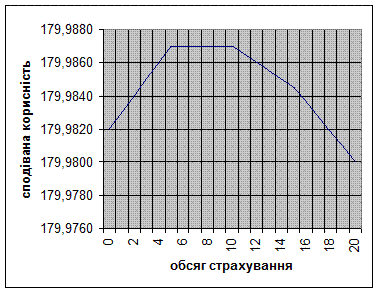
Очевидно, що функція корисності клієнта є увігнутою, тобто він несхильний до ризику. Для нього найбільш вагомими є останні одиниці втрати активу після страхового випадку. Порівняємо добробут клієнта за відсутності страхування та у випадку, коли він страхує перші одиниці активу. Якщо клієнт не страхується зовсім, то він матиме, як і раніше, актив обсягом 20000 за відсутності страхового випадку, та нічого, якщо страховий випадок трапиться. З точки зору корисності, він матиме 180 ютилів (див. Табл.?, с. 140) з імовірною 0,9999 та нуль з імовірністю 0,0001. Сподівана корисність становитиме: 0, 9999 × 180 + 0, 0001 × 0= 1 79, 9 8 2. Якщо клієнт страхує 4 тисячі, то у разі відсутності страхового випадку у нього залишиться: 20000 - 4000×0, 001 = 19,996, а у разі страхового випадку ‑ 4000 гривень. Корисність першої суми, згідно з Табл.?? (с 140), становитиме 179,996, другої ‑ 80. Звідси, сподівана корисність дорівнюватиме: 179, 996 × 0.9999 + 80 × 0, 0001 = 179, 9 8 6. Таким чином, для особи з функцією корисності, яка відображена в Табл.??? та на Рис.???, страхування обсягом 4 тисячі є більш привабливим порівняно з випадком, коли особа взагалі не страхується. У Табл.?? (с. 140) та на Рис??? (с.???) відображені результати аналогічних розрахунків для всіх можливих варіантів страхування з кроком 1000. Здійснені розрахунки показують, що діапазон від 5 до 10 тисяч містить найпривабливіші обсяги страхування для клієнта.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-22; просмотров: 171; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.009 с.) |

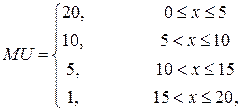 (?)
(?)