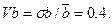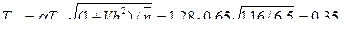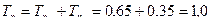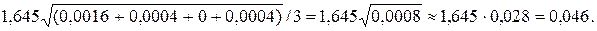Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сутність, особливості і завдання актуарних розрахунківСодержание книги
Поиск на нашем сайте
ОСНОВИ ТАРИФНИХ РОЗРАХУНКІВ З РИЗИКОВИХ ВИДІВ СТРАХУВАННЯ
ВИЗНАЧЕННЯ ТАРИФНОЇ НЕТТО-СТАВКИ З ДІЮЧИХ РИЗИКОВИХ ВИДІВ СТРАХУВАННЯ Отримана оцінка збитковості для 5-го року може бути прийнята за основну частину нетто-ставки. Розрахунок ризикової надбавки ( 1) Знаходяться відхилення фактичних значень збитковості в окремі роки від отриманих при розрахунку основної частини нетто-ставки теоретичних (вирівняних) її значень для цих років. У нашому прикладі ці відхилення становитимуть, грн: 0,28-0,254=+0,026; 0,30-0,326=-0,026; 0,37-0,398=-0,028; 0,50-0,470=+0,030; 0,54-0,542=-0,002. 2) Кожне знайдене відхилення підноситься до квадрату: (0,026) (-0,026) (-0,028) (0,030) (-0,002) 3) Квадрати відхилень підсумовуються і діляться на число відхилень мінус 1:
4) Із середнього квадрату відхилень добувається квадратний корінь:
Таким чином, ризикова надбавка у розглянутому прикладі становить 0,03 грн із 100 грн страхової суми.
Числовий приклад Величина активу становить 20000 гривень. Власник активу – особа, несхильна до ризику. Гранична корисність для власника активу задається формулою:
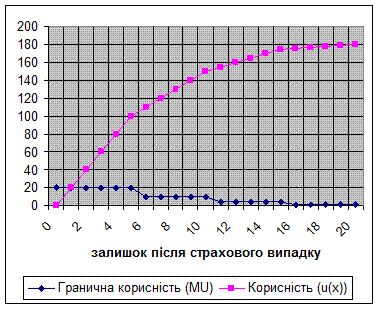
де інтервали зміни величини активу вказані в тисячах. Імовірність страхового випадку π= 0, 0001. Питомий страховий платіж (надалі будемо його називати просто страховим платежем) r =0, 001, питома страхова винагорода q =1. Іншими словами, кожна застрахована 1000 відшкодовується повністю у разі страхового випадку, але для цього клієнт повинен сплатити компанії 1 гривню. Чи буде власник активу страхуватись взагалі, а якщо буде, то яким обсягом? Насамперед кілька зауважень щодо системи цінностей потенційного клієнта. Найбільш вагомою для нього буде втрата останніх одиниць його активу (кожна одиниця серед останніх п'яти важить 20 ютилів). Далі вагомість втрати зменшується. В Табл. 1 (с???) наведена корисність багатства потенційного клієнта. Рис 1 (с. 141) є графічним відображенням Табл. 1
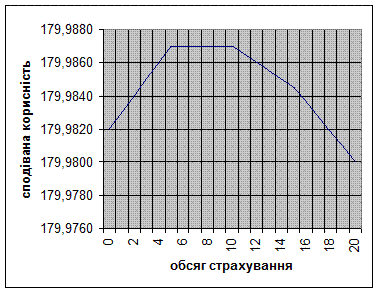
Очевидно, що функція корисності клієнта є увігнутою, тобто він несхильний до ризику. Для нього найбільш вагомими є останні одиниці втрати активу після страхового випадку. Порівняємо добробут клієнта за відсутності страхування та у випадку, коли він страхує перші одиниці активу. Якщо клієнт не страхується зовсім, то він матиме, як і раніше, актив обсягом 20000 за відсутності страхового випадку, та нічого, якщо страховий випадок трапиться. З точки зору корисності, він матиме 180 ютилів (див. Табл.?, с. 140) з імовірною 0,9999 та нуль з імовірністю 0,0001. Сподівана корисність становитиме: 0, 9999 × 180 + 0, 0001 × 0= 1 79, 9 8 2. Якщо клієнт страхує 4 тисячі, то у разі відсутності страхового випадку у нього залишиться: 20000 - 4000×0, 001 = 19,996, а у разі страхового випадку ‑ 4000 гривень. Корисність першої суми, згідно з Табл.?? (с 140), становитиме 179,996, другої ‑ 80. Звідси, сподівана корисність дорівнюватиме: 179, 996 × 0.9999 + 80 × 0, 0001 = 179, 9 8 6. Таким чином, для особи з функцією корисності, яка відображена в Табл.??? та на Рис.???, страхування обсягом 4 тисячі є більш привабливим порівняно з випадком, коли особа взагалі не страхується. У Табл.?? (с. 140) та на Рис??? (с.???) відображені результати аналогічних розрахунків для всіх можливих варіантів страхування з кроком 1000. Здійснені розрахунки показують, що діапазон від 5 до 10 тисяч містить найпривабливіші обсяги страхування для клієнта. Теорема про рівновагу Теорема 1 Припустимо, клієнт ‑ несхильний до ризику й має монотонно зростаючу та диференційовану функцію корисності. У цьому разі,
то клієнт ухиляється від страхування, якщо
то клієнт страхує весь актив; якщо ж
то клієнт страхує частку свого активу (але не весь актив), причому для обсягу страхування, який забезпечує максимальну сподівану корисність х*, виконується:
Доведення Оскільки клієнт несхильний до ризику, то його функція корисності увігнута. Доведення базується на властивостях увігнутих функцій. Дійсно, з властивостей увігнутих функцій з увігнутості функції корисності и(х) випливає увігнутість функції сподіваної корисності u (x). Звідси, гранична сподівана корисність U '(x) спадає у разі зростання обсягу страхування. Отже, максимальна гранична сподівана корисність буде спостерігатись у точці 0. За максимального обсягу страхування гранична сподівана корисність буде мінімальною. Таким чином, можна виписати співвідношення для задачі (1):
Оскільки, то
Сполучаючи останні три співвідношення з (2'), (3'), (4') отримуємо доведення теореми про рівновагу.
Аналіз рівноваги Рівняння (5) допускає таке читання: в стані рівноваги гранична корисність страхування за наявності страхового випадку, перемножена на його імовірність, збігається з граничною шкодою від страхування за відсутності страхового випадку, перемноженою на його імовірність. Отже, клієнт балансує граничну шкоду та граничну корисність для визначення найбільш привабливого для себе обсягу страхування, причому, враховуючи імовірність страхового випадку. Нерівність (2) можна переписати таким чином:
тобто, якщо гранична шкода першої одиниці страхування за відсутності страхового випадку, перемножена на імовірність недоторканості активу, перевищує граничну корисність останньої одиниці активу за умови, що страховий випадок трапився, перемножену на його імовірність, то клієнт не схильний до страхування в будь-яких обсягах. Аналогічну інтерпретацію можна дати й для нерівності (3), коли переписати її у вигляд
маючи на увазі, що величина u '((1- r) A) r характеризує граничну шкоду від страхування за максимально можливого його обсягу за умови недоторканості активу, a u '(qA) q ‑ граничну корисність максимально можливого обсягу страхування за умови, коли трапляється страховий випадок. Звернемось ще раз до рівняння рівноваги (5), для того щоб помітити цікаву деталь: оскільки здебільшого імовірність недоторканості активу 1-πістотно більша імовірності страхового випадку π, то гранична корисність страхування за умови страхового випадку повинна бути набагато більшою від граничної шкоди від страхування за умови, коли страховий випадок не трапляється. Модель страхової компанії Очевидно, що сподівана корисність прибутку компанії залежить від параметрів страхування r, q. Її метою є підбір параметрів страхування таким чином, щоб максимізувати сподівану корисність прибутку, тобто
де
Запис (14) означає, що xs (r, q)є розв'язком задачі:
(13), (14) ‑ досить складна задача. Безпосередньо з вигляду (13), (14) можна сказати напевно лише одне: для знаходження параметрів страхування з боку страхової фірми потрібна "золота середина". Перший імпульс, який може виникнути у недосвідченого менеджера страхової компанії ‑ зменшити страхову винагороду r та збільшити страховий внесок q. На цьому шляху може виникнути небезпека позбутись клієнтів взагалі і збанкротувати внаслідок надмірної жадібності. Страховій компанії не може бути добре, якщо буде погано її клієнтам. Водночас завелика страхова винагорода та замалий страховий внесок можуть призвести також до банкрутства компанії, оскільки сумарна страхова винагорода може перевищити сумарний-страховий внесок.
Числовий приклад Розглянемо економічну постановку задачі. В нашому прикладі розглядається страхова компанія (страховик) та декілька осіб (страхувальників). Кожен із страхувальників займається певним видом господарської діяльності від якої він отримує певні прибутки чи несе певні затрати на цю діяльність. Тобто для кожного з них є заданими наступні величини: Н - дохід від господарської діяльності с - затрати на проведення господарської діяльності v - затрати на проведення попереджувальних заходів р - ймовірність настання страхового випадку Q - витрати при настанні страхового випадку
а для страховика є відомою:
значення яких приведено в таблиці
Оперуючи цими даними ми обчислюємо: • Величину страхового внеску для страхувальника (г) за формулою:
• Величину страхової виплати страховика (h) за формулою:
• Величину прибутку страхувальника (g) за формулою: g = H - c - v. Обчисливши ці проміжні дані ми переходимо до розрахунку корисності по кожному страховому контракту для страховика та для кожного із страхувальників. Величину корисності для страхувальників Ef за формулою:
Величину корисності для страховика (ЕФ) за формулою:
Величину корисності страхування для страхувальників при підписанні страхового контракту
В таблиці наведені результати проведених розрахунків.
Одержавши вище наведені результати ми можемо зробити висновок про те, який із контрактів є оптимальним для страховика та страхувальників. Ми обчислюємо величину k для кожного страхового контракту за формулою k = Так в нашому випадку оптимальним контрактом страхування є контракт під номером 3, тому що величина k для даного контракту дорівнює: k = 4,8 - 3 = 1,8. Одержане значення є мінімальним з поміж усіх інших. А «міра» взаємовигідності по даному страховому контракту становить:
Задачі 1. Визначити тарифну нетто-ставку при страхуванні від пожеж, якщо ймовірність страхового випадку q=0,013, кількість застрахованих об'єктів N=500, середнє значення ступеня знищення об'єкта Розв ' язок: Основна частина нетто-ставки
Очікуване середнє число страхових випадків за рік
Для відносної характеристики розсіювання використовується коефіцієнт варіації, який дорівнює відношенню середньоквадратичного відхилення до математичного очікування:
Тоді ризикова надбавка
Нетто-ставка
2. Існують такі дані по страховій компанії за чотири квартали звітного року, тис.грн:
У звітному році умови страхування були стабільні, величина навантаження у тарифній ставці – 25%. З ймовірністю 0,95 розрахуйте нетто-ставку і брутто-ставку. Розв ' язок: Знаходимо збитковість кожного кварталу із 100 грн страхової суми: I кв. 150/32000=0,47; II кв. 135/32890=0,41; III кв. 148/34400=0,43; IV кв. 142/35000=0,41;
Знаходимо середню збитковість: (0,47+0,41+0,43+0,41)/4=0,43. Знаходимо відхилення збитковості кожного кварталу від середньої збитковості: 0,47 ‑ 0,43=+0,04; 0,41 ‑ 0,43=‑0,02; 0,43 ‑ 0,43=0; 0,41 ‑ 0,43=‑0,02. Знаходимо ризикову надбавку з ймовірністю 0,95%:
Знаходимо нетто-ставку: 0,43+0,046=0,476. Знаходимо брутто-ставку:
СУТНІСТЬ, ОСОБЛИВОСТІ І ЗАВДАННЯ АКТУАРНИХ РОЗРАХУНКІВ
АКТУАРНІ РОЗРАХУНКИ (actuarial calculations) ‑ система математичних і статистичних методів розрахунку страхових тарифів. Методологія актуарних розрахунків ґрунтується на застосуванні теорії ймовірностей, демографічної статистики та довгострокових фінансових обчислень інвестиційного доходу страховика. Актуарні розрахунки дають змогу визначити частку кожного страхувальника у створенні страхового фонду АКТУАРІЙ (actuary) ‑ офіційно уповноважена особа, фахівець, яка з допомогою методів математичної статистики розраховує страхові тарифи. На актуарія покладається відповідальність за те, щоб страхові фонди були достатніми на той момент, коли компанії доведеться виконувати свої зобов'язання за виданими полісами За допомогою актуарних розрахунків визначаються собівартість і вартість послуги, що надається страховиком страхувальнику. У більш узагальненій формі актуарні розрахунки можна представити як систему математичних і статистичних закономірностей, що регламентують взаємини між страховиком і страхувальниками. Визначення витрат, необхідних на страхування даного об'єкта, ‑ один із найбільш складних і відповідальних моментів у діяльності страховика. Форма, у якій обчислені витрати на проведення даного страхування, називається страховою (актуарною) калькуляцією. Роль актуарної калькуляції може бути розглянута у різних аспектах: з одного боку, вона дозволяє визначити собівартість послуги, що надається страховиком, а з іншого ‑ через неї створюються умови для всебічного аналізу й розкриття причин економічних, фінансових та організаційних успіхів чи недоліків у діяльності страховика. Актуарна калькуляція дозволяє визначити страхові премії до договору. Величина пред'явлених до сплати страхових премій припускає вимір прийнятого страховиком ризику. До складу актуарної калькуляції входить також визначення суми чи частки суми витрат на проведення страхування з обслуговування договору страхування. У актуарних розрахунках варто передбачати деякі особливості, пов'язані з практикою страхової справи. Найбільш важливими з них є: - події, що піддаються оцінці, мають ймовірний характер. Це відбивається на розмірі пред'явлених до сплати страхових премій; - в окремі роки загальна закономірність явища виявляється через масу відособлених випадкових подій, наявність яких припускає значні коливання в страхових преміях, пред'явлених до сплати; - визначення собівартості послуги, що надається страховиком, здійснюється у відношенні до всієї страхової сукупності; - необхідне виділення спеціальних резервів, що знаходяться в розпорядженні страховика, визначення оптимальних розмірів цих резервів; - прогнозування сторнування договорів страхування, експертна оцінка їх величини; - дослідження норми позичкового відсотка і тенденцій його зміни у конкретному часовому інтервалі; - наявність повного чи часткового збитку, пов'язаного із страховим випадком, що визначає потребу виміру величини його розподілу в часі і просторі за допомогою спеціальних таблиць; - дотримання принципу еквівалентності, тобто встановлення адекватної рівноваги між платежами страхувальника, вираженими через страхову суму, і страховим забезпеченням, наданим страховою компанією, завдяки отриманим страховим преміям; - виділення групи ризику в межах даної страхової сукупності. Основними завданнями актуарних розрахунків є: - дослідження й групування ризиків у межах страхової сукупності, тобто виконання вимоги наукової класифікації ризиків з метою створення гомогенної підсукупності в межах загальної страхової сукупності; - визначення математичної ймовірності настання страхового випадку, а також частоти й ступеня тяжкості наслідків заподіяння збитку як в окремих ризикових групах, так і в цілому по страховій сукупності; - математичне обґрунтування необхідних витрат на проведення страхування страховиком і прогнозування тенденцій їх розвитку; - математичне обґрунтування необхідних резервних фондів страховика, пропозиції конкретних методів і джерел їх формування. Питання актуарних розрахунків займають центральне місце у діяльності будь-якої страхової компанії. Значення актуарних розрахунків обумовлюється тим, що страховик, як правило, проводить ряд різних за змістом і характером видів страхування, які вимагають адекватного математичного виміру узятих за договорами зобов'язань. При організації актуарних розрахунків необхідно передбачати деякі загальні питання, що не залежать від конкретного виду страхування. До них відносяться: - визначення нетто-премії; - визначення надбавки за ризик; - визначення витрат на проведення страхування. Незважаючи на методологічну єдність усіх актуарних розрахунків, практика їх проведення допускає різні варіації й варіанти, пов'язані із специфікою окремих видів, підвидів та галузей страхування. У цілому є визначена залежність конкретної практики актуарних розрахунків від даного виду страхування, обраної системи забезпечення і способу проведення страхування. За допомогою актуарних розрахунків визначається розмір страхових премій, пропонованих до сплати. Одиницею розрахунків служить окремий об'єкт, включений у страхову сукупність. При визначенні розміру страхових платежів одиниця розрахунків може розглядатися в різних ієрархічних рівностях: у цілому для країни, по окремих регіонах, з урахуванням особливостей даного конкретного району і неоднаковістю прояву ризику в часі і просторі. Інша особливість актуарних розрахунків по окремих видах страхування пов'язана з тією обставиною, що в майновій групі у зв'язку з великими коливаннями ризиків визначається спеціальна надбавка за ризик. Подібна надбавка звичайно не обчислюється при актуарних розрахунках по особовому страхуванню (хоча в принципі можлива), тому що обсяг страхової сукупності досить великий, а страхові суми порівняно невеликі. Вплив соціальних моментів діяльності людини при організації актуарних розрахунків також припустимий. Актуарні розрахунки проводяться в залежності від мети, що поставив страховик, і загальноекономічних умов даної країни. Це означає, що в залежності від деяких соціальних умов заключний актуарний розрахунок може мати декілька варіантів при наявності однакових об'єктивних факторів (прояв ризику, ступінь ймовірності, витрати на проведення страхування). Актуарні розрахунки класифікуються по видах страхування. Вони можуть бути також класифіковані за часом складання на планові й звітні (наступні). На практиці звичайно складаються наступні актуарні розрахунки за вже проведеними операціями страховика. Ці розрахунки орієнтовані на діяльність страховика у майбутньому при проведенні даного виду страхування. Планові актуарні розрахунки складаються тільки в тому випадку, коли передбачається введення нового виду страхування, по якому відсутні будь-які достовірні спостереження ризиків. Звичайно використовують результати актуарних розрахунків за однотипними чи близькими за змістом видами страхування, що вже проводяться компанією. Після закінчення 3-4 років планові актуарні розрахунки коригуються з урахуванням аналізу отриманих статистичних даних. Так планові актуарні розрахунки перетворюються в звітні (наступні). У залежності від ієрархічної рівності актуарні розрахунки можуть бути загальними (для всієї країни) і зональними (для окремого району). Структура страхової калькуляції, отриманої за результатами актуарних розрахунків, пов'язана із співвідношенням між окремими елементами витрат, включених у калькуляцію. Це дозволяє зробити порівняння як страхової калькуляції в цілому, так і її окремих елементів. З часом структура страхової калькуляції зазнає змін. Вона обумовлена змінами в розвитку ризику, новою страховою політикою, станом конкурентної боротьби на ринку і т. ін.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-22; просмотров: 123; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.198.13 (0.013 с.) |

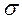 ) здійснюється у такому порядку:
) здійснюється у такому порядку: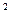 =0,000676;
=0,000676;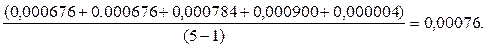
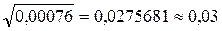 грн
грн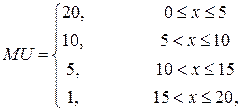 (?)
(?)
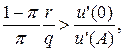 (2)
(2)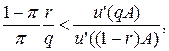 (3)
(3)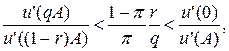 (4)
(4)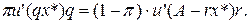 (5)
(5)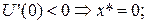 (2')
(2')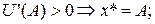 (3')
(3')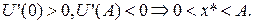 (4')
(4')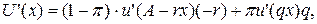
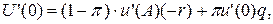
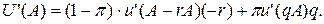
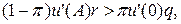

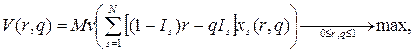 (13)
(13)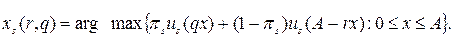 (14)
(14)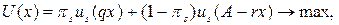
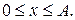
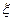 - відношення до ризику,
- відношення до ризику,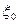 - величина надбавки до нетто-ставки.
- величина надбавки до нетто-ставки.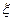
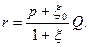
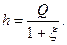
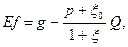
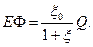
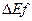 за формулою:
за формулою: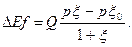
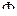
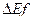
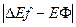 , і порівнюємо їх між собою. Тобто шукаємо мінімальне значення. Одержавши дану величину ми обчислюємо «міру» взаємовигідності даного страхового контракту для страховика і страхувальника.
, і порівнюємо їх між собою. Тобто шукаємо мінімальне значення. Одержавши дану величину ми обчислюємо «міру» взаємовигідності даного страхового контракту для страховика і страхувальника.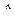 = 4,8 + З = 7,8.
= 4,8 + З = 7,8.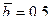 , середньоквадратичне відхилення від середнього значення
, середньоквадратичне відхилення від середнього значення 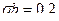 . Рівень гарантії безпеки y рівний 0,9.
. Рівень гарантії безпеки y рівний 0,9.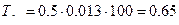
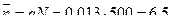
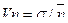 . Коефіцієнт варіації ступеня збитку
. Коефіцієнт варіації ступеня збитку