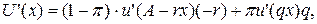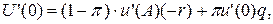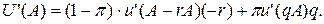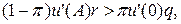Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гранична сподівана корисність та сподівання граничної корисності
Припустимо, обсяг страхування збільшився на одиницю. Тоді у разі страхового випадку відшкодування зросте на величину q, а корисність ‑ на величину MU (qx)∙ q, де MU ‑ гранична корисність залишку активу. Якщо страхового випадку не буде, то втрата клієнта збільшиться на величину r, а корисність ‑ на величину MU (A ‑ rx)∙ r. Останню величину можна інтерпретувати як граничну шкоду (або зі знаком мінус), як граничну корисність страхування за відсутності страхового випадку, а величину MU (qx)∙ q ‑ як граничну корисність страхування за наявності страховоговипадку. Сподівана гра нична корисність дорівнюватиме величині:
Водночас ця величина показує приріст сподіваної корисності внаслідок зміни (збільшення) обсягу страхування, тобто вона є й граничною сподіваною корисністю. Отже, гранична сподівана корисність страхування збігається із сподіваною граничною корисністю. Цей факт також негайно підтверджується відомими правилами диференціювання: Величина и'(А ‑rx)(- r) є іншим записом величини MU (A ‑ r х) ∙ (- r), тобто граничною корисністю страхування за відсутності страхового випадку, u '(qx) q ‑ величини MU (qx)∙ q, тобто граничною корисністю страхування за наявності страхового випадку. З припущення про монотонне зростання функції корисності випливає цікавий факт: гранична корисність страхування ‑ додатна величина у разі страхового випадку (коли трапляється нещастя) і від'ємна ‑ за відсутності страхового випадку. Наперший погляд, парадоксальне твердження, але за більш детального розгляду воно відповідає логіці поведінки індивіда: якщо все гаразд, то гроші, витрачені на страхування,здаються марно втраченими; коли ж трапляється біда, то кожна вкладена гривня в страхування дає незрівнянно більшу користь. Теорема про рівновагу Теорема 1 Припустимо, клієнт ‑ несхильний до ризику й має монотонно зростаючу та диференційовану функцію корисності. У цьому разі,
то клієнт ухиляється від страхування, якщо
то клієнт страхує весь актив; якщо ж
то клієнт страхує частку свого активу (але не весь актив), причому для обсягу страхування, який забезпечує максимальну сподівану корисність х*, виконується:
Доведення Оскільки клієнт несхильний до ризику, то його функція корисності увігнута. Доведення базується на властивостях увігнутих функцій. Дійсно, з властивостей увігнутих функцій з увігнутості функції корисності и(х) випливає увігнутість функції сподіваної корисності u (x). Звідси, гранична сподівана корисність U '(x) спадає у разі зростання обсягу страхування. Отже, максимальна гранична сподівана корисність буде спостерігатись у точці 0. За максимального обсягу страхування гранична сподівана корисність буде мінімальною. Таким чином, можна виписати співвідношення для задачі (1):
Оскільки, то
Сполучаючи останні три співвідношення з (2'), (3'), (4') отримуємо доведення теореми про рівновагу.
Аналіз рівноваги Рівняння (5) допускає таке читання: в стані рівноваги гранична корисність страхування за наявності страхового випадку, перемножена на його імовірність, збігається з граничною шкодою від страхування за відсутності страхового випадку, перемноженою на його імовірність. Отже, клієнт балансує граничну шкоду та граничну корисність для визначення найбільш привабливого для себе обсягу страхування, причому, враховуючи імовірність страхового випадку. Нерівність (2) можна переписати таким чином:
тобто, якщо гранична шкода першої одиниці страхування за відсутності страхового випадку, перемножена на імовірність недоторканості активу, перевищує граничну корисність останньої одиниці активу за умови, що страховий випадок трапився, перемножену на його імовірність, то клієнт не схильний до страхування в будь-яких обсягах. Аналогічну інтерпретацію можна дати й для нерівності (3), коли переписати її у вигляд
маючи на увазі, що величина u '((1- r) A) r характеризує граничну шкоду від страхування за максимально можливого його обсягу за умови недоторканості активу, a u '(qA) q ‑ граничну корисність максимально можливого обсягу страхування за умови, коли трапляється страховий випадок.
Звернемось ще раз до рівняння рівноваги (5), для того щоб помітити цікаву деталь: оскільки здебільшого імовірність недоторканості активу 1-πістотно більша імовірності страхового випадку π, то гранична корисність страхування за умови страхового випадку повинна бути набагато більшою від граничної шкоди від страхування за умови, коли страховий випадок не трапляється.
|
||||||
|
Последнее изменение этой страницы: 2020-11-22; просмотров: 81; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.45.162 (0.005 с.) |


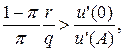 (2)
(2)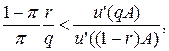 (3)
(3)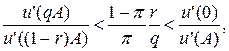 (4)
(4)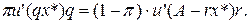 (5)
(5)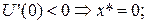 (2')
(2')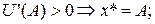 (3')
(3')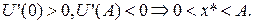 (4')
(4')