3) Погрешность обработки валов Dd подчиняется закону нормального распределения с  , мкм и
, мкм и 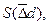 мкм. Известны: εS, εi, N. Определить процент брака (данные к задаче в таблице 2.10.).
мкм. Известны: εS, εi, N. Определить процент брака (данные к задаче в таблице 2.10.).
Таблица 2.10
| Вариант | 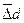 , мкм , мкм
| 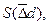 мкм мкм
| εS, мкм | εi,мкм | N, шт. |
| 1 | -80 | 32 | 0 | -190 | 400 |
| 2 | -95 | 33 | 0 | -180 | 500 |
| 3 | -110 | 39 | 0 | -200 | 300 |
| 4 | -120 | 39 | 0 | -200 | 500 |
| 5 | -80 | 43 | 0 | -160 | 500 |
| 6 | -120 | 40 | 0 | -200 | 400 |
| 7 | -110 | 45 | 0 | -200 | 500 |
| 8 | -90 | 39 | 0 | -150 | 200 |
| 9 | -65 | 25 | 0 | -190 | 500 |
| 10 | -75 | 30 | 0 | -190 | 500 |
| 11 | -85 | 32 | 0 | -200 | 200 |
| 12 | -90 | 33 | 0 | -150 | 400 |
| 13 | -75 | 39 | 0 | -140 | 300 |
| 14 | -90 | 40 | 0 | -160 | 300 |
| 15 | -110 | 41 | 0 | -180 | 400 |
| 16 | -90 | 39 | 0 | -160 | 200 |
| 17 | -125 | 41 | 0 | -200 | 500 |
| 18 | -70 | 40 | 0 | -140 | 300 |
| 19 | -60 | 39 | 0 | -150 | 200 |
| 20 | -90 | 42 | 0 | -170 | 400 |
| 21 | -75 | 30 | 0 | -120 | 200 |
| 22 | -70 | 32 | 0 | -110 | 500 |
| 23 | -80 | 33 | 0 | -130 | 300 |
| 24 | -80 | 34 | 0 | -120 | 200 |
| 25 | -60 | 35 | 0 | -105 | 400 |
4) Определить точность процесса обработки и возможный процент брака при тонком точении шейки вала диаметром D мм. Измерение деталей выборки N, шт. показали, что рассеивание размеров подчиняется нормальному закону распределения по данным выборки 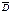 , мм и S, мм (
, мм и S, мм (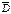 - средний размер деталей выборки; S – среднее квадратическое отклонение их размеров). Исходные данные к задаче в таблице 2.11.
- средний размер деталей выборки; S – среднее квадратическое отклонение их размеров). Исходные данные к задаче в таблице 2.11.
Таблица 2.11.
| Вариант | D, мм | N, шт. | 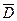 , мм , мм
| S, мм |
| 1 | 25-0,03 | 50 | 24,986 | 0,005 |
| 2 | 50-0,023 | 50 | 49,992 | 0,004 |
| 3 | 35-0,028 | 50 | 34,96 | 0,005 |
| 4 | 40-0,03 | 50 | 39,98 | 0,004 |
| 5 | 60-0,023 | 20 | 59,96 | 0,003 |
| 6 | 40-0,15 | 20 | 39,88 | 0,025 |
| 7 | 30-0,1 | 50 | 29,97 | 0,019 |
| 8 | 130+0,1 | 50 | 129,98 | 0,026 |
| 9 | 25-0,033 | 50 | 24,990 | 0,005 |
| 10 | 52+0,019 | 20 | 51,985 | 0,005 |
| 11 | 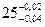
| 50 | 24,986 | 0,004 |
5) Погрешность обработки отверстий D d подчиняется закону нормального распределения с DС, мкм и S(D d), мкм. Известны: lS, li. Определить процент брака. Исходные данные к задаче в таблице 2.12.
Таблица 2.12
| Вариант | 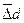 , мкм , мкм
| 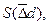 мкм мкм
| lS, мкм | li,мкм | N, шт. |
| 1 | 85 | 35 | 190 | 0 | 500 |
| 2 | 80 | 31 | 180 | 0 | 400 |
| 3 | 72 | 29 | 160 | 0 | 200 |
| 4 | 120 | 39 | 200 | 0 | 500 |
6) Определить точность обработки и возможный процент брака при тонком точении отверстия диаметром D, мм. Измерение деталей выборки из N шт. показали, что рассеивание размеров подчиняется нормальному закону распределения с параметрами по данным выборки  , мм и S, мм (
, мм и S, мм (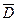 - средний размер деталей выборки; S – среднее квадратическое их размеров). Исходные данные к задаче в таблице 2.13
- средний размер деталей выборки; S – среднее квадратическое их размеров). Исходные данные к задаче в таблице 2.13
Таблица 2.13
| Вариант | D, мм | N, шт. |  , мм , мм
| S, мм |
| 1 | 25-0,03 | 50 | 25,014 | 0,005 |
| 2 | 50+0,023 | 50 | 50,008 | 0,004 |
| 3 | 35+0,028 | 50 | 35,01 | 0,005 |
| 4 | 40+0,032 | 50 | 40,018 | 0,004 |
Пример решения.
Определить число годных и бракованных деталей при обработке в партии N=200 шт. Среднеквадратическое отклонение по результатам измерения составляет S=0,019 мм. Заданный размер А=30-0,1мм. Смещение кривой распределения размеров относительно середины поля допуска не происходит.
Решение:
1) Пусть наше распределение соответствует закону нормального распределения
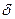 = p. S=1,25.0,019=0,02375 мм
= p. S=1,25.0,019=0,02375 мм
2) Зона фактического рассеивания размеров
D = 6 d = 6 ×0,02375=0,1425 мм
3) Сравниваем фактическое поле рассеивания с полем допуска
D >Т, т.е. 0,1425 >0,1 мм
так как фактическое поле рассеивания больше поля допуска, значит есть вероятность появления брака.
4) Половина поля допуска:
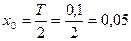 мм
мм
5) Определяем величину Z и функцию Лапласа:
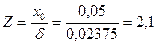
Затем по [2] приложения 1 находим значение функции Лапласа Ф(z) для данного значения Z.
Ф(z=2.1)=0,4820, т.е. 48,20%
Так как смещение кривой распределения размеров относительно середины поля допусков не происходит, то для всей партии
Ф(z)=48,20.2=96,40%
Значит годных деталей 96,40%, что соответствует 193 деталям партии, а бракованных -3,60%, что соответствует 7 деталям партии.
|
| Поделиться: |






