Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Натуральные, целые и рациональные числаСтр 1 из 18Следующая ⇒
Содержание
Числа Первичная обработка результатов эксперимента Явления, происходящие в природе и обществе, сложны и разнообразны. Ученые изучают разные стороны этих явлений, причем каждая наука вырабатывает свои методы исследования. Например, преступность изучают юристы, социологи, психологи, медики. Есть тут серьезная работа и для математиков. Их задача – подвергнуть математической обработке огромный статистический материал – отчеты органов внутренних дел и прочее – содержащий различные числовые данные. Цель этой работы – выделить наиболее существенные сведения об интересующем явлении. Результаты обработки представляются в виде таблиц, диаграмм, графиков и различных числовых характеристик, которые называются параметрами. Важнейшие из них – среднее арифметическое и дисперсия. Среднее арифметическое Понятие среднего значения используется для описания разнообразных явлений природы и общественной жизни: средняя температура воздуха, средняя зарплата, средняя продолжительность жизни. Например, для изучения общественного мнения проводят опрос не всех избирателей, а лишь небольшой части населения. По результатам прогнозируют популярность кандидатов у различных групп населения в разных регионах. При грамотной математической обработке результатов опроса выводы будут достаточно точно отражать реальную ситуацию. Средней величиной обычно называют среднее арифметическое. Пусть
Пример. Количество ДТП на улицах города в первую декаду декабря: 6 8 10 7 6 11 9 8 7 11. Среднее арифметическое этих чисел
показывает среднее число ДТП в день. В сводке за следующие 10 дней такие данные: 0 5 7 7 12 11 14 13 7 6. Их среднее арифметическое
Отсюда видно, что средние значения 8,3 и 8,2 отличаются друг от друга значительно меньше, чем число ДТП за каждый день. Поэтому среднее число ДТП можно прогнозировать, причем достаточно точно. Этот факт подтверждается и отчетами ГАИ за много лет. Из них также видно, что чем больше срок отчетности (декада, месяц, квартал, …), тем устойчивее средняя величина. Такое свойство средних значений представляет собой одно из важнейших проявлений закона больших чисел, открытого знаменитым русским математиком П.Л.Чебышевым. Если исходные данные содержат несколько десятков чисел, то составляют таблицу, в которой указывают для каждой величины, сколько раз она наблюдалась. Пример. Число правонарушений в городе, совершенных подростками за первые 20 дней сентября: 8 6 13 4 13 13 12 9 7 6 12 14 13 12 17 6 8 12 7 12. По этим данным составим таблицу:
Таблица 1
Здесь Среднее число правонарушений в день:
Отсюда формулу (1) можно переписать так:
Здесь
Таблицу 1 можно переписать так, чтобы во второй строке вместо числа дней стояла доля, которую это число составляет от числа всех дней, т.е. частота: Таблица 2.
Используя понятие частоты, подсчитаем среднее значение
Таким образом, среднее арифметическое равно сумме произведений чисел, взятых из первой строки таблицы 2, на их частоты. Преобразуем таким же способом формулу(2). Возьмем частоты:
Отсюда
Этой формулой можно пользоваться и в том случае, когда не известны величины Пример. В некотором городе каждому пассажиру междугородного автобуса вручают страховой полис на 50000 руб., взимая за это 50 руб. Какова средняя прибыль страховой компании от продажи одного полиса, если несчастные случаи происходят в среднем с одним пассажиром из 10000? Решение. Прибыль может принимать 2 значения: 50 руб., если несчастного случая не произошло, и – 49950 руб. при гибели пассажира. Составим таблицу частот:
Отсюда среднее значение прибыли:
Элементы комбинаторики Понятие вероятности Случайные события Все наблюдаемые при определенных условиях события можно разделить на три вида: достоверные, невозможные и случайные. Всякий раз, когда указанные условия выполняются, говорят, что происходит испытание. Например, стрелок стреляет по мишени, разделенной на 4 области. Выстрел – это испытание. Попадание в определенную область мишени – событие. Другой пример. В урне имеются цветные шары. Из урны наудачу берут один шар. Извлечение шара из урны есть испытание. Появление шара определенного цвета – событие. Достоверным называется такое событие, которое происходит при каждом испытании. Невозможным называется событие, которое не может произойти не при одном испытании. Случайным называется событие, которое в данном испытании может произойти, а может и не произойти. Событие «стрелок поразил одним выстрелом сразу 4 области» - невозможное. Событие «стрелок поразил одну из 4-х областей» - достоверное. Событие «стрелок поразил 1-ю область» - случайное. Случайные события обозначаются буквами А,В,С,…, достоверное событие – W(иногда U), невозможное – ø (иногда V) Суммой событий А и В называется такое событие А+В, которое состоится при появлении или события А, или события В, или обоих событий вместе. Произведением событий А и В называется событие АВ, которое происходит при одновременном наступлении обоих событий. Аналогично определяется сумма и произведение большего числа событий. Событие, которое состоится, если событие А произойдет, а событие В не произойдет, называется разностью событий А и В и обозначается А - В. Если при каждой реализации комплекса условий, когда происходит событие А, происходит и событие В, то говорят, что А влечет за собой В, и обозначают А Ì В или В Ì А. Если имеет место одновременно и А Ì В, и В Ì А, то события А и В называются равносильными (эквивалентными). В этом случае пишут А=В. События А и В называются несовместными, если их совместное наступление невозможно, т.е. А В = ø Например, при одном бросании монеты выпадает либо орел (событие А), либо решка (событие В). Событие А и В несовместны. Два несовместных события А и В называются противоположными, если при всякой реализации комплекса условий одно из них обязательно происходит. Иначе говоря, А и В будут противоположными событиями, если для них одновременно выполняются два соотношения АВ= ø, А + В= W. Пишут
Имеют место важные соотношения (законы де Моргана):
Пример. Событие А – взятая наудачу деталь – 1-го сорта, событие В – 2-го сорта, событие С – 3-го сорта. Что представляют собой следующие события: А + В;
Решение. А+В – событие, состоящее в том, что наступит хотя бы одно из событий А и В; следовательно, А+В – деталь 1-го или 2-го сорта. Так как А+С – деталь 1-го или 3-го сорта, то противоположны этому событие
Пример. Упростить выражение: Решение. Используем обычные алгебраические правила раскрытия скобок с учетом действий над событиями: Событие АА=А, событие Теперь запишем окончательное выражение: (А+В)(А+ Пример. Пусть А,В,С – три произвольных события. Найти выражение для событий, которые состоят в следующем: 1) Произошло одно и только одно событие; 2) Произошло два и только два события; 3) Произошло не более двух событий. Решение. 1)Данное событие состоит в том, что произошло какое – либо одно из событий А,В или С, и при этом два других события не произошли, т.е. либо событие А
2). По аналогии с предыдущим:
3). Данное событие противоположно событию, состоящему в том, что произошли все три события А, В и С, поскольку все остальные их комбинации подходят под заданное определение. Таким образом, имеем:
или по закону де Моргана:
т.е. хотя бы одно из событий А, В или С не произошло. ■ События А 1, А 2,..., А n называются единственно возможными, если в результате испытания приходит какое – либо одно и только одно из этих событий. Говорят также, что эти события образуют полную группу. Например, игральную кость бросают 1 раз. События А 1, А 2, …, А 6 состоят, соответственно в выпадении чисел 1, 2,..., 6. Эти события являются единственно возможными. Каждое испытание можно описать с помощью событий, которые являются несовместными и единственно возможными. Эти события называются исходами испытания, или элементарными событиями. Совокупность всех исходов испытания называется также пространством элементарных событий. События называются равновозможными, если есть основания считать, что ни одно из них не является более возможным, чем другое.
Например, появление герба или решки при бросании монеты – события равновозможные. Свойства вероятности Теорема 1. Если события А и В несовместны, то вероятность их суммы вычисляется по формуле Р(А+В) = Р(А) + Р(В) (1) Доказательство. Пусть число всех исходов равно n. В число исходов, благоприятных событию А+В, входят все исходы, благоприятные событию А, и все исходы, благоприятные событию В. Так как А и В несовместны, то среди перечисленных исходов нет одинаковых. Поэтому
Задача. В урне 8 белых, 5 синих и 2 красных шара. Какова вероятность того, что вынутый шар будет синего или красного цвета? Решение. Обозначим события: А – «вынут синий шар», В – «вынут красный шар».
А и В несовместны, поэтому по формуле (1) Теорема 2. Справедлива формула:
Доказательство. События А и
С другой стороны, событие Задача. Один лотерейный билет выигрывает с вероятностью 0,001. Какова вероятность того, что владелец билета ничего не выиграет? Решение. Обозначим события: А – «выигрыш», В – «не выигрыш». По формуле (2)
Замечание. Формулу (1) можно распространить на любое число событий. Методом математической индукции доказывается, что если события А1, А2, …, А n попарно несовместны, то вероятность их суммы вычисляется по формуле:
Функции и графики Степенные функции Уравнение квадратичной функции имеет вид: у = х2
Её график называется параболой. Точка О называется вершиной параболы.
Найдем обратную к ней функцию. Произведем замену  : :  . Отсюда . Отсюда  . Это две функции. Первая, . Это две функции. Первая,  , будет обратной для правой ветви параболы , будет обратной для правой ветви параболы  при при  . Вторая, . Вторая,  , будет обратной для левой ветви параболы , будет обратной для левой ветви параболы  при при  . .
Кубическая парабола имеет уравнение:
обратная к ней функция – уравнение
Графики этих функций также имеют симметрию относительно биссектрисы первого и третьего координатных углов.
Элементарные функции Кроме рассмотренных функций, в школе изучают тригонометрические функции – синус, косинус, тангенс, котангенс, секанс и косеканс. Главное свойство тригонометрических функций – периодичность, они все имеют период 2p, т.е.
Степенная, показательная и логарифмическая функции периодическими не являются. Самые разнообразные процессы в живой и неживой природе являются периодическими: колебательные и вращательные движения, волновые явления, движение планет, биоритмы и т.д. Функции, как и числа, можно складывать, вычитать, умножать и делить. При делении одной линейной функции на другую получим дробно – линейную функцию:
При сложении нескольких степенных функций получаются степенные многочлены:
Вейерштрасс доказал, что любую непрерывную функцию можно приближать многочленами с любой степенью точности. Например:
Чем больше n (число слагаемых), тем выше точность. Рассмотрим пример с массой кобальта. Ограничимся тремя слагаемыми:
Подставим в формулу (х = 0,676):
Это довольно грубо. Возьмем четыре слагаемых:
Более точное значение:
Если один многочлен поделить на другой, получится дробно - рациональная функция; например:
Над функциями можно производить операцию, которая не имеет аналога у чисел. Это операция композиции. Например, рассмотрим функции
Точно так же функция
представляет собой композицию функций Элементарными функциями называются постоянные, линейные, степенные показательные, логарифмические и тригонометрические функции, а также функции, которые получаются из них с помощью конечного числа арифметических операций и операций композиции. Корреляционная зависимость Рассмотрим пример. Между ростом и весом человека существует определенная зависимость. Однако много людей с одинаковым ростом имеют разный вес. Такая зависимость не является функциональной, поскольку для функций каждому х соответствует единственное значение у. Можно предположить, что вес зависит не только от роста, но и от размера талии и прочих параметров, но она является очень сложной и пока никем не обнаружена. Можно считать, что вес человека зависит от ряда случайных величин, среди которых рост является одной из основных. Эту зависимость описывают с помощью понятия вероятности. Зависимости такого рода называются стохастическими, вероятностными или статистическими. Важнейшим видом здесь является корреляционная зависимость. Рассмотрим в качестве примера вес и рост двадцати курсантов школы МВД:
Изобразим точки графически:
Точки лежат внутри некоторой области, или «облака». Заметно, что облако вытянуто вдоль какой – то наклонной прямой. Это означает, что Х и Y хорошо коррелированы, т.е. при увеличении роста вес, как правило, тоже увеличивается. Соединим точки отрезками, получим эмпирическую ломаную регрессии. При большем числе измерений эта ломаная больше похожа на прямую. Прямая, к которой стремится ломаная, называется регрессией. Она является наилучшим решением задачи построения прямой, относительно которой сумма квадратов вертикальных отклонений экспериментальных точек будет наименьшей. Это задача метода наименьших квадратов. Уравнение искомой прямой имеет вид:
где Здесь
Подставим в формулы, получим:
Получим уравнение прямой:
Это эмпирическое уравнение регрессии. Величина r, определяемая по формуле:
называется коэффициентом корреляции. Здесь Отсюда
Свойства коэффициента корреляции: 1. 2. Если величины Х и Y независимы, то коэффициент корреляции равен нулю. 3. Если Х и Y связаны линейной зависимостью,то r = 1 или r = - 1, и наоборот. При совместном изучении двух случайных величин Х и Y прежде всего находят величину коэффициента корреляции, и если он оказывается близким к единице, то имеет смысл описывать корреляционную связь. Идея предела Предел функции Начнем с рассмотрения понятия непрерывности функции. В качестве примера возьмем функцию y = f (x) = x 2. Значение функции в точке 2, т.е. f(2) = 22 =4. Рассмотрим на оси х бесконечную последовательность точек с координатами: х1 = 2 – 1 = 1; х2 = 2 – ½ = 3/2; х3 = 2 – ¼ = 1 ¾; … Любое из этих чисел меньше двух. Эти точки скапливаются около точки х0 = 2.
Разности х0 – х k, k >0 уменьшаются в 2 раза и могут стать меньше любого наперед заданного малого положительного числа. Поэтому говорят, что последовательность х1, х2, х3, … стремится к числу 2 или имеет своим пределом число2. при этом функция ведет себя так:
Это бесконечная последовательность. С увеличением k дроби стремятся к нулю, поэтому yk стремится к четырем:
lim – от латинского limes т.е. граница. Можно взять другую последовательность: 2 – 1; 2 – 1/10; 2 – 1/100 и т.д. Она также имеет своим пределом число 2. Таких последовательностей можно указать сколько угодно. Зависит ли предел функции от выбора последовательности, т.е. от того, каким образом переменная х стремится к двум? Нет, не зависит. Строгое определение предела функции включает в себя требование независимости от выбора последовательности. Когда предел функции в точке х0 равен значению функции в этой точке, говорят, что функция непрерывна в этой точке. Рассмотрим предел:
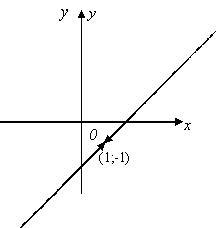
Здесь и числитель, и знаменатель при х = 1 обращаются в нуль. Поэтому нельзя найти предел, просто подставив единицу. Выполним преобразование:
Получили новую функцию g (x) = x – 2, где х может принимать любые значения. Во всех точках, кроме х = 1, выполняется тождество f (x) º g (x). График функции g (x) – это прямая. Функция f (x) в точке х = 1 не является непрерывной. График - тоже прямая, но без точки (1; - 1). Поэтому
1. Предел суммы нескольких функций равен сумме пределов этих функций. Например:
2. Предел произведения нескольких функций равен произведению пределов этих функций. Например:
Существуют два важных предела, которые называются замечательнымипределами: - первый замечательный предел: - второй замечательный предел: Производная Производная функции f (x) в точке х представляет собой следующий предел:
В числителе стоит приращение функции на отрезке [ x, x + h ]. Физический смысл производной: если рассмотреть функцию пути тела – s(t), то её производная представляет собой мгновенную скорость тела, т.е.
Производные от некоторых функций: 1. Производная от постоянной функции равна нулю, т.к., если функция не меняется, то её приращение равно нулю: f (x + h) – f (x) = 0/ 2. Производная степенной функции По определению
Вычтем х n, поделим почленно на h и запишем предел суммы как сумму пределов:
Все пределы, кроме первого, равны нулю, поэтому:
Правило применимо и для отрицательных степеней. 3. Производная синуса:
Аналогично доказывается, что 4. Производная от показательной функции у = ах:
При а = е получаем 5. Производная от логарифмической функции
При а = е получаем При вычислении производных пользуются следующими правилами, которые выводятся с помощью правил вычисления пределов:
Производная от сложной функции f (u (x)) вычисляется по формуле:
Например:
Приложения производной очень широкие. Производная от пути – это скорость. Производная скорости – ускорение, т.е. скорость изменения скорости. Задачи на нахождение наибольших и наименьших (экстремальных) значений заключаются в следующем: если непрерывная функция принимает в некоторой точке экстремальное значение и производная в этой точке существует, то производная в этой точке равна нулю. Пример. В тюрьме строят железную камеру для содержания особо опасных преступников. Какое наименьшее количество железа нужно для этой цели, если по санитарным нормам высота камеры не менее 2,5 м, а площадь – не менее 6 м2? Решение. Количество железа пропорционально площади поверхности камеры – параллелепипеда. Пол и потолок имеют площадь ab каждый, две боковые стены по 2,5 а, две другие стены – по 2,5 b. Тогда площадь равна S = 2 ab + 5 a + 5 b. При этом ab = 6 (b = 6/ a). Следовательно, S = 2×6 + 5(а + b) = 12 + (а + 6/ а). Величину а можно выбирать произвольно, она является переменной. Для минимизации функции S (a) следует приравнять нулю S ’ (a):
Отсюда Интеграл Различают определенный и неопределенный интеграл. Процедура нахождения производной по заданной функции называется дифференцированием, а обратная процедура, позволяющая находить по заданной производной исходную функцию, называется интегрированием. Результат интегрирования называется первообразнойфункцией. Поскольку производная от постоянной равна нулю, то
где С – любое действительное число. Поэтому, если для заданной функции f (x) существует одна первообразная F (x), то их существует бесконечно много: F (x) + C. Совокупность всех первообразных заданной функции f (x) называется неопределенныминтегралом и обозначается
Присутствующая всюду постоянная С называется постояннойинтегрирования. Простейшее применение определенного интеграла – вычисление площади под кривой. Чтобы найти S, разобьем отрезок [ a, b ] на маленькие отрезки длиной h. Верхняя граница заштрихованной фигуры находится между отрезками MN и PQ.
Такие неравенства запишем для каждого из отрезков длины h, на которые разбит отрезок [ a, b ], а затем все такие неравенства сложим. Получим неравенства:
S 1 и S 2 являются функциями от h. Если h неограниченно уменьшать Площадь получается как предел
где через F (x) обозначена первообразная функции f (x). Пример. Площадь под параболой
Математические структуры В основе математики лежит понятие множества. Множеством называют всякую совокупность каких-либо предметов. Предметы, из которых состоит множество, называются его элементами. Если элемент а принадлежит множеству М, то пишут Кольца и поля Числовые множества 1) 2) 3) 4) По этим же правилам производятся операции с многочленами, со всеми элементарными функциями, с рядами. В свойствах (1) отражены некоторые общие свойства указанных множеств. Любое множество с такими свойствами называется кольцом. Кольцо - это такое множество, на котором заданы две функции – сложение и умножение – которые должны подчиняться
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 82; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.86.155 (0.189 с.) |
 - некоторые числа. Их средним арифметическим называется число
- некоторые числа. Их средним арифметическим называется число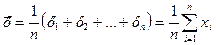 (1)
(1)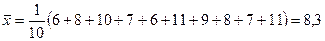


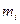
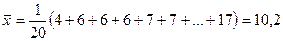 .
.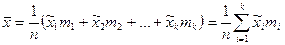 (2)
(2)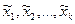 - различные среди заданных n чисел. При этом
- различные среди заданных n чисел. При этом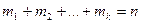 (3)
(3)
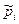
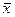 иным способом:
иным способом: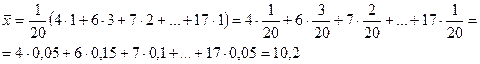
 ;
; 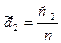 ;…;
;…; 
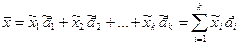 (4)
(4)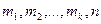 , но известны значения частот.
, но известны значения частот.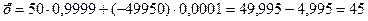 (руб.)
(руб.)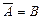 Очевидно,
Очевидно, 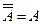
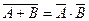
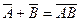
 ; А+С; АС; АВ+С?
; А+С; АС; АВ+С? – деталь 2-го сорта. АС – невозможное событие, поскольку деталь не может быть одновременно 1-го и 3-го сорта. АВ+С как сумма невозможного события и события с равно С, т.е. АВ+С – деталь 3-го сорта. ■
– деталь 2-го сорта. АС – невозможное событие, поскольку деталь не может быть одновременно 1-го и 3-го сорта. АВ+С как сумма невозможного события и события с равно С, т.е. АВ+С – деталь 3-го сорта. ■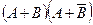
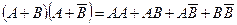
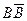 невозможное, поскольку не может одновременно произойти В и противоположное ему, т.е.
невозможное, поскольку не может одновременно произойти В и противоположное ему, т.е. 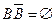 ; событие
; событие 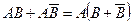 , т.е. в скобках имеет достоверное событие (произойдет или В, или не В), таким образом,
, т.е. в скобках имеет достоверное событие (произойдет или В, или не В), таким образом, 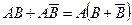 = А
= А 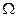 = А.
= А. )=А+А+ø, =А. ■
)=А+А+ø, =А. ■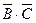 , либо событие
, либо событие 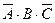 , либо событие
, либо событие 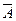
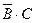 . Эти события несовместны, и их можно объединить в сумму:
. Эти события несовместны, и их можно объединить в сумму: ++
++ 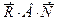 +
+ 
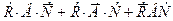
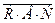 ,
, ,
,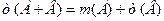 . Следовательно,
. Следовательно,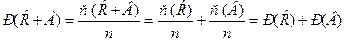 , что и требовалось доказать. ■
, что и требовалось доказать. ■
 .
.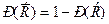 (2)
(2)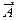 несовместны, поэтому по формуле (1)
несовместны, поэтому по формуле (1)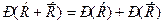
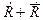 является достоверным, поэтому
является достоверным, поэтому 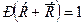 . Следовательно,
. Следовательно, 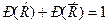 , что и требовалось доказать. ■
, что и требовалось доказать. ■ .
. (3)
(3)
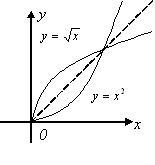

 ,
,

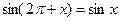 и т.д.
и т.д.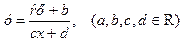
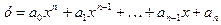
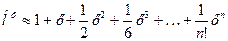
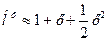
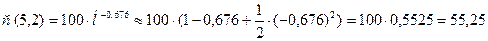 г.
г.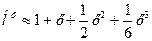
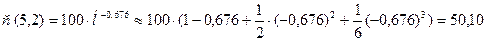 г.
г.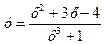
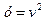 и
и 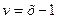 . Их композицией будет функция
. Их композицией будет функция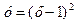 .
.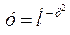
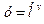 и
и 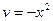 . Композиции двух или нескольких функций называются сложными функциями.
. Композиции двух или нескольких функций называются сложными функциями.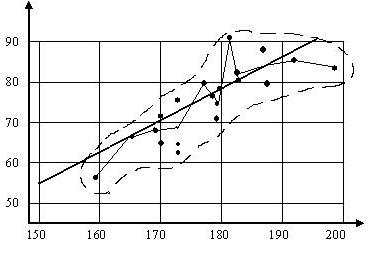
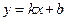 ,
,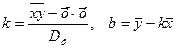 .
.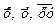 - средние значения роста, веса и их попарных произведений,
- средние значения роста, веса и их попарных произведений, 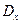 - дисперсия роста.
- дисперсия роста.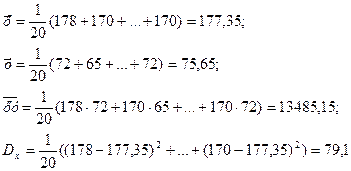
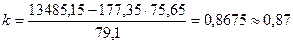
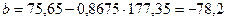
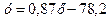
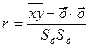 ,
,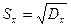 ,
, 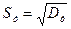 ,
, 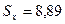 ,
, 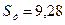 .
.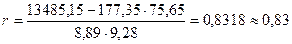 .
.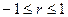 .
.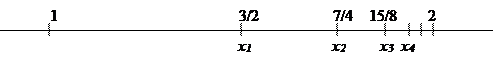
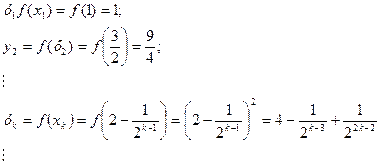
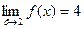 ,
,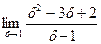
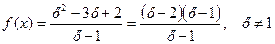
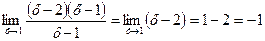
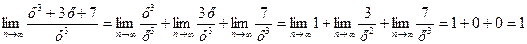
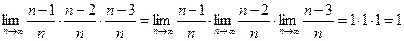
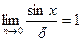 ;
;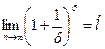
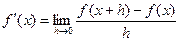
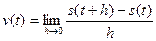
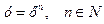 :
: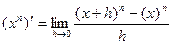 . По формуле бинома Ньютона:
. По формуле бинома Ньютона: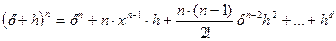 .
.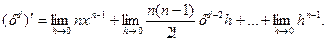
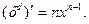
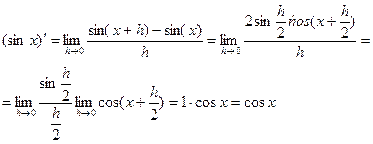
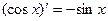 .
.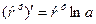
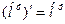 .
.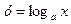 :
: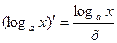
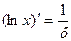 .
.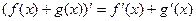 ,
,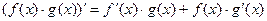
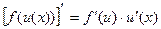
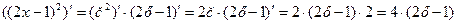 ;
;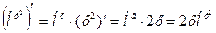
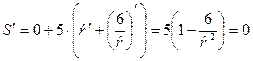
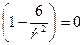 , следовательно,
, следовательно, 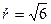 . При этом S будет наименьшей. Она равна
. При этом S будет наименьшей. Она равна 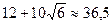 (м2).
(м2).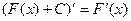 ,
,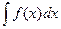 . Например:
. Например: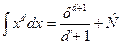 , т.к.
, т.к. 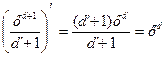 .
.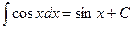 , т.к.
, т.к. 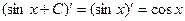 и т.д.
и т.д.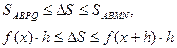
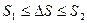

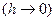 , то S 1 будет увеличиваться, а S 2 - уменьшаться. Обе суммы имеют своим общим пределом число S - площадь фигуры.
, то S 1 будет увеличиваться, а S 2 - уменьшаться. Обе суммы имеют своим общим пределом число S - площадь фигуры. или
или 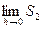 , который называется определенным интегралом и обозначается
, который называется определенным интегралом и обозначается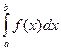 . Связь между определенным и неопределенным интегралами устанавливается формулой Ньютона – Лейбница:
. Связь между определенным и неопределенным интегралами устанавливается формулой Ньютона – Лейбница: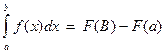 ,
,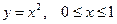 . Здесь а = 0, b = 1, поэтому
. Здесь а = 0, b = 1, поэтому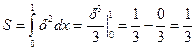 .
.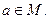 Например,
Например, 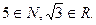 Если все элементы множества В принадлежат множеству А, то говорят, что множество В является подмножеством множества А, и записывают
Если все элементы множества В принадлежат множеству А, то говорят, что множество В является подмножеством множества А, и записывают 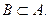 Множество, не содержащее ни одного элемента, называется пустым множеством и обозначается Ø. По определению считается, что пустое множество является подмножеством любого множества.
Множество, не содержащее ни одного элемента, называется пустым множеством и обозначается Ø. По определению считается, что пустое множество является подмножеством любого множества.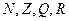 имеют одинаковые алгебраические свойства:
имеют одинаковые алгебраические свойства: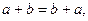 5)
5) 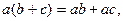
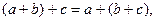 6)
6) 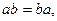 (1)
(1)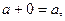 7)
7)