
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классическое определение вероятностиСодержание книги
Поиск на нашем сайте
Вероятность представляет собой количественную характеристику возможности наступления некоторого случайного события. Рассмотрим испытания, в результате которого может появиться событие А. Каждый исход, при котором осуществляется событие А, называется благоприятным событию А Например, событие А – «четное число очков при одном бросании игральной кости». Из шести равно возможных исходов (от 1 до 6) три исхода (2, 4, 6) являются благоприятными событию А. Вероятностью события А называется отношение числа исходов, благоприятных событию А, к числу всех исходов испытания. Обозначается вероятность события А через Р (А), т.е.
где m - число элементарных исходов, благоприятных А, n - число всех исходов. Здесь предполагается, что элементарные исходы несовместны, равновозможны и образуют полную группу. Из определения вероятности вытекают следующие ее свойства: 1) Вероятность достоверного события равна единице: Р (W) = 1. 2) Вероятность невозможного события равна нулю: Р (ø) = 0 3) Вероятность случайного события заключена между нулем и единицей, т.е. 0 ≤ P (A) < 1 При решении задач на вычисление вероятностей возникают трудности, связанные с определением числа тех или иных исходов испытания. В таких случаях используют комбинаторные формулы. Пример. Преступник знает, что шифр сейфа состоит из цифр 1, 3, 7, 9, но не знает, в каком порядке их набирать. Определить вероятность того, что первые 2 цифры шифра будут набраны верно, а также вероятность того, что сейф будет открыт с первой попытки. Решение. В первом случае исходом будет упорядоченная пара первых двух цифр шифра. Число таких пар равно числу размещений из 4 – х элементов по 2, Свойства вероятности Теорема 1. Если события А и В несовместны, то вероятность их суммы вычисляется по формуле Р(А+В) = Р(А) + Р(В) (1) Доказательство. Пусть число всех исходов равно n. В число исходов, благоприятных событию А+В, входят все исходы, благоприятные событию А, и все исходы, благоприятные событию В. Так как А и В несовместны, то среди перечисленных исходов нет одинаковых. Поэтому
Задача. В урне 8 белых, 5 синих и 2 красных шара. Какова вероятность того, что вынутый шар будет синего или красного цвета? Решение. Обозначим события: А – «вынут синий шар», В – «вынут красный шар».
А и В несовместны, поэтому по формуле (1) Теорема 2. Справедлива формула:
Доказательство. События А и
С другой стороны, событие Задача. Один лотерейный билет выигрывает с вероятностью 0,001. Какова вероятность того, что владелец билета ничего не выиграет? Решение. Обозначим события: А – «выигрыш», В – «не выигрыш». По формуле (2)
Замечание. Формулу (1) можно распространить на любое число событий. Методом математической индукции доказывается, что если события А1, А2, …, А n попарно несовместны, то вероятность их суммы вычисляется по формуле:
|
||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 248; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.28.79 (0.009 с.) |

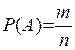 ,
,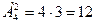 . Только один исход является благоприятным, и его вероятность равна 1/12. Во втором случае исходом является перестановка из цифр 1, 3, 7, 9. Число всех исходов
. Только один исход является благоприятным, и его вероятность равна 1/12. Во втором случае исходом является перестановка из цифр 1, 3, 7, 9. Число всех исходов  . Только один исход является благоприятным, поэтому вероятность открыть сейф с первой попытки равна 1/24.
. Только один исход является благоприятным, поэтому вероятность открыть сейф с первой попытки равна 1/24.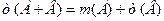 . Следовательно,
. Следовательно,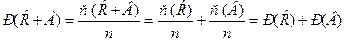 , что и требовалось доказать. ■
, что и требовалось доказать. ■
 .
.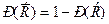 (2)
(2)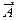 несовместны, поэтому по формуле (1)
несовместны, поэтому по формуле (1)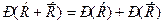
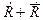 является достоверным, поэтому
является достоверным, поэтому 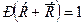 . Следовательно,
. Следовательно, 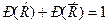 , что и требовалось доказать. ■
, что и требовалось доказать. ■ .
. (3)
(3)


