
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Перестановки, размещения, , сочетанияСодержание книги
Поиск на нашем сайте
В комбинаторных задачах комбинации предметов могут отличаться одна от другой числом предметов, их составом и порядком. Пример. В отделении 5 новобранцев: Белкин, Пенкин, Фенькин, Свечкин и Овечкин. Их учат рассчитываться по порядку. Каждый раз их перестраивают по – новому и расчет повторяется. Сколько раз сержант может повторить это упражнение разными способами? Можно обозначить солдат первыми буквами их фамилий. Например, ПСОФБ означает порядок, в котором солдаты расположились на построении. Все комбинации отличаются порядком букв и называются перестановками. Пусть дано множество из n элементов. Занумеруем их от 1 до n. Перестановкой из n элементов называется всякий способ нумерации этих элементов. Теорема 2. Число всех различных перестановок из n элементов равно n! Доказательство. Всякую перестановку из n элементов можно получить с помощью n действий: первое действие – выбор первого элемента, второе действие – выбор второго элемента и т.д., n – е действие – выбор элемента с номером n. Первый элемент можно выбрать n различными способами; второй выбирается из оставшихся n – 1 элементов, поэтому число всех способов выполнения второго действия будет n – 1. Далее останется n – 2 элемента, их можно разместить n – 2 способами. И т.д. Последнее действие можно выполнить одним способом. По правилу умножения число всех способов выполнения действий, т.е. число перестановок, равно Число перестановок обозначается Р n:
В случае с новобранцами (n = 5) Р n = 5! = 120. Пример. Свидетель происшествия запомнил, что четырехзначный номер автомобиля, скрывшегося с места происшествия, начинается с цифры 1, а завершается на 4, причем все цифры разные. Сколько автомобилей должна проверить автоинспекция? Решение. Вторую и третью цифры надо выбирать из восьми, а именно из 0, 2, 3, 5, 6, 7, 8, 9. Если выбрать вторую цифру восемью способами, то для третьей цифры останется 7 вариантов. Отсюда 8×7 = 56 способов. Нужно перебрать из восьми цифр по две с учетом их порядка, поскольку 1674 и 1764 – разные номера. Такие комбинации называют размещениями.
Размещением из n элементов по k называется всякая перестановка из k элементов, выбранных каким – либо способом из данных n элементов. Число размещений обозначается Теорема 3. Число всех размещений из n элементов по k вычисляется по формуле:
(в этой формуле k сомножителей). Доказательство. Аналогично теореме 2. Каждое размещение можно получить с помощью k действий. Первое действие можно выполнить n способами, второе – n - 1 способами и т.д., k действие – (n – k + 1) способами. По правилу умножения Для рассмотренного выше примера Пример. Из 10 депутатов поселкового совета 7 проголосовали «за». Каково число всех возможных вариантов голосования? Здесь порядок выбора не играет роли, поэтому комбинации отличаются только составом лиц. Такие комбинации называются сочетаниями. Сочетанием из n элементов по k называется всякая совокупность k элементов, выбранных каким – либо способом из данных n элементов. Теорема 4. Число всех сочетаний из n элементов по k вычисляется по формуле:
Доказательство. Возьмем какое – нибудь сочетание из n элементов по k: (a, b, c, …, f) - здесь k букв. Переставляя эти элементы всевозможными способами, получим k! всех размещений из n элементов по k одного и того же состава. Таким образом, из одного сочетания получается k! размещений. Следовательно, из
В последнем примере = 10, = 7, Другая формула для числа сочетаний имеет вид:
Теорема 5. Свойство
Доказательство. Если из n элементов выбрать k элементов, то останется (n – k) элементов. Следовательно, каждому сочетанию из n элементов по k соответствует определенное сочетание из n элементов по (n – k). Поэтому число тех и других сочетаний одинаково, что и требовалось доказать. ■ Формула (7) сокращает вычисления, например:
По определению 0! = 1, Числа
Эту формулу можно доказать методом математической индукции. Понятие вероятности Случайные события Все наблюдаемые при определенных условиях события можно разделить на три вида: достоверные, невозможные и случайные. Всякий раз, когда указанные условия выполняются, говорят, что происходит испытание. Например, стрелок стреляет по мишени, разделенной на 4 области. Выстрел – это испытание. Попадание в определенную область мишени – событие. Другой пример. В урне имеются цветные шары. Из урны наудачу берут один шар. Извлечение шара из урны есть испытание. Появление шара определенного цвета – событие. Достоверным называется такое событие, которое происходит при каждом испытании. Невозможным называется событие, которое не может произойти не при одном испытании. Случайным называется событие, которое в данном испытании может произойти, а может и не произойти. Событие «стрелок поразил одним выстрелом сразу 4 области» - невозможное. Событие «стрелок поразил одну из 4-х областей» - достоверное. Событие «стрелок поразил 1-ю область» - случайное. Случайные события обозначаются буквами А,В,С,…, достоверное событие – W(иногда U), невозможное – ø (иногда V) Суммой событий А и В называется такое событие А+В, которое состоится при появлении или события А, или события В, или обоих событий вместе. Произведением событий А и В называется событие АВ, которое происходит при одновременном наступлении обоих событий. Аналогично определяется сумма и произведение большего числа событий. Событие, которое состоится, если событие А произойдет, а событие В не произойдет, называется разностью событий А и В и обозначается А - В. Если при каждой реализации комплекса условий, когда происходит событие А, происходит и событие В, то говорят, что А влечет за собой В, и обозначают А Ì В или В Ì А. Если имеет место одновременно и А Ì В, и В Ì А, то события А и В называются равносильными (эквивалентными). В этом случае пишут А=В. События А и В называются несовместными, если их совместное наступление невозможно, т.е. А В = ø Например, при одном бросании монеты выпадает либо орел (событие А), либо решка (событие В). Событие А и В несовместны. Два несовместных события А и В называются противоположными, если при всякой реализации комплекса условий одно из них обязательно происходит. Иначе говоря, А и В будут противоположными событиями, если для них одновременно выполняются два соотношения АВ= ø, А + В= W. Пишут
Имеют место важные соотношения (законы де Моргана):
Пример. Событие А – взятая наудачу деталь – 1-го сорта, событие В – 2-го сорта, событие С – 3-го сорта. Что представляют собой следующие события: А + В; Решение. А+В – событие, состоящее в том, что наступит хотя бы одно из событий А и В; следовательно, А+В – деталь 1-го или 2-го сорта. Так как А+С – деталь 1-го или 3-го сорта, то противоположны этому событие
Пример. Упростить выражение: Решение. Используем обычные алгебраические правила раскрытия скобок с учетом действий над событиями:
Событие АА=А, событие Теперь запишем окончательное выражение: (А+В)(А+ Пример. Пусть А,В,С – три произвольных события. Найти выражение для событий, которые состоят в следующем: 1) Произошло одно и только одно событие; 2) Произошло два и только два события; 3) Произошло не более двух событий. Решение. 1)Данное событие состоит в том, что произошло какое – либо одно из событий А,В или С, и при этом два других события не произошли, т.е. либо событие А
2). По аналогии с предыдущим:
3). Данное событие противоположно событию, состоящему в том, что произошли все три события А, В и С, поскольку все остальные их комбинации подходят под заданное определение. Таким образом, имеем:
или по закону де Моргана:
т.е. хотя бы одно из событий А, В или С не произошло. ■ События А 1, А 2,..., А n называются единственно возможными, если в результате испытания приходит какое – либо одно и только одно из этих событий. Говорят также, что эти события образуют полную группу. Например, игральную кость бросают 1 раз. События А 1, А 2, …, А 6 состоят, соответственно в выпадении чисел 1, 2,..., 6. Эти события являются единственно возможными. Каждое испытание можно описать с помощью событий, которые являются несовместными и единственно возможными. Эти события называются исходами испытания, или элементарными событиями. Совокупность всех исходов испытания называется также пространством элементарных событий. События называются равновозможными, если есть основания считать, что ни одно из них не является более возможным, чем другое. Например, появление герба или решки при бросании монеты – события равновозможные.
|
|||||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 92; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.73.107 (0.012 с.) |

 (так обозначается функция факториал, т.е. произведение всех членов натурального ряда до n включительно). ■
(так обозначается функция факториал, т.е. произведение всех членов натурального ряда до n включительно). ■ (4)
(4) .
.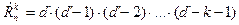 (5)
(5) , что и требовалось доказать. ■
, что и требовалось доказать. ■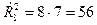 .
.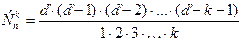 (6)
(6)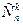 сочетаний получится
сочетаний получится  размещений, т.е.
размещений, т.е.  . Отсюда
. Отсюда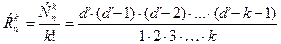 , что и требовалось доказать. ■
, что и требовалось доказать. ■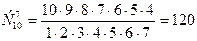
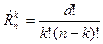
 :
: (7)
(7)
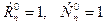 .
.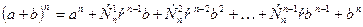
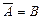 Очевидно,
Очевидно, 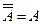
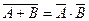
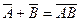
 ; А+С; АС; АВ+С?
; А+С; АС; АВ+С? – деталь 2-го сорта. АС – невозможное событие, поскольку деталь не может быть одновременно 1-го и 3-го сорта. АВ+С как сумма невозможного события и события с равно С, т.е. АВ+С – деталь 3-го сорта. ■
– деталь 2-го сорта. АС – невозможное событие, поскольку деталь не может быть одновременно 1-го и 3-го сорта. АВ+С как сумма невозможного события и события с равно С, т.е. АВ+С – деталь 3-го сорта. ■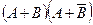
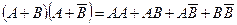
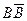 невозможное, поскольку не может одновременно произойти В и противоположное ему, т.е.
невозможное, поскольку не может одновременно произойти В и противоположное ему, т.е. 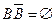 ; событие
; событие 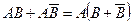 , т.е. в скобках имеет достоверное событие (произойдет или В, или не В), таким образом,
, т.е. в скобках имеет достоверное событие (произойдет или В, или не В), таким образом, 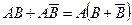 = А
= А 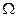 = А.
= А. )=А+А+ø, =А. ■
)=А+А+ø, =А. ■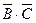 , либо событие
, либо событие 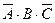 , либо событие
, либо событие 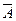
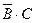 . Эти события несовместны, и их можно объединить в сумму:
. Эти события несовместны, и их можно объединить в сумму: ++
++ 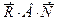 +
+ 
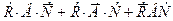
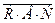 ,
, ,
,


