
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Десятичные дроби и действительные числаСодержание книги
Поиск на нашем сайте Дроби, у которых знаменатель представляет собой степень десяти, называются десятичными дробями. Записываются они особым образом:
Попытка записать любую обыкновенную дробь в виде десятичной иногда приводит к бесконечной десятичной дроби. Например, разделив «уголком», получим:
В этом случае бесконечная последовательность цифр содержит период – один и тот же повторяющийся набор цифр. Такие дроби называются бесконечными периодическими десятичными дробями. Можно доказать, что любая обыкновенная дробь записывается в виде бесконечной периодической десятичной дроби. Обратное также верно: любая бесконечная периодическая десятичная дробь представляет собой десятичную запись некоторой обыкновенной дроби. Рассмотрим на примере, как найти последнюю. Превратим в обыкновенные дроби числа q = 0,777… и р = 0,999… Умножим на 10, получим: 1) 10 q = 7,777(7), откуда 10 q = 7 + q; т.е. 9 q = 7, или 2) 10 р = 9,999(9), откуда 10 р = 9 + р, т.е. 9 р = 9, или р = 1. Замечание. Число 1 можно записать в виде 1,000…, т.е. с периодом 0; аналогично 0,24 = 0,24000… и т.д. Имеют ли смысл бесконечные непериодические десятичные дроби? Рассмотрим равнобедренный прямоугольный треугольник, длина катетов которого равна 1. Обозначим длину гипотенузы х. По теореме Пифагора х 2 = 12 + 12 = 2 (1) Докажем, что корни этого уравнения не являются рациональными числами. Предположим противное, что корнем (1) является дробь а 2 = 2× b 2 (2) Т.к. в правую часть (2) входит множитель 2, то а 2 – число четное, следовательно, число а – также четное, его можно записать в виде а = 2× с. Подставим это выражение в (2), получим (2× с)2 = 2× b 2, или, сократив на 2, 2× с 2 = b 2. Отсюда следует, что число b 2 также четное, следовательно, b – тоже четно. Поскольку а и b четные, дробь Найдем приближенные значения числа
Описанным способом можно находить десятичные приближения любого числа. Для обыкновенных дробей это просто деление уголком. Поскольку Всякую бесконечную десятичную дробь можно записать в виде суммы бесконечного числа слагаемых:
Такие суммы называются рядами. Первый ряд – так называемая геометрическая прогрессия, второй ряд прогрессией не является. Другой источник бесконечных непериодических десятичных дробей - корни квадратных, кубических и биквадратных уравнений. Например, уравнение х3=5 имеет корень
является, вообще говоря, бесконечной непериодической десятичной дробью. Рассмотрим два очень важных числа, которые являются бесконечными непериодическими дробями: число p и число е. Число p - отношение длины l произвольной окружности к её диаметру d:
Это число известно с глубокой древности. Вавилонские, египетские, китайские и греческие математики нашли различные приближенные значения p: 3; Архимед рассматривал вписанные в окружность правильные 2 n - угольники. Он нашёл, что Лейбниц доказал, что p можно представить в виде ряда:
(дроби в правой части не являются десятичными). Этот ряд позволяет находить приближенные значения p. Перепишем (4) так:
В скобках стоят положительные числа. Отбросив их, мы увеличиваем правую часть:
Отсюда С другой стороны, из равенства (4) получаем:
В скобках стоят положительные слагаемые. Отбрасываем их, получаем (правая часть уменьшается):
Это довольно грубая оценка p. Её можно улучшить, если взять больше слагаемых ряда (4). p=3,141592653589793… Неперово число е также может быть представлено в виде ряда:
где n! = 1×2×3×…× n, или «n факториал». Чтобы найти приближенное значение е, нужно в сумме (5) оставить несколько слагаемых, а остальными пренебречь. Чем больше слагаемых оставим, тем точнее результат: е = 2,718281828459045… С помощью ЭВМ можно подсчитать числа p и е с любой точностью. Числа p и е относятся к так называемым трансцендентным числам. Так называются числа, которые не могут быть корнями никакого уравнения вида (3) с целыми коэффициентами. Действительными или вещественными числами называются все бесконечные десятичные дроби. Множество таких чисел обозначается R. Оно включает в себя множество Q всех рациональных чисел, поэтому можно записать N Ì Z Ì Q Ì R Действительные числа, не являющиеся рациональными, называются иррациональными. Множество R является упорядоченным, т.е. любые два действительных числа можно сравнить между собой, указать, какое из них больше. Для этого нужно последовательно сравнивать цифры, стоящие на одинаковых позициях. Например, 2,381615 > 2,381529 На первых четырех позициях соответствующие цифры одинаковы, а 6>5. Единственное исключение из этого правила – не рассматривать периодические дроби с периодом 9. всякую такую дробь можно заменить равной ей конечной десятичной дробью, например: 0,999…=1; 0,42999…=0,43; 2,65999…=2,66. Свойства операций сложения и умножения действительных чисел: 1) a + b = b + a - переместительный закон (коммутативность); 2) (a + b)+ c = a +(b + c) – ассоциативность (переместительность) сложения; 3) (a × b) c = a × (b × c) – ассоциативность умножения; 4) a × (b + c)= a × b + a × c – дистрибутивность. Правило округления десятичных дробей, например, до сотых: 0,811»0,81; 0,812»0,81;…; 0,815»0,82; 0,816»0,82;…; 0,819»0,82. Действия со степенями: по определению: а 0 = 1, а n = a × a × a ×…× a (n сомножителей); Отсюда следует, что для любых m, n ÎN a m a n= a m+n: (a n)m= a nm: a n b n=(a × b)n. Число, которое при возведении в степень n даёт а, называется корнем степени n из а. Если число n нечетное, то существует только один действительный корень степени n из числа а; его обозначают Степень с дробным показателем определяется так:
Имеют смысл и выражения вида ах, где х – любое действительное число, например, Стандартная форма записи чисел реализуется в виде произведения двух множителей, первый из которых – между 1 и 10, а второй является степенью десяти, например 243507 = 2,43507×105; 0,184 = 1,84×10-1 и т.д. Такая форма используется при вычислениях с калькулятором, особенно если не хватает разрядов для точных вычислений. Она также используется в компьютерах.
|
||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 181; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |


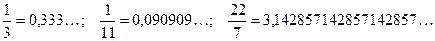
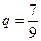 .
.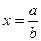 (a, b – целые числа). Если дробь
(a, b – целые числа). Если дробь 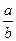 можно сократить, сделаем это, и далее будем считать, что дробь
можно сократить, сделаем это, и далее будем считать, что дробь 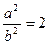 , или
, или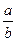 является сократимой. Это противоречит предположению о несократимости дроби
является сократимой. Это противоречит предположению о несократимости дроби 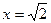 . Ясно, что 1< x <2. Далее, 1,42< x <1,52, поскольку 1,42 = 1,96<2, 1,52 = 2,25>2. С точностью до 0,1 х»1,4. Аналогично 1,41< x <1,42, т.к. 1,412<2, 1,422>2. С точностью до 0,01 имеем х»1,41. Аналогично 1,414< x <1,415, т.е. х»1,414 и т.д. Эта процедура позволяет находить все более точные приближения числа
. Ясно, что 1< x <2. Далее, 1,42< x <1,52, поскольку 1,42 = 1,96<2, 1,52 = 2,25>2. С точностью до 0,1 х»1,4. Аналогично 1,41< x <1,42, т.к. 1,412<2, 1,422>2. С точностью до 0,01 имеем х»1,41. Аналогично 1,414< x <1,415, т.е. х»1,414 и т.д. Эта процедура позволяет находить все более точные приближения числа 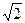 . Ни одно из них не может быть равно
. Ни одно из них не может быть равно 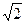 , т.к. все приближенные значения являются рациональными числами, а
, т.к. все приближенные значения являются рациональными числами, а 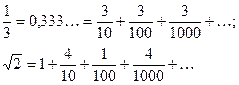
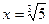 , уравнение 2х2=3 – корни
, уравнение 2х2=3 – корни 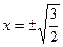 . Корень любого алгебраического уравнения с целыми коэффициентами
. Корень любого алгебраического уравнения с целыми коэффициентами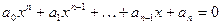 (3)
(3)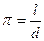
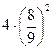 ;
; 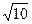 ;
; 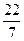 ;
; 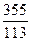 ;
; 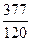 и др.
и др.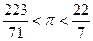 .
. (4)
(4)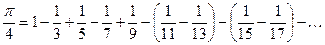
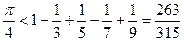
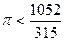 (оценка сверху).
(оценка сверху).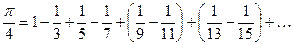
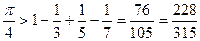
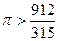 (оценка снизу), следовательно,
(оценка снизу), следовательно, 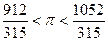 .
.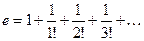 , (5)
, (5)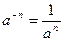 .
.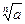 , или
, или 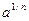 . Если n четное, а число а – положительное, то действительных корней будет два. Например,
. Если n четное, а число а – положительное, то действительных корней будет два. Например, 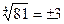 . Положительный корень называется арифметическим, и именно он обозначается
. Положительный корень называется арифметическим, и именно он обозначается 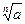 или
или 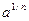 .
.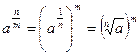
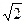 . Действия с такими степенями производятся по тем же правилам, что и с натуральными степенями, например,
. Действия с такими степенями производятся по тем же правилам, что и с натуральными степенями, например, 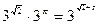 .
.


