Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема 1 (о градусной мере угла между двумя пересекающимися хордами). угол между двумя пересекающимися хордами имеет градусную меру, равную полусумме градусных мер тех дуг, на которые опирается⇐ ПредыдущаяСтр 15 из 15
Этот угол и угол, вертикальный к нему. Доказать: Доказательство: Способ 1. Рассмотрим D CEB.
Способ 2. Построим AG II CD.
Заметим, что È DG = È AC – симметричны относительно центра окружности.
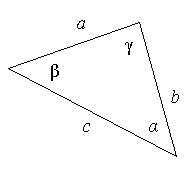
Доказать: Доказательство: Способ 1. Рассмотрим D CMB.
Способ 2. Проведем BE II MC.
Заметим, что È AB = È CE – симметричны относительно центра окружности. 6. 7. Задача по теме «Метод координат». Билет № 22 4. Теорема косинусов. Следствие из теоремы. Теорема: Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними. Дано: Треугольник АВС.
1 2. 3. Доказательство: Возможны три случая: 1) Угол С-острый; 2) угол С- тупой; 3) угол С –прямой. Докажем первое равенство, два других доказываются аналогично.
Второй способ решения задачи. Координатный метод.
Вывод: Теорема Пифагора является частным случаем теоремы косинусов. Рассмотрим следствия из теоремы косинусов.
| ||||||||||||||||||||||||||||||||||
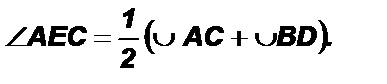



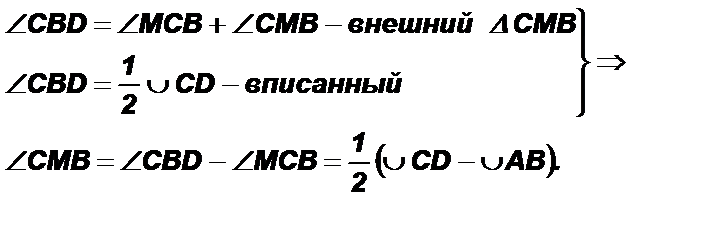

 Доказать:
Доказать: .;
.;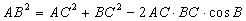 ;
; .
.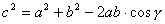 ;
; ;
;


 ABC
ABC A – острый, то cosA > 0,
б)
A – острый, то cosA > 0,
б)