
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Составим таблицу известных углов и значений синуса, косинуса и тангенса для них.
Дано:
Решение: СВ=x cos30 tg30 sin60 Дано:
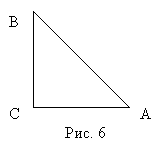
Решение: АС = СВ = x; АВ sin45 Задача по теме «Пропорциональные отрезки в круге». Билет № 7 Геометрическое место точек. Теорема о геометрическом месте точек, равноудаленных от двух данных точек, в геометрической и аналитической формах. Пусть геометрическая фигура имеет характерное свойство, определяющее, какие точки принадлежат фигуре. Тогда про эту фигуру говорят, что она является множеством точек, обладающих данным свойством (или геометрическим местом точек, обладающих данным свойством). Определение 1. Геометрическим местом точек называется фигура, которая состоит из всех точек плоскости, обладающих определенным свойством. Примеры: Окружность – это геометрическое место точек, равноудаленных от данной точки. Биссектриса угла – это геометрическое место точек, равноудаленных от сторон угла. 3) Серединный перпендикуляр к отрезку – это геометрическое место точек, равноудаленных от концов отрезка. Сущность метода геометрических мест точек, используемого при решении задач на построение, заключается в следующем. Пусть, решая задачу на построение, необходимо найти точку А, удовлетворяющую двум условиям. Геометрическое место точек, удовлетворяющих первому условию, есть некоторая фигура F 1, а геометрическое место точек, удовлетворяющих второму условию, есть некоторая фигура F 2. Искомая точка, удовлетворяет обоим условиям, т. е. принадлежит обеим фигурам, а значит, является точкой их пересечения. Алгоритм решения задачи на построение методом ГМТ. Выделить геометрические места точек, которым принадлежит данная точка. Построить выделенные геометрические места точек. Определить точки пересечения построенных ГМТ. Доказать, что именно эти точки пересечения соответствуют условиям задачи. Характерное свойство биссектрисы угла (прямая теорема). Каждая точка биссектрисы угла равноудалена от его сторон.
Пусть дан угол со сторонами m и n и вершиной А, где b – биссектриса угла. Возьмем произвольную точку D на биссектрисе b и опустим из нее перпендикуляры на стороны m и n. Рассмотрим полученные треугольники ABD и ACD.
Ð ABD = Ð ACD = 90°; Ð BAD = Ð CAD (b – биссектриса); AD – общая; D ABD = D ACD (как прямоугольные по гипотенузе и острому углу). Þ BD = CD. Характерное свойство биссектрисы угла (обратная теорема). Точка угла, равноудаленная от его сторон, лежит на биссектрисе угла.
Пусть дан угол со сторонами m и n и вершиной А. Возьмем произвольную точку D внутри угла таким образом, что перпендикуляры, опущенные из нее на стороны m и n угла А равны. Рассмотрим полученные треугольники ABD и ACD. Ð ABD = Ð ACD = 90°; BD = CD; AD – общая; D ABD = D ACD (как прямоугольные по гипотенузе и катету). Þ Ð BAD = Ð CAD Þ b – биссектриса Ð А. Определение 1. Пусть фигура имеет характерное свойство, определяющее, какие точки принадлежат фигуре. Тогда про эту фигуру говорят, что она является множеством точек, обладающих данным свойством или геометрическим местом точек, обладающих данным свойством. Определение 2. Биссектриса угла – это геометрическое место точек, равноудаленных от сторон угла. Определение 1. Прямая, перпендикулярная к отрезку и проходящая через его середину, называется серединным перпендикуляром к данному отрезку. Характерное свойство серединного перпендикуляра (прямая теорема). Каждая точка серединного перпендикуляра равноудалена от его концов.
Пусть дан отрезок АВ и серединный перпендикуляр к нему n, пересекающий отрезок АВ в точке С. Возьмем произвольную точку D на серединном перпендикуляре n и соединим ее с концами отрезка АВ отрезками AD и BD. Рассмотрим полученные треугольники A С D и В CD. Ð A С D = Ð В CD = 90°; АС = C В (n – серединный перпендикуляр); D С – общая; D A С D = D В CD (как прямоугольные по двум катетам). Þ А D = В D. Характерное свойство серединного перпендикуляра (обратная теорема). Точка, равноудаленная от концов отрезка, лежит на его серединном перпендикуляре. Доказательство:
Построим DC ^ AB. Рассмотрим полученные треугольники A С D и В CD. Ð A С D = Ð В CD = 90°; А D = В D (по условию); D С – общая; D A С D = D В CD (как прямоугольные по гипотенузе и катету). Þ АС = СВ. Определение 2. Пусть фигура имеет характерное свойство, определяющее, какие точки принадлежат фигуре. Тогда про эту фигуру говорят, что она является множеством точек, обладающих данным свойством или геометрическим местом точек, обладающих данным свойством. Определение 3. Серединный перпендикуляр к отрезку – это геометрическое место точек, равноудаленных от концов отрезка.
|
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 144; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.93.73 (0.02 с.) |
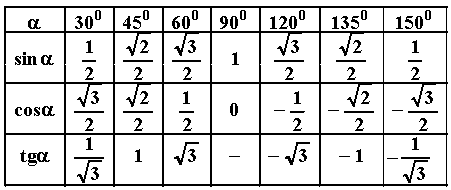
 - прямоугольный,
- прямоугольный,  =30
=30  ,
,  =60
=60 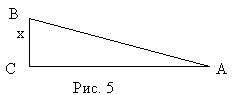
 АВ=2 x; sin30
АВ=2 x; sin30 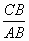 =
= 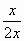 =
= 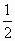 ;
; =
= 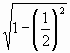 =
= 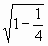 =
= 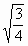 =
= 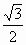 ;
;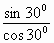 =
= 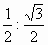 =
= 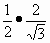 =
= 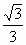 ;
;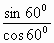 =
= 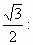
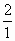 =
= 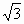 .
.
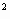 = x
= x 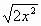 = x
= x 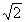 ;
;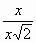 =
= 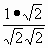 =
= 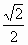 ; cos 45
; cos 45 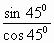 =
= 


