
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Состояние равновесия по НэшуСодержание книги
Поиск на нашем сайте
Определение 8. Стратегии
x Î C т.е. каждый игрок в ситуации х* получает свой наибольший выигрыш (в той мере, в какой это от него самого зависит). В рассмотренной игре “семейный спор” ситуации (А1,В1) и (А2,В2) являются решением по Нэшу, а в игре “дилемма заключенного” таковой является ситуация (А2,В2). В случае антагонистической игры равновесные стратегии игроков совпадают с их оптимальными стратегиями. Для неантагонистических игр понятие оптимальной стратегии игрока нередко вообще не имеет смысла: в таких играх оптимальными оказываются не стратегии отдельных игроков, а их сочетания (ситуации) и притом для всех игроков сразу. Поэтому в общих бескоалиционных играх оптимальными следует понимать совокупность действия всех игроков (ситуацию в игре), которая и является решением игры. Как и в играх двух лиц с нулевой суммой, игра N лиц с ненулевой суммой может не иметь решение по Нэшу в чистых стратегиях. Приведенное выше определение 7 решения по Нэшу в чистых стратегиях легко обобщается на случай смешанных стратегий путем подстановки смешанных стратегий Таким образом мы приходим к вероятностному распределению Х на множестве всех ситуаций. Другими словами, ситуация игры в смешанных стратегиях реализует различные ситуации в чистых стратегиях с некоторыми вероятностями. Значение функции выигрыша каждого из игроков оказывается случайной величиной. В качестве значения функции выигрыша принимается математическое ожидание этой случайной величины. Дж. Нэшем было доказано существование ситуации равновесия для любой конечной бескоалиционной игры. Теорема Нэша. В каждой бескоалиционной игре существует хотя бы одна ситуация равновесия в классе смешанных стратегий. Если, кроме того, функции Нi(х) выпуклые вверх, то решение по Нэшу достигается в классе чистых стратегий. Заметим, что принципиальная важность теоремы Нэша ограничивается существованием ситуации равновесия. Непосредственно применять ее для нахождения таких ситуаций не удается.
Дж. Нэшем была доказана также следующая теорема. Теорема 2. Конечная бескоалиционная игра имеет симметричные ситуации равновесия, в которых игроки, равноправно входящие в игру согласно ее условиям, фактически оказываются в одинаковом положении. Ее применение позволяет избежать отдельных ошибок при решении конечных бескоалиционных игр. Одним из простых классов бескоалиционных игр ход решения которых поддается элементарному описанию являются биматричные игры, представляющие собой бескоалиционную игру двух игроков с ненулевой суммой.
Описание биматричных игр Пусть в биматричной игре игрок 1 имеет m чистых А і,
Поэтому такие игры и называются биматричными. Используют также запись платежных матриц А и В в следующем виде:
где “северо-западное” число в каждой клетке обозначает выигрыш первого игрока, а “юго-восточное” – выигрыш второго игрока. Смешанные стратегии X и Y, естественно, понимаются как векторы, причем
Выигрыш игроков 1 и 2 при применении смешанных стратегий равны:
где Т – означает транспонирование, т.е. вектор строка записывается как вектор столбец; Определение ситуации равновесия для случая биматричной игры приобретает следующую формулировку. Ситуация (X,Y) в биматричной игре с матрицами выигрышей А и В является равновесной, если
Очевидно, что при В = -А биматричная игра превращается в матричную. В качестве примера рассмотрим биматричную игру «Торг». Пример. Игра «Торг» Игрок 1 продает неделимый товар игроку 2. Игрок 1 должен решить, какую назначить цену: высокую или низкую. Для покупателя в принципе приемлемы обе цены. Покупатель не может спорить о цене, он может либо сделать покупку, либо отказаться от нее. Платежные матрицы игроков имеют вид:
Описание всех возможных ситуаций в этой игре позволяет определить, что ситуация (А1, В1) является оптимальной по Парето и по Нэшу. Ситуация (А2, В2) также является оптимальной по Парето, но не является устойчивой, т.е. оптимальной по Нэшу. Рассмотрим способ нахождения устойчивых ситуаций для биматричных игр с произвольным количеством чистых стратегий игроков.
Решение биматричных игр Рассмотрим вначале биматричную игру 2х2 с матрицами выигрышей
соответственно игроков 1 и 2. Как и в случае матричных игр, смешанные стратегии полностью описываются вероятностями p и q выбора игроками своих первых чистых стратегий (вторые чистые стратегии выбираются, очевидно, с вероятностями 1-p и 1-q. Опишем порознь множество приемлемых ситуаций, для каждого из игроков и изобразим эти множества на единичном квадрате p, q, где pÎ[0,1] и qÎ[0,1]. Начнем с описания ситуаций, приемлемых в игре для игрока 1. Приемлемость ситуации (X,Y) для игрока 1 в биматричной игре означает, что
где А1 и А2 – вектор строки, соответствующие первой и второй строке матрицы А, соответственно. Подчеркнем, что эти условия приемлемости никак не связаны с матрицей В выигрышей игрока 2. Поэтому они будут совпадать с аналогичными условиями матричной игры с платежной матрицей А. Приемлемость ситуации (X,Y) для игрока 2 означает, что
где В1 и В2 – вектор-столбцы, соответствующие первому и второму столбцу матрицы В, соответственно. В общем случае, Х=Ip, 1 – pI. Рассмотрим три случая: а) р = 1, (Х=|1,0|). Тогда выражение (5.6) превращается в тождественное равенство, а условием приемлемости данной ситуации для игрока 1 оказывается неравенство (5.7). Для рассматриваемого случая его можно записать как
б) р = 0 (Х=|1,0|). В этом случае выражение (5.7) превращается в тождественное равенство, а условием приемлемости данной ситуации для игрока 2 оказывается неравенство (5.6). Для рассматриваемого случая оно имеет вид
в) 0< р <1 (Х=Ip, 1 - pI). В этом случае оба неравенства (5.6) и (5.7) превращаются в равенство, и условием приемлемости становится
Опишем ситуации приемлемости (5.10), (5.11) и (5.12) в развернутом виде. Так как
то соотношения (5.10), (5.11) и (5.12) можно соответственно записать как
Таким образом, приемлемые для игрока 1 ситуации (X,Y) могут быть одного из трех типов:
Неравенства (5.17) и (5.18) верны в случае, если а11 + а22 – а12 – а21 > 0. Если а11 + а22 – а12 – а21 < 0, то знак неравенства в соотношениях (5.17) и (5.18) необходимо поменять на противоположный. Если величина а11 + а22 – а12 – а21 = 0, а а22 – а12 ¹ 0, то (5.19) не имеет место, поэтому будет выполняться или (5.17) и (5.18), и притом со знаком строгого неравенства. Если же а11 + а22 – а12 – а21 = 0 и а22 – а12 = 0, то все условия (5.17), (5.18) и (5.19) выполняются тождественно, и приемлемыми для игрока 1 будут вообще все ситуации.
Описание ситуаций приемлемости в развернутом виде для игрока 2 получаем аналогично из неравенств (5.8) и (5.9). В общем случае Y=|q, 1-q|. Для трех случая получаем: а) q=1 (Y=|1,0|). В этом случае приемлемость ситуации (X,Y) равносильна неравенству
или в развернутом виде |p, 1-p|
б) q=0 (Y=|0,1|). В этом случае приемлемость ситуации (X,Y) определяется неравенством
или в развернутом виде
в) 0<q<1 (Y = |q,1–q|). Условие приемлемости
в развернутом виде
Таким образом, приемлемые для игрока 2 ситуации (X,Y) могут быть одного из трех типов:
Вновь подчеркнем, что неравенства (5.26) и (5.27) справедливы, если их знаменатель больше нуля. Если в11 + в22 – в12 – в21 < 0, то знак неравенства в выражениях (5.26) и (5.27) необходимо поменять на противоположный. Для определения ситуаций, приемлемых одновременно как для первого, так и для второго игроков, удобно все найденные приемлемые ситуации представить на единичном квадрате (рис. 5.3).
Рис. 5.3
Для случаев, когда а 11 + а 22 – а 12 – а 21 ¹ 0 и b 11 + b 22 – b 12 – b 21 ¹ 0 приемлемые ситуации игроков 1 и 2 составляют трехзвенные зигзаги. Причем, ситуации равновесия во вполне смешанных стратегиях игрока 2 совпадают с поведением игрока 2 в матричной игре с матрицей выигрыша А, а поведение игрока 1 – с поведением игрока 1 в матричной игре с матрицей выигрышей В. Таким образом, описанное равновесное поведение игроков оказывается ориентированным не столько на максимализацию собственного выигрыша, сколько на минимизацию выигрыша противника. Так, “антагонизм поведения” может возникнуть и при отсутствии “антагонизма интересов”. В приведенном на рис. 5.3 решении игры три ситуации равновесия, соответствуют точкам R1, R2, R3. Если бы зигзаги приемлемых ситуаций были одинаковой ориентации, как показано на рис. 5.4, то пересечение приемлемых ситуаций игрока 1 и игрока 2 состояло бы из одной точки R.
Рис. 5.4
При решении биматричных игр большей размерности необходимо решать большую систему линейных неравенств, определяемых выражениями (5.6), (5.7) и (5.8), (5.9), а затем таким же конечно-рациональным путем находить точки пересечения приемлемых ситуаций игрока 1 и игрока 2. Причем, любая конечная бескоалиционная игра имеет конечное и нечетное чисто ситуаций равновесия (решений игры). Поиск ситуаций равновесия в этом случае следует осуществлять с применением ПЭВМ.
Пример решения биматричной игры Формулировка игры “Борьба за рынки” Небольшая фирма (игрок 1) намерена сбыть крупную партию товара на одном из двух рынков, контролируемых другой, более крупной фирмой (игрок 2). Для этого оно может предпринять на одном из рынков соответствующие действия (например, развернуть рекламную кампанию). Господствующий на рынках игрок 2 может попытаться воспрепятствовать этому, предприняв на одном из двух рынков предупредительные меры. Игрок 1, не встретивший на рынке препятствий, захватывает его; встретившись с сопротивлением – терпит поражение. Выборы фирмами рынков являются их чистыми стратегиями. Пусть проникновение игрока 1 на первый рынок более выгодно для него, чем проникновение на второй, но борьба за первый рынок требует больших средств. Например, победа игрока 1 на первом рынке принесет ему вдвое больший выигрыш, чем на втором, но зато поражение на первом рынке полностью его разоряет (проигрыш равен 10), а игрока 2 избавляет от конкурента (выигрыш равен 5). Описанная биматричная игра может быть задана матрицами выигрышей
Решение игры. В соответствии с выражениями (5.6) и (5.7) приемлемыми ситуациями для игрока 1 будут те, которые удовлетворяют условиям
Рассмотрим три случая: а) р=1 (X=|1, 0|). В соответствии с выражением (5.10) имеем
Откуда б) р = 0 (X=|0, 1|). В соответствии с выражением (5.11) имеем
или в) 0< р <1 (X=| р, 1 – р |). В соответствии с выражением (5.12) или в развернутом виде (5.19) получаем
Приемлемые ситуации для игрока 2 в соответствии с выражениями (5.26), (5.27) и (5.27) следующие: а) б) в) Множества всех приемлемых ситуаций игрока 1 и игрока 2 изображены на рис. 5.5 (для игрока 2 соответствующее множество показано пунктиром).
Рис. 5.5 Зигзаги приемлемых ситуаций пересекаются в единственной точке
Цена игры для игрока 2
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-03-26; просмотров: 219; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.174.185 (0.008 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||

 ,
, 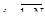 в игре N лиц с ненулевой суммой называются оптимальными по Нэшу (решением по Нэшу или точкой равновесия по Нэшу), если для каждого
в игре N лиц с ненулевой суммой называются оптимальными по Нэшу (решением по Нэшу или точкой равновесия по Нэшу), если для каждого 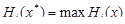 , (5.3)
, (5.3)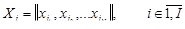 , представляющих собой вероятностное распределение на множестве чистых стратегий.
, представляющих собой вероятностное распределение на множестве чистых стратегий. , а игрок 2 имеет n чистых стратегий В j,
, а игрок 2 имеет n чистых стратегий В j, 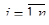 и в каждой ситуации (Ai, Bj) игрок 1 получает выигрыш aij, а игрок 2 – выигрыш bij. Значение обеих функций выигрыша игроков естественно представить в виде пары матриц
и в каждой ситуации (Ai, Bj) игрок 1 получает выигрыш aij, а игрок 2 – выигрыш bij. Значение обеих функций выигрыша игроков естественно представить в виде пары матриц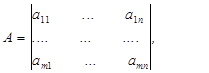
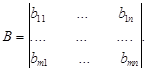
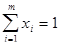 и
и 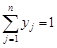 .
.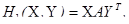
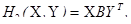
 - смешанные стратегии игроков 1 и 2 соответственно.
- смешанные стратегии игроков 1 и 2 соответственно.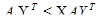
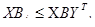
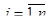 . (5.5)
. (5.5)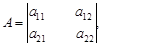
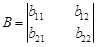 ,
,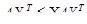 ; (5.6)
; (5.6)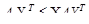 , (5.7)
, (5.7)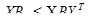 (5.8)
(5.8)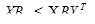 (5.9)
(5.9)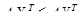 ; (5.10)
; (5.10)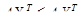 ; (5.11)
; (5.11)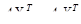 . (5.12)
. (5.12)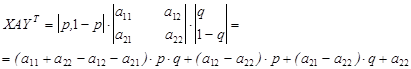
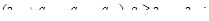 (5.14)
(5.14)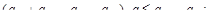 (5.15)
(5.15)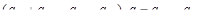 (5.16)
(5.16)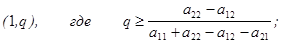 (5.17)
(5.17)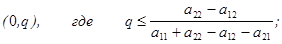 (5.18)
(5.18)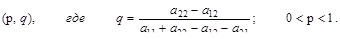 (5.19)
(5.19)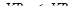 (5.20)
(5.20)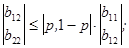
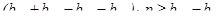 . (5.21)
. (5.21) (5.22)
(5.22)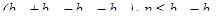 . (5.23)
. (5.23) (5.24)
(5.24)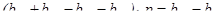 . (5.25)
. (5.25)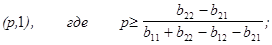 (5.26)
(5.26)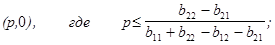 (5.27)
(5.27)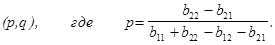 (5.28)
(5.28)
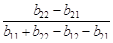
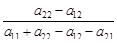


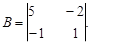
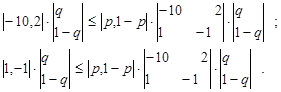
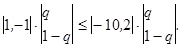
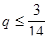 .
.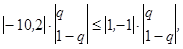
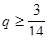 .
.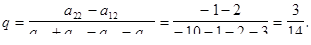
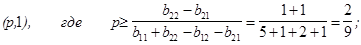
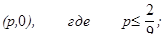
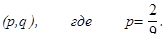

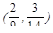 , которая и оказывается единственной ситуацией равновесия. Эта ситуация равновесия является ситуацией равновесия в смешанных стратегиях. Таким образом, оптимальными стратегиями по Нэшу являются
, которая и оказывается единственной ситуацией равновесия. Эта ситуация равновесия является ситуацией равновесия в смешанных стратегиях. Таким образом, оптимальными стратегиями по Нэшу являются 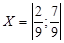 и
и 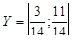 . При этом цена игры для игрока 1
. При этом цена игры для игрока 1 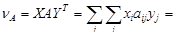
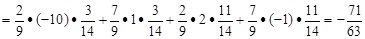 .
.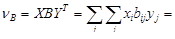
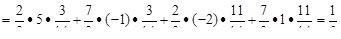 .
.


