
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение игр mхn. Эквивалентные задачи линейного программированияСодержание книги
Поиск на нашем сайте
Пусть имеется матричная игра mxn без седловой точки с матрицей выигрышей ||aij||. Допустим, что все выигрыши aij положительны (этого всегда можно добиться, прибавляя ко всем элементам матрицы достаточно большое число С; от этого, как уже отмечалось, цена игры увеличится на C, а оптимальные решения SA и SB не изменятся). Если все aij положительны, то и цена игры В соответствии с основной теоремой матричных игр, если платежная матрица не имеет седловой точки, то имеется пара оптимальных смешанных стратегий SA=||p1, p2,..., pm|| и SB=||q1, q2,..., qn||, применение которой обеспечивает игрокам получение цены игры Найдем вначале SA. Для этого предположим, что игрок В отказался от своей оптимальной смешанной стратегии SB и применяет только чистые стратегии. В каждом из этих случаев выигрыш игрока А будет не меньше, чем
Разделив левую и правую часть каждого из неравенств (2.25) на положительную величину v и введя обозначения:
запишем неравенства (2.25) в следующем виде:
где x1, x2,... xm - неотрицательные переменные. В силу того, что p1+p2+...+pm=1, переменные x1, x2,... xm удовлетворяют условию
Учитывая, что игрок А стремится максимизировать
min L (x)=x1+x2+... +xm. (2.29)
Из решения задачи линейного программирования находим цену игры
Аналогично находим оптимальную стратегию SВ игрока В. Предположим, что игрок А отказался от своей оптимальной стратегии SA и применяет только чистые стратегии. Тогда проигрыш игрока В в каждом из этих случаев будет не больше, чем
Разделив левую и правую части каждого их неравенств (2.32) на положительную величину
запишем неравенство (2.32) в следующем виде:
где y1, y2,..., yn - неотрицательные переменные. В силу того, что q1+q2+...+qn=1, переменные y1, y2,..., yn удовлетворяют условию
Учитывая, что игрок В стремится минимизировать положительную цену v (свой проигрыш), получаем задачу линейного программирования: найти неотрицательные значения переменных y1, y2,..., yn такие, чтобы они удовлетворяли линейным ограничениям (2.34) и обращали в максимум линейную функцию этих переменных:
max L (y)=y1+y2+... +ym. (2.36)
Эта задача является двойственной по отношению к задаче, представленной условиями (2.27) и (2.29). Оптимальная стратегия SB=||q1, q2,..., qn|| игрока В определяется из решения двойственной задачи линейного программирования по формулам:
Таким образом, оптимальные стратегии SA=||p1, p2,..., pm|| и SB=||q1, q2,..., qn|| матричной игры mxn с платежной матрицей ||aij|| могут быть найдены путем решения пары двойственных задач линейного программирования:
При этом
Пример. Найти решение и цену матричной игры, платежная матрица которой имеет вид
Решение
1. Так как 2. В данной игре нет дублирующих и доминируемых стратегий. 3. Решаем игру путем решения пары двойственных задач линейного программирования. Математические модели пары двойственных задач линейного программирования будут выглядеть следующим образом:
Данные задачи решаются, например, симплекс - методом. Поскольку в двойственной задаче ограничения имеют вид “£“, то эту задачу решать проще (не нужно вводить искусственные переменные). Оптимальное решение исходной задачи можно будет непосредственно получить из данных симплекс - таблицы для оптимального решения двойственной задачи. Начальная симплекс - таблица двойственной задачи имеет вид
Последующие симплекс-таблицы приведены ниже:
ведущий столбец
И, наконец, получаем симплекс-таблицу, которая соответствует оптимальному решению двойственной задачи:
Оптимальное решение двойственной задачи линейного программирования следующее: у1=
Находим оптимальную смешанную стратегию игрока В в соответствии с формулами (2.37) и (2.38):
Следовательно,
Оптимальное решение исходной задачи находим, используя двойственные оценки, из симплекс - таблицы для оптимального решения двойственной задачи: коэффициент при начальной базисной переменной в оптимальном уравнении прямой задачи равен разности между правой и левой частями ограничения двойственной задачи, ассоциированного с данной начальной переменной.
Получаем x1=
Отсюда определим вероятности применения своих активных стратегий игроком А:
Следовательно:
Таким образом, решение игры mxn сводится к решению задачи линейного программирования. Нужно заметить, что и наоборот, - для любой задачи линейного программирования может быть построена эквивалентная ей задача теории матричных игр. Эта связь задач теории матричных игр с задачами линейного программирования оказывается полезной не только для теории игр, но и для линейного программирования. Дело в том, что существуют приближенные численные методы решения матричных игр, которые при большой размерности задачи могут оказаться проще, чем симплекс - метод. ТЕСТЫ (В – Верно, Н – Неверно) 1. Если все элементы платежной матрицы в матричной игре положительны, то и цена игры положительна. 2. Любую матричную игру можно свести к паре двойственных задач линейного программирования. 3. В прямой задаче линейного программирования, к которой сводится матричная игра, целевая функция подлежит максимизации. 4. В обратной задаче линейного программирования, к которой сводится матричная игра, ограничения получаются со знаком « 5. Цена матричной игры, получаемая из решения прямой и обратной задач может быть различна.
Ответы: (1 - В; 2 - В; 3 - Н; 4 - В; 5 - Н).
ЗАДАЧИ Решить следующие матричные игры:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-03-26; просмотров: 319; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.008 с.) |

 при оптимальной стратегии тоже положительна, т.к.
при оптимальной стратегии тоже положительна, т.к. 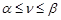 .
. .
. (2.25)
(2.25) (2.26)
(2.26) , (2.27)
, (2.27) . (2.28)
. (2.28) , получаем следующую задачу линейного программирования: найти неотрицательные значения переменных x1, x2,... xm такие, чтобы они удовлетворяли линейным ограничениям - неравенствам (2.27) и обращали в минимум линейную функцию этих переменных:
, получаем следующую задачу линейного программирования: найти неотрицательные значения переменных x1, x2,... xm такие, чтобы они удовлетворяли линейным ограничениям - неравенствам (2.27) и обращали в минимум линейную функцию этих переменных: , (2.30)
, (2.30)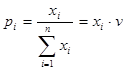 ,
, 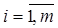 . (2.31)
. (2.31) . (2.32)
. (2.32)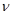 и введя обозначения:
и введя обозначения: , (2.33)
, (2.33) , (2.34)
, (2.34) . (2.35)
. (2.35) ,
, 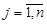 . (2.37)
. (2.37) ,
,
 ,
,  ;
;
 ,
,  .
.
 ,
,
 ,
,  ;
;
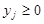 ,
, 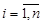 .
.
 , (2.38)
, (2.38) .
. Bj
Ai
Bj
Ai
 =1 не равно
=1 не равно  =3, то игра не имеет седловой точки.
=3, то игра не имеет седловой точки. 1;
2х 1+ х 2+3 х 3
1;
2х 1+ х 2+3 х 3 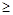 1;
3х 1+ х 2+ х 3
1;
3х 1+ х 2+ х 3  .
.
 1;
3y 1+y2+y3
1;
3y 1+y2+y3  1;
y 1+3y2+y3
1;
y 1+3y2+y3  .
.
 у4
у4
 у5
у5
 ведущий столбец
ведущий столбец

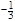


 у1
у1



 ведущий столбец
ведущий столбец



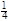
 у1
у1


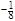
 L
L
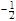
















 ; у2=
; у2= 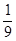 ; max L (y)=
; max L (y)=  .
. ;
; .
. .
. ; x2=
; x2=  ; x3=
; x3=  ; max L (x)=
; max L (x)=  .
. .
. .
. ».
».


