Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нормализация позиционной игрыСодержание книги
Поиск на нашем сайте
Процесс сведения позиционной игры к игре в нормальной форме называют нормализацией игры. Любая позиционная игра может быть сведена к игре в нормальной форме, в которой каждый из игроков делает только по одному независимому ходу. Для нормализации игры нужно перечислить все возможные стратегии игроков и для каждой совокупности стратегий определить выигрыш игроков. Рассмотрим процесс нормализации позиционной игры на конкретном примере. Пусть игра задана деревом, показанном на рис.3.5.
Рис. 3.5
Первый игрок делает свой первый ход, выбирая правую или левую ветвь. Затем ход делает второй игрок, у которого в каждой вершине также имеется два выбора, после чего игра заканчивается. В данной игре у первого игрока (игрока А) имеется две чистых стратегии: Ф1=/А1, А2/, где стратегия А1 - всегда выбирать левую ветвь; стратегия А2 - всегда выбирать правую ветвь. Второй игрок (игрок В) имеет больше стратегий: Ф2=/В1,В2,В3,В4/, где стратегия В1 - всегда выбирать левую ветвь; стратегия В2 - всегда выбирать правую ветвь; стратегия В3 - выбирать ветвь, которую выбрал игрок А; стратегия В4 - выбирать ветвь, противоположную той, которую выбрал игрок А. Матрица игры в этом случае имеет вид:
Очевидно, что исходная позиционная игра является игрой с полной информацией. Следовательно, она должна иметь седловую точку, а, следовательно, решение в чистых стратегиях. Действительно, так как
и, следовательно, Поэтому SA=||1,0|| или SA=||0,1||, а SB=||0,0,0,1||. Цена игры v =-2. Допустим, что в рассматриваемом примере второму игроку не сообщается выбор, сделанный первым игроком. Тогда в дереве игры на втором ходе появляется класс информации V 1, содержащей две вершины второго игрока (рис.3.6)
Рис. 3.6 Количество чистых стратегий второго игрока по сравнению с первым случаем сократится до двух: Ф2=/В1,В2/, где В1 - всегда выбирать левую ветвь; В2 - всегда выбирать правую ветвь. Процесс нормализации приводит к следующей платежной матрице:
В новой игре a¹b, т.е. седловая точка отсутствует. Решение игры в смешанных стратегиях имеет вид:
Уменьшение информации, имеющейся у второго игрока на момент принятия решения, привело к уменьшению его выигрыша с 2 до Итак для нормализации позиционной игры необходимо: * перечислить все возможные стратегии каждого из игроков (в таких играх, как шахматы, это пока неразрешимая задача); * определить исходы игры при всех возможных сочетаниях стратегий игроков (выборы стратегий делаются игроками одновременно и независимо). В зависимости от количества игроков, а также значений их выигрышей путем нормализации позиционные игры можно свести к матричной или бескоалиционной, в частности, биматричной игре, каждые из которых решаются по-своему.
ТЕСТЫ (В – Верно, Н – Неверно) 1. В позиционных играх каждый из игроков может делать по несколько ходов, причем информация о прошедшем может меняться от хода к ходу. 2. Позиционные игры не могут включать случайные ходы. 3. Дерево позиционной игры имеет не более одного корня и не менее одной вершины. 4. Из корня дерева позиционной игры к какой-нибудь его вершине могут быть несколько путей. 5. Если все классы информации позиционной игры содержат только по одной вершине, то такая игра является игрой с неполной информацией. 6. Классы информации должны содержать вершины только одного игрока. 7. Вершины класса информации могут соответствовать различным временным ходам. 8. Из всех вершин, составляющих класс информации, может выходить только одинаковое количество ветвей. 9. Любая позиционная игра может быть сведена к игре в нормальной форме. 10. Игры с полной информацией имеют седловую точку и решаются в чистых стратегиях. 11. Теорема Куна утверждает, что позиционная игра с полной информацией разрешима по доминированию. 12. Для нормализации позиционной игры необходимо перечислить все возможные стратегии каждого из игроков и определить все возможные исходы игры.
(Ответы: 1-В; 2-Н; 3-В; 4-Н; 5-Н; 6-В; 7-Н; 8-В; 9-В; 10-В; 11-В; 12-В.)
ЗАДАЧИ
І. Произвести нормализацию позиционных игр, у которых дерево игры имеет вид, приведенный ниже. У конечных вершин поставлен выигрыш первого игрока, а выигрыш второго игрока противоположен по знаку. Варианты:
1.
2.
3.
4.
2. Нарисовать дерево следующей позиционной игры «Выбор с правом вето», у которой N игроков выбирают одного кандидата из множества
Варианты: 1. N =2; u1={2,-5,4}; u2={-2,5,-4} 2. N =2; u1={2,5,-4,-3,1}; u2={-2-3,4,3,-1} 3. N =3; u1={1,2,-3,4}; u2={3,2,1,-5}; u3={-2,-3,-1,8}. 4. N =4; u1={1,2,-2,-3,4}; u2={3,5,1,-7,6}; u3={2,4,-5,-1,1}; u4={2,3,4,1,6}.
|
||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-03-26; просмотров: 740; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.36.36 (0.007 с.) |



 ;
; .
. .
.

 .
. .
.


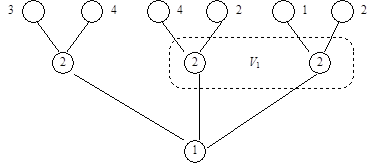
 , i < N. Правило голосования таково: начиная с игрока 1, каждый игрок последовательно налагает вето на выбор кандидатуры одного из не отведенных кандидатов. Единственный оставшийся кандидат считается избранным. Заданы также функции выигрыша u1, u2, …, uN на множестве С, т.е. выигрыш каждого игрока в зависимости от того, какой кандидат победил. Найти решение, используя теорему Куна.
, i < N. Правило голосования таково: начиная с игрока 1, каждый игрок последовательно налагает вето на выбор кандидатуры одного из не отведенных кандидатов. Единственный оставшийся кандидат считается избранным. Заданы также функции выигрыша u1, u2, …, uN на множестве С, т.е. выигрыш каждого игрока в зависимости от того, какой кандидат победил. Найти решение, используя теорему Куна.