
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принцип максимина в антагонистических играх. Седловая точкаСодержание книги
Поиск на нашем сайте
Как отмечалось, важнейшим вопросом в теории игр (в том числе и матричных) является вопрос о выборе оптимальных стратегий для каждого из игроков. Оптимальной стратегией игрока в матричной игре называется такая, которая обеспечивает ему максимальный выигрыш. Если игра повторяется неоднократно, то оптимальная стратегия должна обеспечивать максимальный средний выигрыш. При выборе этой стратегии основой рассуждений является предположение, что противник является, по меньшей мере, так же разумен, как и мы сами, и делает все, чтобы добиться такой же цели. Расчет на разумного противника - лишь одна из возможных позиций в конфликте, но в теории игр именно она кладется в основу. При этом для выбора оптимальной стратегии используют принцип максимина: выбирай ту стратегию, чтобы при наихудшем для нас поведении противника получить максимальный выигрыш. Другими словами, принцип максимина предполагает выбор той стратегии, при которой наш минимальный выигрыш для различных стратегий максимален. Отсюда и название «принцип максимина». Как видно, принцип максимина - это принцип крайне осторожного игрока, но именно он является основным принципом теории матричных игр. Для пояснения принципа максимина рассмотрим пример 1 матричной игры G (4х5) с платежной матрицей, приведенной на рис. 2.2. Пример 1.
Рис. 2.2 Какой стратегией игроку А воспользоваться? Есть соблазнительный выигрыш 12, при применении стратегии А 3. Но при этом противник может выбрать стратегию В 3, и игрок А получит выигрыш, равный всего трем. Для определения оптимальной стратегии в соответствии с принципом максимина, запишем в правом добавочном столбце платежной матрицы минимальное значение a i в каждой строке (минимум строки). Из всех значений a i (правый столбец) выделим наибольшее. Ему соответствует стратегия А 4. Выбрав эту стратегию, мы во всяком случае можем быть уверены, что при любом поведении противника выигрыш будет не менее пяти. Эта величина - наш гарантированный выигрыш. Он называется нижней ценой игры (или «максимином» - максимальный из минимальных выигрышей). Будем обозначать его a. В нашем примере a = Теперь станем на точку зрения игрока В и порассуждаем за него. Выбирая стратегию, он хотел бы отдать поменьше, но должен рассчитывать на наихудшее для него поведение игрока А. Припишем к платежной матрице (рис.2.2) нижнюю строку и в ней запишем наихудшее для игрока В возможные результаты (максимумы столбцов b j. Очевидно, осторожный противник должен выбрать стратегию, при которой величина b j минимальна. Эта величина называется верхней ценой игры (или “минимаксом” - минимальный из максимальных проигрышей). Будем обозначать ее b. В нашем примере b = Итак, исходя из принципа осторожности, игрок А должен выбрать стратегию А 4, а его противник - В 3. Такие стратегии называются максиминными или минимаксными стратегиями (вытекающие из принципа максимина). До тех пор, пока обе стороны в нашем примере будут придерживаться своих максиминных стратегий, выигрыш игрока А и проигрыш игрока В будет равен а 43=5. Легко показать, что нижняя цена игры никогда не превосходит верхней цены игры. Лемма 1. Пусть задана матрица выигрышей А = êêaijêêи определены b= Тогда Доказательство. По определению максимума и минимума для любых фиксированных значений i и j имеем
Поскольку левая часть неравенства (2.1) не зависит от i, то можем записать
Так как правая часть неравенства (2.1) не зависит от j, то
Объединяя неравенства (2.2) и (2.3), получаем неравенство (2.1), что и требовалось доказать. Итак, всегда b ³ a. Случай b = a, соответствует наличию у платежной матрицы так называемой седловой точки. Определение. Точка (i *, j *) называется седловой точкой платежной матрицы || a ij||, если для всех остальных i и j этой матрицы выполняется условие ai*j ³ai*j*³ aij*, т.е. аij является одновременно минимумом своей строки и максимумом своего столбца. Приведем без доказательства следующую теорему.
Теорема 1. Для того чтобы
необходимо и достаточно, чтобы матрица || a ij|| имела седловую точку. Кроме того, если (i *, j *) - седловая точка матрицы || a ij||, то
Говорят, что матричная игра имеет седловую точку, если соответствующая ей матрица выигрышей (платежная матрица) имеет седловую точку.
Пример 2. Найти решение игры G (3х3), платежная матрица которой имеет следующий вид:
Определим Нижняя цена игры Верхняя цена игры Так как a=b=0, то платежная матрица и матричная игра имеют седловую точку. Оптимальными стратегиями для игрока А является стратегия А3, а для игрока В - В3. Легко заметить, что отклонение игрока А от оптимальной стратегии приводит к уменьшению его выигрыша, а одностороннее отклонение игрока В - к увеличению его проигрыша. Могут встречаться случаи, когда платежная матрица имеет несколько седловых точек, однако это не изменит характера рекомендуемых решений, поскольку все ситуации равновесия имеют одну и ту же цену, а следовательно, эквиваленты.
Пример 3. Найти решение игры G (3х4), платежная матрица которой имеет вид:
Определим a i и bj и запишем их в таблицу. Находим нижнюю и верхнюю цену игры:
В заключение отметим, что с позиций игрока 1 второй игрок руководствуется принципом минимакса, обеспечивающим минимизацию максимальных потерь. Но с собственной точки зрения игрока 2, оценивающего свой выигрыш, он также руководствуется принципом максимина. Поэтому, как правило, говорят лишь об использовании в антагонистической игре принципа максимина обоими игроками. ТЕСТЫ (В – Верно, Н – Неверно)
1. Матричная игра является антагонистической, поскольку выигрыш одного игрока равен проигрышу второго (выигрышу второго с обратным знаком). 2. Название “матричная игра” произошло из-за того, что такая игра описывает платежной функцией в виде матрицы. 3. В матричной игре каждый из игроков делает свой ход независимо от хода противника, предполагая лишь, что противник разумен, как и он сам. 4. Оптимальной стратегией игрока в матричной игре называется такая, которая обеспечивает ему максимальный средний выигрыш. 5. Принципом максимина руководствуются очень азартные и рискованные люди (оптимисты). 6. Принцип максимина предполагает выбор той стратегии, при которой минимальный выигрыш для различных стратегий максимален. 7. Стратегии, выбираемые из принципа максимина, называются максиминными. 8. Нижняя цена матричной игры всегда равна верхней цене. 9. Случай, когда нижняя цена матричной игры равна верхней цене, соответствует наличию у платежной матрицы седловой точки. 10. Платежная матрица игры не может иметь несколько седловых точек. 11. Если платежная матрица игры содержит седловую точку, то ее решение сразу находится по принципу максимина.
(Ответы: 1-В; 2-В; 3-В; 4-В; 5-Н; 6-В; 7-В; 8-Н; 9-В; 10-Н; 11-В.)
ЗАДАЧИ 1. Составьте платежную матрицу игры Морра, если в ней участвуют два игрока, а максимально возможное количество «выбрасываемых» пальцев равно i (i =2,3,4,5,6,7,8,9,10). Выигрыш равен сумме пальцев выброшенных игроками. При четной сумме выигрывает первый игрок, при нечетной – второй. 2. Составьте платежную матрицу игры борьба за рынки, если фирма А имеет в своем распоряжение а условных денежных единиц, а противник - в. а=3,4,5,6,7,8,9,10; а соответствующие в=2,3,4,5,6,7,8,9. 3. Найдите седловую точку и максиминные стратегии игроков для следующих матричных игр:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-03-26; просмотров: 322; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.200.151 (0.007 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 Bj
Ai
Bj
Ai
 A4
A4
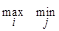 aij
aij
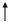
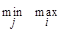 aij
aij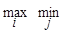 aij =5.
aij =5.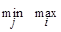 aij = 7.
aij = 7.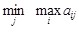 и a=
и a= 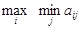 .
.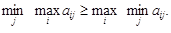 .
.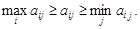 (2.1)
(2.1)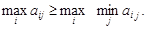 (2.2)
(2.2)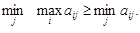 (2.3)
(2.3)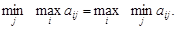
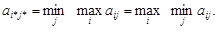 (2.4)
(2.4)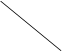 Bj
Ai
Bj
Ai
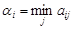 и
и 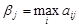 и запишем их в таблицу.
и запишем их в таблицу.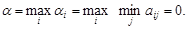
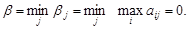
 Bj
Ai
Bj
Ai
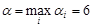 ;
; 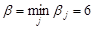 . Видно, что игра имеет четыре седловые точки с соответствующими парами оптимальных стратегий: А1В2; А1В4; А3В2 и А3В4. Цена игры равна 6.
. Видно, что игра имеет четыре седловые точки с соответствующими парами оптимальных стратегий: А1В2; А1В4; А3В2 и А3В4. Цена игры равна 6.


