
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные теоремы матричных игр
Если игрок А выбирает смешанную стратегию SA=||p1, p2,..., pm||, а игрок В смешанную стратегию SB=||q1, q2,..., qn||,то средний выигрыш математическое ожидание выигрыша игрока А (проигрыша игрока В) определится суммой
которая может рассматриваться в качестве характеристики выбранных SА и SB. Формируя свою стратегию SА в антагонистической игре, игрок А в соответствии с принципом максимина должен выбрать такую стратегию, при которой минимально возможный выигрыш был бы максимален, т.е. такую стратегию, которая обеспечивает
Аналогичные рассуждения, связанные с поиском оптимальной смешанной стратегии игрока В, приводят к рекомендации выбрать такую стратегию SB, которая обеспечивает
Весьма важным для теории и практики является вопрос о том, связаны ли между собой v А и v B. Ответ на него дает теорема о максимине. Теорема о максимине. В конечной игре двух игроков (коалиций) с нулевой суммой (матричной игре) при
Теорема о максимине указывает на существование равновесия для случая v А= v B, при Поэтому другая формулировка теоремы о максимине, называемая основной теоремой матричных игр определяется следующим образом.
Основная теорема матричных игр. Любая матричная игра имеет, по крайней мере, одно оптимальное решение, в общем случае, в смешанных стратегиях и соответствующую цену v. Обе эти теоремы эквивалентны. Из этих теорем следует, что любая матричная игра имеет цену v. Цена игры v - средний выигрыш, приходящийся на одну партию, - всегда удовлетворяет условию a£n£b, (2.10) т.е. лежит между нижней a и верхней b ценами игры. Оптимальное решение игры в смешанных стратегиях, также как и решение в чистых стратегиях, обладает тем свойством, что каждый из игроков не заинтересован в отходе от своей оптимальной смешанной стратегии, если его противник применяет свою оптимальную смешанную стратегию, так как это ему невыгодно. Эта пара стратегий образует в игре положение равновесия: один игрок хочет обратить выигрыш в максимум, другой - в минимум, каждый “тянет” в свою сторону и, при оптимальном поведение обоих, устанавливается равновесие и устойчивый выигрыш n.
Определение. Те из чистых стратегий игроков А и В, которые входят в их оптимальные смешанные стратегии с вероятностями, не равными нулю, называются активными стратегиями. Существует теорема об активных стратегиях, применение которой позволяет упрощать решение некоторых матричных игр. Теорема об активных стратегиях. Если один из участников матричной игры G (m x n), придерживается своей оптимальной смешанной стратегии, то это обеспечивает ему максимальный средний выигрыш, равный цене игры n, независимо от того, какие действия предпринимает другой игрок, если только он не выходит за пределы своих активных стратегий (т.е. пользуется любой из них в чистом виде или смешивает их в любых пропорциях), причем число активных стратегий каждого игрока, входящих в их оптимальные смешанные стратегии, не превосходит L, где L = min(m, n). Использование данной теоремы позволяет в частности, упрощать решение матричных игр 2 x n и m x 2.
ТЕСТЫ (В – Верно, Н – Неверно) 1. В антагонистической игре пара стратегий (A i, B j) называется равновесной или устойчивой, если ни одному из игроков не выгодно отходить от своей стратегии. 2. Стратегии, соответствующие седловой точке платежной матрицы, не обладают свойством равновесия (устойчивости). 3. Игра решается в чистых стратегиях если платежная матрица имеет седловую точку. 4. Игра решается в чистых стратегиях, если нижняя цена платежной матрицы равна верхней. 5. Игры с полной информацией всегда имеют седловую точку. 6. Случайная величина, значениями которой являются чистые стратегии игрока, называется его смешанной стратегией. 7. Если игрок А применяет смешанную стратегию SA=||p1, p2,..., pm||, а игрок В смешанную стратегию SB=||q1, q2,..., qn||, то средний выигрыш игрока А определяется соотношением 8. Если матричная игра не имеет седловой точки, то игроки должны использовать оптимальные смешанные стратегии. 9. Оптимальные смешанные стратегии в отличие от оптимальных чистых стратегий не обладают свойством равновесия (устойчивости). 10. Те из чистых стратегий игроков, которые входят в их оптимальные смешанные стратегии с вероятностями, не равными нулю, называются активными стратегиями.
11. Любая, матричная игра имеет по крайней мере, одно оптимальное решение, в общем случае, в смешанных стратегиях и соответствующую цену n. 12. Теорема о максимине утверждает, что
13. При оптимальных смешанных стратегиях цена игры n удовлетворяет условию a£n£b. 14. Теорема об активных стратегиях утверждает, что если игрок придерживается свой оптимальной смешанной стратегии, то это обеспечивает ему максимальный средний выигрыш, независимо от того, какие действия предпринимает другой игрок, если только тот не выходит за пределы своих активных стратегий.
(Ответы: 1-В; 2-Н; 3-В; 4-В; 5-В; 6-В; 7-Н; 8-В; 9-Н; 10-В; 11-В; 12-В; 13-В; 14-В.)
|
||||||
|
Последнее изменение этой страницы: 2020-03-26; просмотров: 76; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.252.140 (0.006 с.) |
 ,
, (2.7)
(2.7)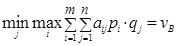 . (2.8)
. (2.8) имеет место равенство
имеет место равенство . (2.9)
. (2.9)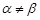 и, следовательно, существования оптимальных смешанных стратегий.
и, следовательно, существования оптимальных смешанных стратегий.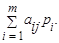
 .
.


