
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классификация методов глобальной оптимизацииСодержание книги
Поиск на нашем сайте Использование двухэтапного алгоритма весовой фильтрации предполагает на первом этапе применение процедуры, обеспечивающей поиск точки (области) глобального экстремума -
Последнее неравенство устанавливает интересный парадокс [8]: если глобальный минимум Для того чтобы использовать полученную о целевой функции информацию и рационально планировать процесс поиска, в глобальной оптимизации используется термин «модель многоэкстремальной целевой функции» [11,13]. При этом с одной стороны, желательно иметь достаточно общую модель, охватывающую возможно большее число возникающих на практике задач. С другой стороны, модель должна быть достаточно определенной, чтобы обеспечить эффективность построенных на ее основе алгоритмов. Ряд алгоритмов глобальной оптимизации обобщают известные локальные методы. В этом случае в качестве модели принимается класс дифференцируемых или дважды дифференцируемых функций [8]. Применение алгоритмов, основанных на этой модели, к решению практических задач синтеза сталкивается с трудно решаемой проблемой оценки границ производных [12]. Если оценка завышена, то для получения приемлемой оценки глобального минимума может потребоваться огромное количество вычислений целевой функции. Если же оценка занижена, то из рассмотрения может быть исключена подобласть, фактически содержащая глобальный минимум. При этом большинство методов этого класса строятся согласно принципу минимакса [8]. Алгоритм глобальной оптимизации считается оптимальным в минимаксном смысле, если он позволяет максимально быстро отыскивать минимум наихудшей функции. Но пользователи алгоритмов оптимизации часто стремятся к эффективности в среднем, для их типичной задачи, а не для какого-то редко встречаемого на практике случая. Стремление сформулировать математическую задачу глобальной оптимизации, соответствующей практической ситуации, привело к введению статистической модели многоэкстремальных функций [17]. В рамках статистической модели алгоритмы глобальной оптимизации строятся по критерию средней эффективности. Согласно этому критерию алгоритм считается оптимальным, если он позволяет максимально быстро отыскивать минимум типичного (среднего) представителя рассматриваемого класса функций. Алгоритмы глобальной оптимизации в настоящее время принято разделять на два класса [11,13,17]: использующие модель глобального поведения функции (рациональные) и не использующие таковой (эвристические). Наиболее яркими представителями рациональных алгоритмов являются минимаксные и оптимальные в среднем алгоритмы. К первым относятся алгоритмы минимизации функций с ограниченной скоростью изменения. Другой подход к принятию рациональных решений в условиях неопределенности основан на применении статистических моделей. Сюда же можно отнести и декомпозиционные методы, использующие как идеи минимаксных алгоритмов, так и критерий средней рациональности. Общим для рациональных алгоритмов является сложность вспомогательных вычислений [8]. Наиболее яркими представителями эвристических алгоритмов являются глобальные обобщения локальных (многократный локальный спуск из случайных точек или чередование спуска в локальный минимум с подъемом в седловую точку). Кроме этого, многие эвристические алгоритмы используют случайный поиск, то есть точки Основные идеи построения рациональных и эвристических алгоритмов определяют следующую классификацию [11,17]: 1. Методы поиска глобального экстремума, основанные на использовании алгоритмов локальной оптимизации. 2. Алгоритмы минимизации функций с ограниченной скоростью изменения. 3. Методы, основанные на использовании статистических моделей целевых функций. 4. Глобальный случайный поиск. 5. Методы декомпозиции. Анализ большого количества работ [8,11,17], посвященных методам глобальной оптимизации показывает, что с точки зрения объема вычислительных затрат, точности нахождения глобального экстремума и возможности программной реализации наиболее предпочтительными являются алгоритмы глобального случайного поиска и методы декомпозиции.
|
||
|
Последнее изменение этой страницы: 2020-03-13; просмотров: 245; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 . Математическая формулировка этого факта имеет следующую форму [8]:
. Математическая формулировка этого факта имеет следующую форму [8]: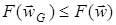 при всех
при всех  .
. генерируются случайно (метод Монте-Карло). Но, для того чтобы вероятность нахождения глобального минимума сделать близкой к единице, количество точек
генерируются случайно (метод Монте-Карло). Но, для того чтобы вероятность нахождения глобального минимума сделать близкой к единице, количество точек 


