
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача пространственно-временной обработки изображений при наличии шумов и помехСодержание книги
Поиск на нашем сайте
Введение
Характерной тенденцией развития современных систем обработки изображений вне зависимости от их целевого назначения, является повышение требований к эффективности и качеству мониторинга территории Земли, а также объектов и явлений космического и воздушного пространства при наличии шумов и помех. Решение этих задач диктует необходимость совершенствования математических и программных средств пространственно-временной фильтрации изображений. Пространственно-временная фильтрация изображений - совокупность операций по преобразованию изображения, позволяющая осуществить выделение искомого объекта среди других мешающих. С более общей точки зрения, пространственная фильтрация изображений представляет собой важнейшую подготовительную операцию максимизации отношения сигнал / помеха при распознавании объекта, облегчающую принятие решении о наличии и положении искомого объекта в поле изображения. Основу современных методов пространственно-временной фильтрации изображений составляют высококачественные средства ввода изображений и эффективные численные алгоритмы пространственно-временной фильтрации изображений при наличии помех и шумов. С точки же зрения подготовки специалистов, основой закрепления теоретического курса «Проектирования РЭС» является лабораторный практикум. Поэтому разработка лабораторного программного комплекса для исследования эффективности пространственно-временной обработки изображений является важной и актуальной задачей. Данный дипломный проект посвящен разработке лабораторной работы №1 по дисциплине «Проектирование РЭС», целью которой служит исследование эффективности весовой пространственно-временной обработки изображений с использованием статистик среднего ранга при наличии белого шума и импульсных помех. 1.
Традиционно в вузовском образовании лабораторный практикум основывался на аппаратной технологии, позволяющей проводить исследования изучаемых процессов, принципов и закономерностей, устройств и систем на базе лабораторных макетов и измерительных приборов. Постановка новых работ с использованием лабораторных стендов и макетов требует значительных затрат на разработку и изготовление самих стендов, комплектацию рабочих мест контрольно-измерительным оборудованием и тому подобное. В связи с этим перспективным является внедрение в лабораторный практикум элементов программного моделирования. Программа цикла лабораторных работ по курсу «Проектирование РЭС» рассчитана на работу в лаборатории, которая укомплектована рабочими местами, оснащенными ПЭВМ. Эти ПЭВМ, в свою очередь, объединены в локальную сеть для облегчения установки программного обеспечения на рабочие места. Разработанный в данном дипломном проекте программные блок позволит заменить дорогостоящие лабораторные установки, следовательно, для введения нового цикла лабораторных работ не потребуется закупка дополнительного оборудования. Таким образом, затраты на введение курса лабораторных работ сводятся к затратам на проектирование курса и обслуживание лаборатории. Применение персональных ЭВМ (электронных вычислительных машин) в лабораторном практикуме для исследования систем автоматического управления дает возможность выполнить: · анализ функционирования системы в различных режимах с учетом разброса параметров элементов и наличия дестабилизирующих факторов; · синтез структуры и принципиальной схемы устройств; · параметрическую оптимизацию, при этом удается избежать трудоемкого и дорогостоящего этапа макетирования. Опыт совместного проведения работ по типовой и компьютерной методикам подтвердил высокую эффективность данной технологии, помогающей студентам быстрее и лучше осваивать изучаемые разделы программы. 2.
Временная фильтрация При временной фильтрации изображений рассматривается последовательность кадров изображения
Рисунок 2.2 - Схема временной фильтрации изображений
Процесс временной фильтрации состоит в том, что апертура
С учетом этого соответствующие выражения для фильтров, определяемых соотношениями (2.1-5) - (2.1-10), при временной фильтрации принимают следующий вид:
- среднеарифметический фильтр: - среднегеометрический фильтр: - среднегармонический фильтр: - среднеконтргармонический фильтр: - медианный фильтр: - псевдомедианный фильтр: - минимальный фильтр: - максимальный фильтр:
Необходимо отметить, что, как и в случае пространственной фильтрации, для повышения эффективности временной фильтрации, то есть для уменьшения квадрата СКО вида (2.1-3), используется весовая временная фильтрация, которая задается выражением вида:
где Весовая временная фильтрация осуществляется таким же способом, что и пространственная. При движении маски по полю кадров, в каждом ее положении весовая функция
Глобальный случайный поиск Исторически первым и довольно долгое время единственным широко используемым методом поиска глобального экстремума являлся метод, названный впоследствии «мультистарт». Этот метод состоит в многократном (последовательном или параллельном) отыскании локальных минимумов из различных начальных точек, чаще всего случайных (такой вид алгоритма носит название «случайный мультистарт») [8]. Использование случайного выбора при построении алгоритмов глобальной оптимизации приводит к алгоритмам глобального случайного поиска [17]. Основными причинами популярности методов случайного поиска среди пользователей являются следующие. Структура алгоритмов довольно проста, и их можно легко реализовать в виде программ ЭВМ. Алгоритмы робастны, то есть малочувствительны к нерегулярностям поведения целевой функции, структуры множества оптимизации, наличию случайных ошибок при вычислении функции; кроме того, они малочувствительны к росту размерности множества оптимизации. Наконец, в рамках известных схем случайного поиска легко строятся новые алгоритмы, реализующие различные эвристические процедуры адаптации. Разработано большое разнообразие методов глобального случайного поиска [17]. В основе построение этих алгоритмов лежит следующая общая схема: Выбирается некоторое распределение вероятностей Моделируется некоторое число раз Согласно определенному правилу конструируется распределение вероятностей Проверяется условие останова, и если оно не выполняется, то осуществляется переход к шагу 2 с заменой Таким образом, любой алгоритм глобального случайного поиска состоит из некоторого числа итераций, на каждой из которых моделируется специальным образом сконструированные распределения. К сожалению, для алгоритмов глобального случайного поиска нет повода испытывать оптимизм. Причины для этого следующие [17]. Во-первых, хотя большинство методов обладает теоретическим свойством сходимости, оценки этой скорости сходимости показывают, что она крайне медленная. Во-вторых, методы случайного поиска, обладающие наибольшей практической эффективностью, содержат в себе элементы эвристики и поэтому обладают недостатком, присущим эвристическим методам: нечетко определен класс задач, для которых методы эффективны; отсутствуют четкие рекомендации о выборе параметров методов, а эти параметры в значительной степени влияют на эффективность. В-третьих, как показывают численные и теоретические результаты, только за счет усложнения алгоритма и уменьшения доли случайности можно повысить его эффективность. Следовательно, применение алгоритмов глобального случайного поиска при решении задачи весовой фильтрации наиболее рационально для минимизации функций, вычисление которых не требует значительных затрат машинного времени. Методы условной оптимизации В задачах весовой пространственно-временной фильтрации всегда имеет место наличие ограничений, накладываемых на вектор весовых коэффициентов
где
Ограничения значительно усложняют процесс оптимизации и приводят к необходимости решения задач условной минимизации. Наличие эффективных алгоритмов безусловной оптимизации дает возможность их применения в задачах с ограничениями. В этом случае целевая функция должна быть модифицирована так, чтобы она оставалась почти неизменной внутри допустимой области, но резко возрастала при подходе к границам, задаваемым ограничениями. Последнего можно добиться, если назначить штрафную функцию по каждому из ограничений. Тогда вспомогательная функция будет иметь следующий вид [17]:
где В методах барьерных функций
где r - положительное число, а
Она определена внутри W и неограниченно возрастает, если логарифмическая функция обратная функция Чем меньше значение r, тем меньше влияние второго слагаемого в выражении для Модельная схема оптимизации в этом случае формулируется так [17]: Выбирается монотонно убывающая сходящаяся к нулю последовательность
Начиная с точки Доказано, что последовательность безусловных минимумов функции Непосредственное применение стандартных алгоритмов безусловной минимизации функции Таким образом, рассмотренные методы барьерных функций, построенные на базе эффективных алгоритмов безусловной минимизации, являются наиболее перспективными для решения задач весовой пространственно-временной фильтрации. Критерии останова Поскольку методы оптимизации носят итерационный характер, то при их практической реализации возникает задача определения специальных правил прерывания счета - критериев останова. Как правило, процесс оптимизации прекращается, если: 1 достигнута требуемая точность решения; 2 хорошее приближение еще не найдено, но скорость движения к минимуму так упала, что не имеет смысла продолжать счет; 3 метод начал расходится или зациклился. Этим условиям удовлетворяют следующие критерии останова, используемые в работе [11,16,17]:
Приведенные неравенства отражают признаки близости последовательностей
3.
Результатом дипломного проекта стала рабочая версия программы пространственно-временной обработки изображений STIP32, обобщённая структурная схема которой приведена на рисунке 3.1. Программа состоит из трёх частей. Разработанный доцентом кафедры РУС Смирновым А.А. графический интерфейс пользователя (Graphical User Interface - GUI), в основу которого положена система окон и стандартных средств ввода / вывода информации (меню, таблицы, кнопки, радиокнопки, переключатели, строки ввода, списки и так далее), осуществляет взаимодействие с блоком ввода / вывода информации.
Рисунок 3.1 - Обобщенная структурная схема программы пространственно-временной обработки изображений
Главная программа включает в себя три основных блока: блок ввода / вывода информации, блок фильтрации изображений и блок оптимизации, взаимодействующий с библиотекой алгоритмов оптимизации. Все приведенные блоки взаимосвязаны друг с другом и образуют единую полноценную систему обработки изображений. В блок ввода / вывода информации поступают соответствующие данные от пользователя, который устанавливает необходимые параметры (вид фильтра и фильтрации, размер апертуры, СКО белого шума, вероятности Структурная схема блока фильтрации изображений приведена на рисунке 3.2.
Рисунок 3.2 - Структурная схема блока фильтрации изображений
Библиотеки пространственных и временных фильтров включают в себя следующие типы фильтров: 1. Среднеарифметический. 2. Среднегеометрический. 3. Среднегармонический. 4. Среднеконтргармонический. 5. Медианный. 6. Модифицированный медианный. 7. Минимальный. 8. Максимальный. 9. Псевдомедианный. Блок статистического анализа позволяет произвести обработку набора изображений с различными плотностями вероятности распределения яркости с заданной величиной выборки каждого изображения из набора. Библиотека алгоритмов оптимизации, связанная с блоком оптимизации, что отражено на рисунке 3.2, взаимодействует с блоками пространственной и временной фильтрации. Библиотека алгоритмов оптимизации содержит методы локальной и глобальной оптимизации. В качестве локальных методов выступают следующие методы многомерной оптимизации: 10.Метод Ньютона. 11.Квазиньютоновский метод с DFP-формулой пересчета. 12.Квазиньютоновский метод с преобразованной BFGS-формулой. 13.Метод сопряженных градиентов. В качестве метода глобальной оптимизации используется метод динамического программирования (ДП). В библиотеке алгоритмов оптимизации представлено три метода ДП: 14.Классический метод ДП. 15.Модифицированный метод ДП. 16.ДП со случайной сеткой. Таким образом, в блоке фильтрации изображений происходит формирование целевой функции, находится ее минимум и соответствующий этому минимуму оптимальный вектор весовых коэффициентов 4.
Исследование обработки реальных изображений с различными статистическими характеристиками проводится с использованием программного комплекса Space-time image processing 32 (STIP32), структура модели которого рассмотрена в предыдущем разделе. Программа пространственно-временной обработки изображений разработана на языке Си и имеет удобный графический интерфейс пользователя. Табличный ввод данных, система окон и меню обеспечивают быстрое освоение программы, не требующее специальной подготовки. В программе реализован контроль информации, вводимой пользователем, при некорректных данных ему обеспечивается соответствующая подсказка. Вводимая информация, результаты фильтрации, а также весовые коэффициенты могут быть сохранены. Использование языка Си и Ассемблера при разработке математического ядра и интерфейса приводит к уменьшению размера исполняемого модуля и увеличению производительности базовых алгоритмов. Кроме этого, исследование влияния оптимизирующих свойств современных Си-компиляторов на производительность вычислительных программ показало, что наиболее компактный и производительный код генерирует компилятор Watcom C++ 10.0, который и был использован для создания данной программы. Программный комплекс работает на компьютерах типа IBM PC с VGA адаптером под управлением MS-DOS версии 3.30 и выше, занимает около 80K пространства на жестком диске. После запуска программы на экране появляется рабочее окно программы. Окно содержит основные элементы интерфейса, отвечающие за ввод и вывод информации. Элементами ввода / вывода информации являются: 1. Раскрывающийся список, позволяющий сделать выбор фильтра, используемого при выделении ТВ сигнала на фоне помех и шумов. 2. Выбор типа фильтрации: . Загрузка обрабатываемого изображения. При нажатии на кнопку [F3] «Загрузить» появляется диалоговое окно «Обзор», в котором пользователю предоставляется возможность выбора тестового изображения в формате *.pcx. 4. Выбор параметров параметрической оптимизации. При вводе параметров оптимизации вызывается диалоговое окно «Параметры оптимизации». Для задания параметров оптимизации пользователю необходимо: 1) Выбрать в выпадающем списке метод первого (глобального) этапа. 2) Выбрать в выпадающем списке метод второго (локального) этапа. ) Выбрать в выпадающем списке вид барьерной функции. ) Задать параметры локальных методов оптимизации: – относительное приращение аргумента; · штрафной коэффициент; · пороговую точность адаптации; · относительное приращение градиента; · нижнюю границу весовых коэффициентов; · верхнюю границу весовых коэффициентов. 5) Задать параметры глобальных методов оптимизации: – количество итераций; – число точек на интервале. 6) Заполнить таблицу признаков оптимизации по следующему правилу: если признак оптимизации равен 0, то соответствующий весовой коэффициент не будет изменяться в ходе оптимизации, в противном случае (признак оптимизации не равен 0) - будет. 5. Редактирование и просмотр весовых коэффициентов для обработки изображений. При нажатии клавиши F4 (кнопка «Веса»), у пользователя появляется возможность, в раскрывшемся окне «Весовые коэффициенты», редактировать или просмотреть весовые коэффициенты. 6. Загрузка ранее полученных весовых коэффициентов. Нажатие клавиши F5 (кнопка «Загрузить веса») приводит к открытию окна «Открыть» в котором можно указать путь к ранее сохраненным весовым коэффициентам, записанным в файле с расширением *.txt, и открыть этот файл. Указание пути к файлу с весовыми коэффициентами осуществляется посредством окон «Папки» и «Диски», все найденные по указанному пути файлы с расширением *.txt будут отображены в окне «Файлы». Для выбора необходимого файла, потребуется навести на его имя, в окне «Файлы», курсор и нажать правую кнопку мыши, чтобы его подсветить, затем нажать OK. 7. Запуск процесса параметрической оптимизации. При условии заданных ранее параметрах оптимизации, нажатие клавиши F9 (кнопка «Оптимизация») приводит к запуску процесса оптимизации. 8. Сохранение новых весовых коэффициентов. В случае необходимости сохранения, полученных весовых коэффициентов, нажатие клавиши F2 (кнопка «Сохранить веса») приводит к открытию окна «Сохранить как». Для сохранения коэффициентов в файле с расширением *.txt, необходимо ввести имя файла в графу «Имя файла» и указать путь сохранения, используя для этого окна «Папки» и «Диски». После этого нажать кнопку OK. 9. Установка параметров статистического анализа. Нажатие клавиши F8 (кнопка «Параметры стат. анализа») активирует окно «Параметры статистического анализа». В данном окне производятся выбор серии изображений, по которым будет проводиться исследование, и установка величины выборки каждого изображения в процессе статистического анализа. Помимо этого, установка галочки у опции «Оптимизация», позволяет произвести оптимизацию весовых коэффициентов по всему заданному набору изображений для анализа. 10. Выбор дополнительных способов обработки отфильтрованного ТВ изображения. Нажатием клавиши F7 (кнопка «Доп. обработка»), открывается окно «Дополнительная обработка отфильтрованного изображения». Выбор требуемого вида обработки производится с путем установки точки, слева от названия вида обработки. 11. Запуск статистического анализа. Если предварительно были заданы параметры статистического анализа, то нажатие комбинации клавиш Ctrl+F9 (кнопка «Стат. анализ») запускает процесс статистического анализа, информация о ходе которого отображается в окне «Информация о ходе статистического анализа». 12. Установка размера апертуры фильтра. Размер апертуры устанавливается в пределах от 2 до 15. 13. Ввод значения вероятности появления белого Возможные значения лежат в пределах от 0 до 0.5. 14. Ввод значения вероятности появления черного . Ввод значения СКО белого шума . Установка значения параметра Q для контргармонического фильтра. . Индикаторы статистических характеристик: 1) СКО1 - СКО зашумленного изображения; 2) СКО2 - СКО отфильтрованного изображения; 3)
4) ПОСШ1 - пиковое отношение сигнал-шум на входе фильтра (дБ); 5) ПОСШ2 - пиковое отношение сигнал-шум на выходе фильтра (дБ):
6) Pч1 - вероятность появления черного импульсного шума на зашумленном изображении; 7) Pч2 - вероятность появления черного импульсного шума на отфильтрованном изображении (вероятность ложного воспроизведения); 8) Pб1 - вероятность появления белого импульсного шума на зашумленном изображении; 9) Pб2 - вероятность появления белого импульсного шума на отфильтрованном изображении (вероятность ложного воспроизведения); 10) Кп ср - средний коэффициент улучшения СКО на выходе фильтра, рассчитанный путем статистического усреднения по набору тестовых изображений (дБ); 11) ПОСШ1ср - среднее значение ПОСШ на входе фильтра, рассчитанное путем статистического усреднения по набору тестовых изображений (дБ); 12) ПОСШ2ср - среднее значение ПОСШ на выходе фильтра, рассчитанное путем статистического усреднения по набору тестовых изображений (дБ). 18. Аппроксимированные плотности вероятности распределения яркости исходного не зашумленного изображения и отфильтрованного. Таким образом, для выполнения весовой пространственной или временной фильтрации, пользователю необходимо выполнить следующие действия: 1) Выбрать в главном окне программы нужное изображение. Если же требуется произвести статистический анализ, то установить параметры статистического анализа (F8); 2) Выбрать требуемый вид фильтра; ) Выбрать необходимый вид фильтрации; ) Установить требуемый размер апертуры, требуемые значения СКО белого шума и вероятностей импульсного шума; ) Выбрать метод 1-го (глобального) этапа (нет, ДП классический, ДП модифицированный или ДП со случайной сеткой); ) Выбрать метод 2-го (локального) этапа (Ньютона, DFP, преобразованный BFGS или метод сопряженных градиентов); ) Выбрать вид барьерной функции (логарифмическая или обратная); ) Установить параметры глобальных и локальных методов и указать признаки; ) Запустить оптимизацию, нажав кнопку «Оптимизация» (клавишу F9). ) После этого результаты выполнения программы можно посмотреть на дисплее и при необходимости запустить оптимизацию повторно с другими параметрами. 5.
В экспериментальной части дипломного проекта разработаны методика проведения и порядок выполнения лабораторной работы №1 «Исследование эффективности пространственно-временной обработки изображений с использованием статистик среднего ранга при наличии импульсных помех».
Расчет ленточного графика
При проведении проектных работ для их реализации и рациональной организации при ограничении на сроки разработки необходимо предварительно спланировать проектные мероприятия. Целесообразно определить перечень проектных работ, трудоемкость каждой из них и привести в соответствие общую продолжительность проведения проектных мероприятий со сроками, отпущенными на разработку[27]. Принцип построения ленточного графика осуществляется в следующем порядке: 1. Определяются этапы и состав работ по подготовке производства, технической документации с установлением количества чертежей каждого формата. 2. Для каждого этапа разработки производства устанавливается число исполнителей и продолжительность. . Определяется трудоемкость выполнения каждого этапа. Продолжительность каждой работы Тп будет определяться по формуле:
где Ti - трудоемкость работ, человеко-дни, ni - численность исполнителей, человек. Перечень проводимых работ указан в таблице 6.1. Там же приводятся исполнители и продолжительность выполнения работ.
Таблица 6.1 - Данные для построения ленточного графика
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-03-13; просмотров: 473; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.01 с.) |

 , полученных в дискретные моменты времени (рисунок 2.2). Апертура
, полученных в дискретные моменты времени (рисунок 2.2). Апертура  , в этом случае, принимает временной характер, то есть включает в себя соответственные пиксели всех
, в этом случае, принимает временной характер, то есть включает в себя соответственные пиксели всех  кадров (заштрихованные пиксели на рисунке 2.2).
кадров (заштрихованные пиксели на рисунке 2.2).
 передвигается от пикселя к пикселю, начиная с верхнего левого угла, при этом в каждой точке
передвигается от пикселя к пикселю, начиная с верхнего левого угла, при этом в каждой точке  выполняется оператор фильтрации
выполняется оператор фильтрации  , давая отклик фильтра:
, давая отклик фильтра: .
. ;
; ;
; ;
; ;
; ;
; ;
; ;
; .
. ,
, - весовая функция, которая вместе с апертурой
- весовая функция, которая вместе с апертурой  формирует маску.
формирует маску.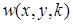 поэлементно умножается на значения соответствующих пикселей кадров
поэлементно умножается на значения соответствующих пикселей кадров 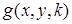 ,
,  . Полученные произведения подвергаются затем действию оператора фильтрации
. Полученные произведения подвергаются затем действию оператора фильтрации  , который и определяет отклик фильтра
, который и определяет отклик фильтра  для данной точки. При этом весовая функция в процессе перемещения маски остается неизменной.
для данной точки. При этом весовая функция в процессе перемещения маски остается неизменной.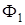 на W и полагается
на W и полагается  .
.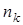 распределение
распределение  , при этом получаются точки
, при этом получаются точки  . В этих точках вычисляются значения функции
. В этих точках вычисляются значения функции  и полагается
и полагается 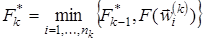 . В качестве приближения к точке
. В качестве приближения к точке  выбирается такая точка
выбирается такая точка  , в которой
, в которой  .
. на W.
на W.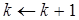 .
. . Указанные ограничения можно записать в общем виде:
. Указанные ограничения можно записать в общем виде: ,
,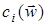 - непрерывно дифференцируемая функция. При этом произвольная точка
- непрерывно дифференцируемая функция. При этом произвольная точка  .
. ,
, - вектор управляющих параметров,
- вектор управляющих параметров,  - «штрафная» функция, воздействие которой регулируется вектором
- «штрафная» функция, воздействие которой регулируется вектором 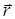 , а
, а  . Различные методы преобразования отличаются друг от друга выбором
. Различные методы преобразования отличаются друг от друга выбором  и способом задания управлений, позволяющим найти минимум функции
и способом задания управлений, позволяющим найти минимум функции  при наличии ограничений посредством безусловной минимизации
при наличии ограничений посредством безусловной минимизации  по
по  . Если обозначить точку безусловного локального минимума функции
. Если обозначить точку безусловного локального минимума функции  через
через  , то методы преобразования, в которых функция
, то методы преобразования, в которых функция  и последовательность
и последовательность  задаются так, что точки
задаются так, что точки  при
при  , называются методами последовательной безусловной минимизации или просто последовательными методами [17]. Последовательные методы распадаются на два класса. Первый - это методы штрафных функций (или, как они еще называются методами внешней точки), использующие при поиске недопустимые точки. Второй класс составляют методы барьерных функций (методы внутренней точки). Они характеризуются тем, что поиск решения осуществляется, не выходя за пределы допустимой области, что является определяющим при решении задач нелинейной регрессии, для которых целевая функция
, называются методами последовательной безусловной минимизации или просто последовательными методами [17]. Последовательные методы распадаются на два класса. Первый - это методы штрафных функций (или, как они еще называются методами внешней точки), использующие при поиске недопустимые точки. Второй класс составляют методы барьерных функций (методы внутренней точки). Они характеризуются тем, что поиск решения осуществляется, не выходя за пределы допустимой области, что является определяющим при решении задач нелинейной регрессии, для которых целевая функция  вне W может быть не определена. Поэтому целесообразно рассмотреть только методы барьерных функций.
вне W может быть не определена. Поэтому целесообразно рассмотреть только методы барьерных функций. подбирается так, чтобы на границе допустимой области «построить барьер», препятствующий нарушению ограничений в процессе безусловной минимизации функции
подбирается так, чтобы на границе допустимой области «построить барьер», препятствующий нарушению ограничений в процессе безусловной минимизации функции  , и чтобы точки
, и чтобы точки 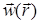 с изменением
с изменением 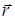 по некоторому правилу приближались к
по некоторому правилу приближались к 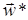 изнутри W. При этом барьерная функция определяется выражением [17]:
изнутри W. При этом барьерная функция определяется выражением [17]: ,
, - непрерывные на интервале
- непрерывные на интервале  дифференцируемые функции, причем
дифференцируемые функции, причем  при
при 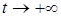 . Вспомогательная функция имеет вид:
. Вспомогательная функция имеет вид: .
. для какого-нибудь i. Наиболее часто используются следующие барьерные функции [11,17]:
для какого-нибудь i. Наиболее часто используются следующие барьерные функции [11,17]: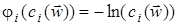 ;
;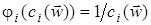 .
. . Это обеспечивает сходимость при
. Это обеспечивает сходимость при 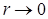 точек
точек  к
к  и как следствие существенное убывание значения
и как следствие существенное убывание значения  и совпадение его в пределе с
и совпадение его в пределе с 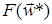 .
.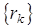 , например,
, например,  . Определяется начальное приближение
. Определяется начальное приближение  и полагается
и полагается  .
. .
. , находится безусловный локальный минимум для
, находится безусловный локальный минимум для  и принимается
и принимается  . Если критерий остановки не выполняется, то возвращаются к шагу 2.
. Если критерий остановки не выполняется, то возвращаются к шагу 2. сходится к
сходится к  при условии непрерывности функции
при условии непрерывности функции  встречает определенные трудности [17]. Так стандартные методы безусловной минимизации рассчитаны на то, что целевая функция определена на всем пространстве. Но для функции
встречает определенные трудности [17]. Так стандартные методы безусловной минимизации рассчитаны на то, что целевая функция определена на всем пространстве. Но для функции  это условие не выполняется, и, чем ближе
это условие не выполняется, и, чем ближе  к границе множества W, тем реальнее возможность сделать шаг за пределы допустимой области. Следовательно, в данном случае необходима специальная процедура спуска по направлению, включающая проверку соблюдения ограничений и эффективное правило сокращения недопустимого шага. Вполне эффективным является следующий метод [17]. Если имеются точка
к границе множества W, тем реальнее возможность сделать шаг за пределы допустимой области. Следовательно, в данном случае необходима специальная процедура спуска по направлению, включающая проверку соблюдения ограничений и эффективное правило сокращения недопустимого шага. Вполне эффективным является следующий метод [17]. Если имеются точка  , направление поиска метода
, направление поиска метода  и необходима следующая точка
и необходима следующая точка  , то сначала выбирается значение шага
, то сначала выбирается значение шага  , проверяется выполнение ограничений
, проверяется выполнение ограничений 
 . Если они выполняются, то
. Если они выполняются, то  не меняется, иначе
не меняется, иначе  заменяется величиной
заменяется величиной  (где
(где  - коэффициент коррекции шага), находится новая точка
- коэффициент коррекции шага), находится новая точка  и вновь осуществляется проверка. В конце концов, допустимая точка
и вновь осуществляется проверка. В конце концов, допустимая точка 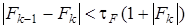 ,
, .
. и
и  к своим пределам. Параметр
к своим пределам. Параметр  определяет число правильных разрядов
определяет число правильных разрядов  , которое хотелось бы получить. Например, выбор
, которое хотелось бы получить. Например, выбор  означает, что при
означает, что при  желательно, чтобы у
желательно, чтобы у  и
и  совпадали пять первых значащих цифр, а при
совпадали пять первых значащих цифр, а при  , чтобы
, чтобы  и
и  различались бы не более чем на
различались бы не более чем на  .
.
 и
и 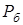 появления импульсного шума, выбирает вид целевой функции, метод оптимизации), используя интуитивно понятный графический интерфейс. Эти данные поступают в блок фильтрации изображений и блок оптимизации.
появления импульсного шума, выбирает вид целевой функции, метод оптимизации), используя интуитивно понятный графический интерфейс. Эти данные поступают в блок фильтрации изображений и блок оптимизации.
 .
.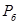 импульсного шума.
импульсного шума.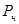 импульсного шума. Также как и для белого импульсного шума, вероятность черного импульсного шума можно задать в пределах от 0 до 0.5.
импульсного шума. Также как и для белого импульсного шума, вероятность черного импульсного шума можно задать в пределах от 0 до 0.5. .
. - коэффициент улучшения СКО на выходе фильтра (дБ):
- коэффициент улучшения СКО на выходе фильтра (дБ): ;
; ;
; ,
,


