
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классификация методов локальной оптимизацииСодержание книги
Поиск на нашем сайте
Методы поиска локального экстремума принято ранжировать следующим образом [12-18]: 1. Метод Ньютона и его модификации. 2. Квазиньютоновские методы. . Градиентные методы. . Методы прямого поиска. Согласно этой классификации первенство держат ньютоновские методы, поскольку использование информации второго порядка обеспечивает им высокие скорости сходимости и позволяет делать качественные выводы относительно найденного численного решения. Когда получение аналитических выражений первых и вторых производных затруднено, лучшим будет использование квазиньютоновских методов с конечно-разностной аппроксимацией производных. Градиентные методы значительно уступают по своей эффективности ньютоновским и квазиньютоновским вследствие низких скоростей сходимости, но наиболее широко используются из-за простоты реализации. Методы прямого поиска при минимизации используют только значения целевой функции, поэтому они гораздо менее эффективны, чем градиентные, в тех случаях, когда последние применимы. Таким образом, чем больше информации о производных, которую можно получить ценой приемлемых затрат, будет использовано при решении задачи, тем лучше. Большинство методов минимизации являются итерационными по своей природе. Это означает, что, начиная с заданной точки
где Так, в методе Ньютона направление поиска определяется системой линейных алгебраических уравнений:
где Необходимо заметить, что численное определение матрицы Гессе на каждой итерации существенно снижает скорость сходимости (из-за наличия ошибок округления), а также значительно увеличивает объем вычислительных затрат.
В квазиньютоновских методах направление поиска
где
где 1. Симметричная формула ранга один (SR1-формула):
где 2. Формула Бройдена-Флетчера-Гольдфарба-Шанно (BFGS-формула):
где 3. Формула Дэвидона-Флетчера-Пауэлла (DFP-формула):
В последнее время в литературе, посвященной квазиньютоновским методам, был предложен ряд алгоритмов, использующих иную схему безусловной минимизации [14, 18]. Она отличается от классической квазиньютоновской схемы тем, что предполагает непосредственную оценку
которое решается с использованием разложения матрицы по методу Холесского Каждой квазиньютоновской формуле для пересчета оценки обратной матрицы Гессе 4. Преобразованная симметричная формула ранга один (SR1-формула):
где
5. Преобразованная BFGS-формула:
6. Преобразованная DFP-формула:
где
Следует отметить, что преобразованные формулы не содержат операции умножения матрицы на вектор. Имея разложение Холесского матриц Помимо этого, использование факторизации Холесского позволяет избежать потери положительной определенности матриц
Используя в квазиньютоновском поиске факторизацию Холесского, легко обеспечить положительную определенность матрицы
где Методы сопряженных градиентов относятся к классу алгоритмов минимизации, в которых вычисление направлений поиска не предполагает решения каких-либо систем линейных уравнений. Это принципиально отличает их от методов Ньютона и квазиньютоновских методов [12, 14]. ожно показать [12, 14], что направление
где
Формула Флетчера-Ривса: Формула Полака-Рибьера:
Теоретически этот метод конечен [12]: при точных вычислениях он должен найти решение не более чем за n шагов. Метод сопряженных градиентов легко обобщается на задачи минимизации нелинейных функций общего вида. Для этого надо заменить используемую в нем формулу расчета Традиционный метод сопряженных градиентов сходится в тех же предположениях, что и метод наискорейшего спуска [11,15]. Для достаточно широкого класса функций теоретическая скорость его сходимости при точной одномерной минимизации оказывается n -шаговой сверхлинейной. Однако, как показывает практический опыт, из-за ошибок округления реальная скорость сходимости метода сопряженных градиентов почти всегда линейна независимо от того, применяются рестарты или нет [11]. Поэтому применение метода сопряженных градиентов следует считать успешным, когда удовлетворительное решение удалось получить менее чем за 5 n шагов.
В заключение следует отметить, что, хотя схема сопряженных градиентов далека от идеала, на сегодня она является единственным разумным универсальным средством решения задач безусловной минимизации с очень большим числом переменных.
|
|||||||
|
Последнее изменение этой страницы: 2020-03-13; просмотров: 208; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.178.145 (0.007 с.) |

 , называемой начальным приближением, в дальнейшем получается последовательность точек
, называемой начальным приближением, в дальнейшем получается последовательность точек  , которая, в принципе, должна сходится к точке
, которая, в принципе, должна сходится к точке  минимума целевой функции
минимума целевой функции  . Вычисление
. Вычисление  называется k -й итерацией, а точка
называется k -й итерацией, а точка  - k -м приближением. В результате основное уравнение для k -й итерации записывается в виде:
- k -м приближением. В результате основное уравнение для k -й итерации записывается в виде: ,
,  ,
, - скалярная величина (длина шага), обеспечивающая неравенство
- скалярная величина (длина шага), обеспечивающая неравенство  ,
,  - направление поиска, правила вычисления которого «определяют лицо алгоритма» минимизации и его эффективность.
- направление поиска, правила вычисления которого «определяют лицо алгоритма» минимизации и его эффективность. ,
, - матрица Гессе, матрица вторых частных производных, а
- матрица Гессе, матрица вторых частных производных, а  - вектор градиента функции
- вектор градиента функции  .
.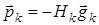 ,
,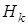 - приближение обратной матрицы Гессе. Матрица
- приближение обратной матрицы Гессе. Матрица  на первой итерации является единичной и преобразуется от итерации к итерации в соответствии со следующей формулой пересчета:
на первой итерации является единичной и преобразуется от итерации к итерации в соответствии со следующей формулой пересчета: ,
, - поправочная матрица различных рангов. Существуют различные формулы пересчета приближений обращенной матрицы Гессе, использующие поправки разных рангов [14, 17]:
- поправочная матрица различных рангов. Существуют различные формулы пересчета приближений обращенной матрицы Гессе, использующие поправки разных рангов [14, 17]: ,
, , а
, а  - соответствующее приращение градиента.
- соответствующее приращение градиента. ,
, .
. .
. прямой матрицы Гессе
прямой матрицы Гессе  , а не обратной к ней. В этом случае направление спуска определяется из уравнения:
, а не обратной к ней. В этом случае направление спуска определяется из уравнения: ,
, .
. , соответствует (в том смысле, что из
, соответствует (в том смысле, что из  следует
следует  , где
, где 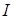 - единичная матрица) преобразованная формула пересчета матрицы
- единичная матрица) преобразованная формула пересчета матрицы  [14, 15, 18]:
[14, 15, 18]: ,
, .
. .
. ,
, .
. , где
, где  - максимальный и минимальный диагональные элементы фактора
- максимальный и минимальный диагональные элементы фактора  . На промежуточных операциях такие оценки позволяют выявить ситуации, когда матрица
. На промежуточных операциях такие оценки позволяют выявить ситуации, когда матрица  обусловлена так плохо, что вычисляемый вектор
обусловлена так плохо, что вычисляемый вектор  из-за ошибок округления не будет направлением спуска. При этом факторы разложения можно подправить так, что обусловленность реализующей матрицы станет приемлемой [14, 15].
из-за ошибок округления не будет направлением спуска. При этом факторы разложения можно подправить так, что обусловленность реализующей матрицы станет приемлемой [14, 15]. (
( может указывать в сторону возрастания минимизируемой функции. При этом по данным функционирования обычного (без факторизации) квазиньютоновского алгоритма невозможно определить момент утраты положительной определенности
может указывать в сторону возрастания минимизируемой функции. При этом по данным функционирования обычного (без факторизации) квазиньютоновского алгоритма невозможно определить момент утраты положительной определенности  увеличивается настолько, чтобы окончательное произведение
увеличивается настолько, чтобы окончательное произведение  было положительно определенным и хорошо обусловленным. Когда этот элемент выбран, очередной столбец множителя
было положительно определенным и хорошо обусловленным. Когда этот элемент выбран, очередной столбец множителя  однозначно определяется требованием совпадения матриц
однозначно определяется требованием совпадения матриц  и
и  . Таким образом, в результате получается представление:
. Таким образом, в результате получается представление: ,
, - неотрицательная диагональная матрица, равная нулю, если матрица
- неотрицательная диагональная матрица, равная нулю, если матрица  существенно положительно определена.
существенно положительно определена. для очередной итерации в методе сопряженных градиентов при минимизации квадратичных функций вычисляется как линейная комбинация градиента в текущей точке
для очередной итерации в методе сопряженных градиентов при минимизации квадратичных функций вычисляется как линейная комбинация градиента в текущей точке  и предыдущего направления
и предыдущего направления  :
: ,
, вычисляются по следующим теоретически эквивалентным формулам [12]:
вычисляются по следующим теоретически эквивалентным формулам [12]: .
. .
. какой-нибудь процедурой одномерного поиска и уточнить, будет ли направление
какой-нибудь процедурой одномерного поиска и уточнить, будет ли направление  всегда вычисляться по формуле (2.2-17) или допускаются периодические отступления. Последние принято называть рестартамиили восстановлениями [11, 14]. Можно, например, принимая во внимание n -шаговую теоретическую сходимость в квадратичном случае, через каждые n шагов отказываться от направления (15) и брать в качестве очередного
всегда вычисляться по формуле (2.2-17) или допускаются периодические отступления. Последние принято называть рестартамиили восстановлениями [11, 14]. Можно, например, принимая во внимание n -шаговую теоретическую сходимость в квадратичном случае, через каждые n шагов отказываться от направления (15) и брать в качестве очередного  антиградиент
антиградиент  . Соответствующий метод называют традиционным [11].
. Соответствующий метод называют традиционным [11].


