
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Двухэтапный алгоритм весовой фильтрацииСодержание книги
Поиск на нашем сайте
Трудность разработки и применения наиболее эффективных методов минимизации при весовой фильтрации обусловлена невозможностью оценить свойства минимизируемой функции. Как правило, минимизируемая функция является многоэкстремальной, что создает трудности в применении методов локального спуска, так как это требует знания хорошего начального приближения, тяготеющего к достаточно глубокому локальному (в наилучшем варианте - глобальному) минимуму. Поэтому поиск хороших начальных приближений для методов локального спуска в задачах весовой фильтрации является важной самостоятельной проблемой, от решения которой зависит окончательный результат. Другая трудность решения задачи (2.2-2) связана с учетом ограничений на вектор Необходимо отметить еще одну трудность, сопутствующую задаче вида (2.2-2). Имеется в виду разнородность компонент вектора весовых коэффициентов. Это может привести к появлению многомерных «оврагов» у целевой функции, что препятствует высокой скорости сходимости методов спуска при оптимизации в совокупном пространстве В связи с особенностями целевой функции (многоэкстремальность, не выпуклость, неаналитичность, плохая обусловленность) при решении задачи (2.2-2) необходимо использовать алгоритм, состоящий из двух этапов - глобального и локального [19,20]. На первом этапе с использованием одного из методов глобальной оптимизации находится грубое приближение оптимального вектора весовых коэффициентов Глобальный случайный поиск Исторически первым и довольно долгое время единственным широко используемым методом поиска глобального экстремума являлся метод, названный впоследствии «мультистарт». Этот метод состоит в многократном (последовательном или параллельном) отыскании локальных минимумов из различных начальных точек, чаще всего случайных (такой вид алгоритма носит название «случайный мультистарт») [8]. Использование случайного выбора при построении алгоритмов глобальной оптимизации приводит к алгоритмам глобального случайного поиска [17]. Основными причинами популярности методов случайного поиска среди пользователей являются следующие. Структура алгоритмов довольно проста, и их можно легко реализовать в виде программ ЭВМ. Алгоритмы робастны, то есть малочувствительны к нерегулярностям поведения целевой функции, структуры множества оптимизации, наличию случайных ошибок при вычислении функции; кроме того, они малочувствительны к росту размерности множества оптимизации. Наконец, в рамках известных схем случайного поиска легко строятся новые алгоритмы, реализующие различные эвристические процедуры адаптации. Разработано большое разнообразие методов глобального случайного поиска [17]. В основе построение этих алгоритмов лежит следующая общая схема: Выбирается некоторое распределение вероятностей Моделируется некоторое число раз Согласно определенному правилу конструируется распределение вероятностей Проверяется условие останова, и если оно не выполняется, то осуществляется переход к шагу 2 с заменой Таким образом, любой алгоритм глобального случайного поиска состоит из некоторого числа итераций, на каждой из которых моделируется специальным образом сконструированные распределения. К сожалению, для алгоритмов глобального случайного поиска нет повода испытывать оптимизм. Причины для этого следующие [17]. Во-первых, хотя большинство методов обладает теоретическим свойством сходимости, оценки этой скорости сходимости показывают, что она крайне медленная. Во-вторых, методы случайного поиска, обладающие наибольшей практической эффективностью, содержат в себе элементы эвристики и поэтому обладают недостатком, присущим эвристическим методам: нечетко определен класс задач, для которых методы эффективны; отсутствуют четкие рекомендации о выборе параметров методов, а эти параметры в значительной степени влияют на эффективность. В-третьих, как показывают численные и теоретические результаты, только за счет усложнения алгоритма и уменьшения доли случайности можно повысить его эффективность. Следовательно, применение алгоритмов глобального случайного поиска при решении задачи весовой фильтрации наиболее рационально для минимизации функций, вычисление которых не требует значительных затрат машинного времени.
|
||||
|
Последнее изменение этой страницы: 2020-03-13; просмотров: 206; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.22.34 (0.01 с.) |

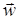 . В регулярных методах спуска, особенно основанных на градиентной информации, наличие ограничений изменяет либо схему метода, либо минимизируемую функцию (метод штрафных функций), вводя в него информацию о расстоянии текущей точки спуска до границы допустимой области. И в том, и в другом случае схема оптимизации значительно усложняется [5].
. В регулярных методах спуска, особенно основанных на градиентной информации, наличие ограничений изменяет либо схему метода, либо минимизируемую функцию (метод штрафных функций), вводя в него информацию о расстоянии текущей точки спуска до границы допустимой области. И в том, и в другом случае схема оптимизации значительно усложняется [5]. . Сходимость процесса повышается при циклическом переборе спусков в пространстве однородных весовых коэффициентов.
. Сходимость процесса повышается при циклическом переборе спусков в пространстве однородных весовых коэффициентов.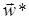 (область глобального экстремума). А на втором этапе компоненты вектора
(область глобального экстремума). А на втором этапе компоненты вектора 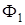 на W и полагается
на W и полагается  .
.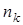 распределение
распределение  , при этом получаются точки
, при этом получаются точки  . В этих точках вычисляются значения функции
. В этих точках вычисляются значения функции  и полагается
и полагается 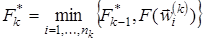 . В качестве приближения к точке
. В качестве приближения к точке  выбирается такая точка
выбирается такая точка  , в которой
, в которой  .
. на W.
на W.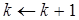 .
.


