
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общие сведения о методах оптимизацииСодержание книги
Поиск на нашем сайте
Алгоритмы оптимального управления (АОУ), использованные в АИУС, разрабатываются на базе различных математических методов. Наиболее распространённые среди них: 1. Методы линейного программирования. 2. Градиентные методы оптимизации. 3. Методы покоординатного спуска. 4. Методы динамического программирования. 5. Методы нелинейного программирования и т.д. Выбор метода оптимизации наиболее подходящего для функций (задач) данной конкретной АИУС определяется спецификой (или особенностью) объекта и его модели, спецификой выбранного критерия эффективности, а также,— возможностями аппаратных и программных средств. Чтобы решить задачу оптимального управления в АИУС создается операционная математическая модель, режима объекта. В частности при оптимизации в установившемся режиме ОММ имеет вид:
ОММ: 1. Математическая модель 2. Критерий эффективности (КЭ) 3. ограничения: Постановка задачи: необходимо найти такой вектор входных или управляющих воздействий обеспечивается выполнение ограничений; значение критерий эффективности достигает экстремума: W=Wextr=W( В зависимости от конкретных видов функциональных связей в соотношениях 1,2,3 применяются различные методы оптимизации, в том числе и перечисленные выше. В частности, если 1,2,3 – линейны, то могут быть применены методы линейного программирования, а сама ОММ называется ЛОММ. Рассмотрим на примере как строиться линейная операционная модель и реализацию метода поиска оптимума. 4.6.2 Построение линейной операционной модели для решения задач оперативного планирования производства
В качестве объекта, для которого будет строиться операционная линейная математическая модель, рассмотрим объект (производство), для которого известно следующее: 1. на нем перерабатывается различные виды сырья i-го вида Si, (i=1,…m). 2. в результате переработки изготавливаются различные виды продукции j-го вида- Pj, (j=1,…n). 3. запасы каждого вида сырья Si ограничены и равны bi. 4. на производство единицы продукции j-го вида (Pj) расходуется aij единиц сырья Si. 5. при реализации единицы продукции j-го вида (Pj) получается прибыль Cj. Необходимо так спланировать работу данного производства на заданный отрезок времени (месяц, неделю), чтобы при заданных ограничениях по сырью была получена максимальная прибыль для данного производства. Отразим всё вышесказанное об объекте в виде таблицы:
Введем обозначения: Х1,…,Хj,…,Xn, где Xj – количество единиц продукции Pj, запланированное для производства на данном объекте, на заданный период (смену, сутки, месяц и т.д.). В таком случае, можно сформировать выражение для оценки прибыли производства W за выбранный период, получаемый от реализации готовой продукции:
W — общая прибыль. А так же, кроме того можно выразить аналитически расходы сырья и ограничения на величины Х1,…,Хj,…,Хn, обусловленные заданными ограниченными объемами сырья:
В системе ограничений (2) Кроме того, нужно записать ограничения в виде (3) Поскольку соотношения (1), (2), (3) являются линейными относительно искомых переменных X1,…,Xn, то это пример линейной операционной математической модели. А постановка задачи поиска оптимального плана в математическом виде формируется следующим образом: необходимо найти такие неотрицательные значения X1,…,Xn, которые удовлетворяют системе ограничений (2) и обеспечивают максимум линейной функции W в соотношении (1). Для того чтобы можно было применить уже разработанные ранее методы поиска оптимального решения, исходную постановку данной задачи (которая называется задачей линейного программирования) приводят к так называемой канонической форме, при которой:
1. Критерий эффективности должен быть устремлен к минимуму→ min. 2. Система ограничений (2) должна содержать только равенства!!! Если исходная ЗПЛ не в канонической форме, то для перехода к канонической форме постановки задачи используются следующие приёмы: Вводится новый КЭ®W¢ такого вида 1. W′= –W= Введение такой функции W′ обосновано, т.к. доказано что функция W′ достигает минимального значения при таких значениях X1,…,Xn, при которых функция W′ достигает максимального значения. 2. Если в систему ограничений (2) входят соотношения типа «неравенство» причем число их-k, то переход к канонической форме осуществляется путем введения дополнительных переменных Xn+1,…,Xn+k, причем, эти переменные вводятся по одной для каждого неравенства и со знаком «+», если неравенство типа k – общее число ограничений типа неравенств в системе ограничений (2).
Постановка задачи линейного программирования в канонической форме. Необходимо найти такие неотрицательные значения X1,… Xj…Xn,…Xn+k, которые удовлетворяют системе равенств (2) и обеспечивают минимум целевой функции W′.
Пример: Исходная постановка задачи: 1. 2. 3. Приведем к канонической форме: 1. 2. 3.
4.6.3. Сведения о решении задачи линейного программирования
Для поставленной задачи ЛП в общем виде вводим следующие обозначения: 1) W¢<C1X1….CnXn®extr 2) ……………………………….. am1x1+ …amnxn=bn 3) x1≥0, … xn≥0
Обозначим m — число уравнений, n — число неизвестных. Анализ систем (2) и (3) показывает что, может иметь место следующие случаи: 1) m=n: в этом случае решение системы уравнений (если уравнения совместимы) единственное и задача оптимизации решаться не может, т.к. область, в пределах которой может осуществляться поиск минимума или максимума критерия эффективности W обращается в точку 2) m>n: фактически соответствует предыдущему случаю. 3) m<n: в этом случае можно рассчитывать на то, что существует область, допустимых решений в рамках которой можно отыскивать экстремум, и, следовательно, такая задача может решаться как оптимизационная. Анализ системы ограничений (2) и (3) показывает, что могут иметь место следующие случаи: 1. Условия (2) и (3) противоречивы, т.е. не существует неотрицательного набора чисел Х1,…,Хn, удовлетворяющих системе (2). 2. Условия (2) и (3) непротиворечивы, но область неопределенна или не ограничена, т.е. существуют наборы чисел Х1,…,Хn которые принимают сколь угодно большие значения. 3. Условия (2) и (3) совместны, в этом случае область определена и ограничена. В последнем случае может быть найдено оптимальное решение.
ОП. 1: Допустимое решение – это всякое неотрицательное решение Х1 ОП. 2: Оптимальное решение – это одно из допустимых решений системы уравнений (2), обращающее в минимум критерий эффективности (1). Доказано в линейной алгебре, что: Если m<n, то часть переменных, число которых k=n-m, могут принимать произвольные (в определенных пределах) положительные значения. Эти переменные называются свободными (СП). Другая часть переменных, число которых m, всегда могут быть аналитически выражены через СП и такие переменные называются базисными (БП). Они не могут принимать произвольные значения, т.к. определяются исходя из системы уравнений (2), при заданных значениях свободных переменных.
В том случае, если k=2, то задачу линейного программирования можно представить (отобразить) в рамках 3-х мерного пространства, что дает возможность дать геометрическую интерпретацию и наглядно показать и понять суть метода поиска оптимального решения. Рассмотрим конкретный пример:
n=5, m=3, k=2 Поскольку выбор свободных переменных, количество которых k=2, – произвольный, то в их качестве выбираем X1 и X2. В таком случае базисные переменные: X3, X4, X5. Выразим базисные переменные через свободные переменные.
Построим в пространстве (плоскости) Х1ОХ2 т.н. допустимые полуплоскости, в которых соответствующие переменные имеют положительные (допустимые) значения. Рис. 4.6.3. График области допустимых решений.
Построив линии Х1=0 и Х2=0, перейдем к Х3=0. Для этого правую часть в (2) приравняем к 0: 6–X1–X2=0 (Х1=0 Х2=6),(Х2=0, Х1=6). Каждая из линий Х1=0,…, Х5=0 (рис 4.6.3) делит плоскость на две полуплоскости, причем одна из них называется допустимой, в которой соответствующая переменная принимает положительное значение. Геометрическое место точек в пространстве {Х1,0, Х2} которое является общим для всех допустимых полуплоскостей одновременно, называется областью допустимых решений (ОДР). Обратите внимание! В каждой из вершин плоской ОДР (в 2-хмерной плоскости) — обязательно какие-либо 2 переменные, равны нулю. Доказано, что для k³2 в общем случае ОДР представляет собой выпуклый многогранник в k–мерном пространстве. В вершине такого многогранника всегда k переменных, равных нулю. Это важный вывод и на нем базируется симплекс-метод поиск оптимального решения. Теперь продолжим построение.
Рис. 4.6.3.2. График нахождения минимума W.
Изобразим в системе координат {W,X,0,X2} ОДР и плоскость, соответствующую уравнению линейной функции W=X1+X2+2. Из рисунка можно сделать вывод, что W=Wmin в одной из вершин ОДР (Х1=0; Х2=0; Wmin=2). Этот факт не случаен, а закономерен. Т.е. доказано, что W=Wmin всегда в одной из вершин ОДР. А данная геометрическая интерпретация это лишь наглядное подтверждение, что минимум значения W достигается в одной из вершин ОДР представляющей собой выпуклый многоугольник. В общем случае, т.е. когда решение ищется в k-мерном пространстве и K>2, доказано, что W достигает минимального значения в одной из вершин выпуклого многогранника в k–мерном пространстве и в каждый из этих вершин какие-либо k переменных равны нулю. На этих выводах базируется симплекс-метод, позволяющий находить оптимальные решения задач линейного программирования. Рассмотрим суть этого алгоритма.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-03-02; просмотров: 236; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||


 ;
;
 ;
; , при котором:
, при котором: ).
). (1)
(1) (2)
(2)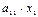 — количество сырья 1-го вида, расходуемое на производство продукции 1-го вида по плану и т.д.
— количество сырья 1-го вида, расходуемое на производство продукции 1-го вида по плану и т.д. - условие не отрицательности количества вырабатываемой продукции.
- условие не отрицательности количества вырабатываемой продукции. → min.
→ min. ; и со знаком «–» если
; и со знаком «–» если  .
.

 .
.
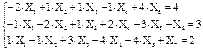
 .
.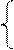 a11x1+…….a1nxn=b1
a11x1+…….a1nxn=b1









