
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проведение эксперимента . (этап 1)Содержание книги
Поиск на нашем сайте
Эксперимент, организованный в соответствии со схемой (рис.3.3.1) даёт возможность зарегистрировать и запомнить значения величины X и Y в различные моменты времени
Рис.3.3.1. Решетчатая функция. Вместо непрерывной функции X(t) имеет место ряд значений Х в различные моменты времени:
упростим запись: В результате такого эксперимента получаем набор статистических данных, которые позволяют в дальнейшем строить ММ объекта экспериментальным методом. Выбор модели. (этап 2) При проведении эксперимента с использованием описанных выше указанных аппаратных средств, непрерывные функции X и Y трансформируются в так называемые решётчатые функции (см. рис. 3.3.1), следовательно, для описания моделей объекта нельзя использовать дифференциальные уравнения, так как они предполагают непрерывность функции. При переходе от непрерывной функции к решетчатой происходит потеря части информации об объекте, но использовать решетчатые функции и разностные уравнения в качестве ММ объекта можно, если следующие условия:
т. е. количество параметров должно быть достаточно большим. В связи с этим были предложены модели в виде разностных уравнений, которые могут базироваться на решётчатых функциях. Разностное уравнение 1-го порядка имеет вид: Действительно, вспомним, что:
где В вышеприведённой формуле мы предположили, что Пример: дифференциальное уравнение 1-го порядка приемлемое для непрерывной функции:
Разностное уравнение получается путём подстановки вместо дифференциала
C(Yi-Yi-1)+KiYi-1=K2Xi-1, C – константа.
Аналогично можно показать соответствие ДУ 2-го порядка и РУ 2-го порядка и т. д. РУ N-го прядка имеет вид Группировка данных. (этап 3) На этом этапе формируются данные в соответствии со следующей таблицей удобной для определения соответствующих
Из таблицы видно, что по формулам и экспериментальным данным для каждого момента времени ti можно определить Вычисление коэффициентов А0 и В0. (этап 4) Для определения А0 и В0 разностного уравнения
Для нахождения таких значений А0 и В0 при которых L® min необходимо сформировать частные производные L и приравнять их к нулю.
или
упрощая запись, получаем:
Из полученной системы алгебраических уравнений с двумя неизвестными можем определить значения А0 и В0. Представим данную систему уравнений в матричной форме:
Из этой системы можно найти значения А0 и В0:
Определитель:
Получаем минор A0 путём замены 1-го столбца квадратной матрицы на матрицу-столбец правой части:
минор A0=
минор Bo=
Проверка полученной математической модели на адекватность (этап 5) Для реализации этого этапа используются 2 подхода. Оба вычисляют среднеквадратичную ошибку (среднеквадратичное отклонение, СКО) S:
1) В 1-ом подходе S1 сравнивается с Sдоп. Если S1≤Sдоп(Δ), то модель считается адекватной; 2) 2-й подход. При нём сравниваются S моделей разного порядка S1 и S2. Если Выбор модели объекта в виде разностного уравнения более высокого порядка. (Этап 6) Разностное уравнение 2-го порядка имеет вид:
Начнём заново рассматривать алгоритм, начиная с пункта 3.3.3.
Этап 3
Этап 4
Получим:
После некоторых преобразований получаем систему 4-х уравнений с 4-мя неизвестными А0, А1, В0, В1:
Представляем эту систему уравнений в матричной форме:
Для определения А0, А1, В0, В1 находим миноры:
и аналогично для миноров по А1, В0, В1. Используя полученное выражение, запишем формулы для определения А0 и В0, А1 и В1.
Этап 5 Для оценки адекватности ММ вычисляем среднеквадратичное отклонение (относительное) по формуле:
Разработка неформальных математических моделей Для некоторых объектов формальная математическая модель нежелательна, в таких случаях надо использовать фундаментальные закономерности, лежащие в основе процессов в данном объекте, а также умение анализировать, обобщать и т.д. Если удаётся построить неформальную математическую модель, то она 1)обеспечивает сходство реакций модели с реакцией объекта, 2)легко адаптируется при перестройке объекта, 3)а также эта ММ работает в более широком диапазоне вариаций входных и выходных параметров, чем диапазон вариаций в процессе эксперимента. В связи с этим такие модели считаются более качественными. Рассмотрим пример построения неформальной математической модели с использованием теоретико-физического подхода для аппарата-смесителя, который является частью технологической линии в производстве цемента. Этот аппарат нужен, чтобы делать однородную смесь с заданным процентным содержанием компонент.
Рис. 3.4.1. Схема аппарата–смесителя.
Сырьё: измельчённый продукт, содержащий такие основные компоненты как: окись кальция (СаО), двуокись кремния (SiO2), окись алюминия (AL2O3). В данном аппарате измельчённое сырьё интенсивно перемешивается и поступает на выход, причём для стационарного процесса имеет место материальный баланс, т.е. объем сырья на входе в единицу времени равен объему продукта на выходе в единицу времени. Поскольку относительное или процентное содержание каждого компонента может меняться во входном потоке, то оно меняется и в выходном. Для получения качественного цемента надо уметь прогнозировать относительное содержание компонент в выходном потоке от относительного содержания этих компонент во входном потоке. Следовательно, нужно найти математическую модель:
где Рассмотрим, как строиться математическая модель. Введем обозначения: 1) 2) Свх, Свых – абсолютное количество окиси кальция в объеме материалов входного и выходного потоков; 3) Rвх,Rвых – скорость потока материалов на входе и выходе; 4) V – объём смесителя; 5) DСсм – абсолютное изменение количества окиси кальция в самом смесителе за время rt; 6) Используя соотношения материального баланса и считая, что в течении достаточно малого времени
Свых = Отсюда абсолютное изменение содержания окиси кальция в смесителе. DСcм=Свх – Cвых=( С другой стороны изменение относительного процентного содержания СаО в смесителе составляет:
отсюда, DСcм= Подставляя (5) в (3), получаем:
В связи с тем, что имеет место интенсивное перемешивание измельчённой массы, то состав этой воздушно-пылевой смеси практически одинаков во всем объеме и в том числе с составом в выходном потоке и, следовательно, такое допущение (DСсм»DСвых) правомерно. Поэтому уравнение (6) можно записать в виде:
Если последнее уравнение записать в виде:
то, устремляя Dt→0, получим:
Рассуждая аналогично, можно получить уравнения, связывающие относительные содержания компонент SiO2 и Al2O3 во входном и выходном потоках:
Таким образом, построена неформальная математическая модель объекта. На основании получившегося уравнения покажем, как связаны обычные дифференциальные уравнения 1-го порядка Решение дифференциального уравнения 1-го порядка с постоянными коэффициентами найдём методом разделения переменных, полагая, что х=х0
Т. к. х=х0=const, то dy»d(y–x0). Действительно: D(y–x0)=(y1–x0)|t1–(y–x0)|t2=Dy|Dt, поэтому можно записать: Проинтегрировав левую и правую части уравнения, получаем: ln(y–x0) = –wt. Подставляя пределы, получаем: ln(y–x0)–ln(yo–xo) = –w·(t–t0) или ln((y–x0)/(y0–x0))= –w·(t–t0). Потенцируем левую и правую часть:
Выполняя алгебраические преобразования, находим:
Для установления связи данного уравнения с разностным уравнением, запишем данное уравнение для определенных значений выходных координат в моменты t0,t1,…tn сдвинутые друг относительно друга на Dt. Обозначим эти значения функции y1,y2,…yi. Для Dt=const имеем: 1) Для 2) Для Если обозначить
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-03-02; просмотров: 118; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.116.142 (0.01 с.) |




 ,
,  - текущий номер такта решётчатой функции, ∆t – интервал квантования по времени или период дискретизации.
- текущий номер такта решётчатой функции, ∆t – интервал квантования по времени или период дискретизации.
 и являются аналогом ДУ:
и являются аналогом ДУ: 
 - это и есть разность 1-го порядка,
- это и есть разность 1-го порядка, ,
,  – период дискретизации, одинаковый во всем диапазоне исследования.
– период дискретизации, одинаковый во всем диапазоне исследования. (Метод Калмана).
(Метод Калмана).

 (разности 1-го порядка).
(разности 1-го порядка).

 .
.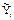 ,
, - расчетные значения выходных координат в
- расчетные значения выходных координат в  -ый момент времени,
-ый момент времени, - экспериментальные данные.
- экспериментальные данные. =A0X0+B0Y0
=A0X0+B0Y0
 =A0X1+B0Y1
=A0X1+B0Y1
 =A0Xi-1+B0Yi-1
=A0Xi-1+B0Yi-1
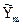 =A0Xm-1+B0Ym-1
=A0Xm-1+B0Ym-1
 , но для этого нужно знать значения A0 и B0.
, но для этого нужно знать значения A0 и B0. =A0Xi-1+B0Yi-1 вводится так называемая функция ошибки L и ставится задача нахождения значений А0 и В0 при котором L® min:
=A0Xi-1+B0Yi-1 вводится так называемая функция ошибки L и ставится задача нахождения значений А0 и В0 при котором L® min:

 ;
; 



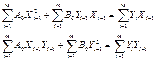




 =
=  ·
·  –(
–(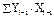 )(
)( );
); ;
; =
=  ;
; .
.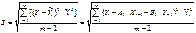
 , то нет смысла выбирать модель на основе разностного уравнения 2-го порядка, а можно оставить модель 1-го порядка. Если указанные оценки дают отрицательный результат, то переходим к следующему этапу.
, то нет смысла выбирать модель на основе разностного уравнения 2-го порядка, а можно оставить модель 1-го порядка. Если указанные оценки дают отрицательный результат, то переходим к следующему этапу.
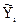 =A0Xi-1+A1Xi-2+B0Yi-1+B1Yi-2
=A0Xi-1+A1Xi-2+B0Yi-1+B1Yi-2

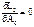 ;
;  ;
;  ;
; 


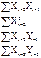


 =…
=…
 ; S2£Sдоп.
; S2£Sдоп.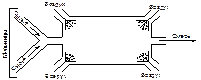
 ;
; - относительное содержание соответствующего компонента в выходном и во входном потоках.
- относительное содержание соответствующего компонента в выходном и во входном потоках. – относительное (процентное) содержание окиси кальция в объёме материалов во входных и выходных потоках;
– относительное (процентное) содержание окиси кальция в объёме материалов во входных и выходных потоках;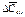 - относительное изменение содержания окиси кальция в смесителе за время rt.
- относительное изменение содержания окиси кальция в смесителе за время rt. параметры не меняются, можно записать формулы определения абсолютного содержания окиси кальция в входном и выходном потоках за время
параметры не меняются, можно записать формулы определения абсолютного содержания окиси кальция в входном и выходном потоках за время  :
: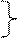 Свх =
Свх =  ·R·Dt (1)
·R·Dt (1) ·R·Dt (2)
·R·Dt (2) –
–  )·R·Dt (3)
)·R·Dt (3)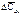 =DСсм/V (4)
=DСсм/V (4)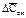 · V (5)
· V (5) ·V=(
·V=( –
–  )·R·Dt (6)
)·R·Dt (6) = (R/V)·(
= (R/V)·( –
– 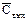 )·Dt (7)
)·Dt (7) /Dt=(R/V)·(
/Dt=(R/V)·( –
–  ), и обозначать (R/V)=w,
), и обозначать (R/V)=w,


 с разностным уравнением вида yi=A0·xi-1+B0·yi-1
с разностным уравнением вида yi=A0·xi-1+B0·yi-1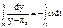

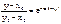 или
или 
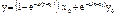 – решение исходного дифференциального уравнения.
– решение исходного дифференциального уравнения. :
: 
 :
: 
 ;
;  то последнее выражение можно записать в виде: yi=A0·хi-1+B0·yi-1. Это и есть разностное уравнение 1-го порядка. Отсюда видно, что разностное уравнение может быть получено из решения дифференциального уравнения. При этом значения коэффициентов разностного уравнения зависят от коэффициентов дифференциального уравнения и периода дискретизации Dt.
то последнее выражение можно записать в виде: yi=A0·хi-1+B0·yi-1. Это и есть разностное уравнение 1-го порядка. Отсюда видно, что разностное уравнение может быть получено из решения дифференциального уравнения. При этом значения коэффициентов разностного уравнения зависят от коэффициентов дифференциального уравнения и периода дискретизации Dt.


