
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверка гипотезы о значимости коэффициента корреляцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Выборочный коэффициент корреляции rв является точечной оценкой коэффициента корреляции r. Равенство rв =0 еще не свидетельствует о том, что r =0, а следовательно, о некоррелированности случайных величин Х и Y. Чтобы выяснить, находятся ли случайные величины в корреляционной зависимости, нужно проверить значимость выборочного коэффициента корреляции, т.е. установить, достаточна ли его величина для обоснования вывода о наличии корреляционной связи. Для этого проверяют нулевую гипотезу Н0: r= 0. Объем выборки может быть любым. Вычисляют статистику
которая имеет распределение Стьюдента с k=n- 2степенями свободы. Для проверки нулевой гипотезы по уровню значимости Если
ПРИМЕР По заданной выборке: 1) оценить тесноту линейной связи, вычислив выборочный коэффициент корреляции; 2) проверить гипотезу о значимости коэффициента корреляции при уровне значимости 0,05.
РЕШЕНИЕ Для решения задачи составим таблицу 1. Таблица 1
2) Выборочный коэффициент корреляции вычислим по формуле
По значению коэффициента корреляции
2) Выдвинем нулевую гипотезу Н0:r= 0. По формуле
По числу степеней свободы k= 11-2=9 и уровню значимости
Задание По заданной выборке: 1) оценить тесноту линейной связи, вычислив выборочный коэффициент корреляции двумя способами: а) с помощью таблицы Excel или «вручную» и б) проверьте свои расчеты с помощью статистической функции КОРРЕЛ мастера функций fx пакета Excel; 2) проверить гипотезу о значимости коэффициента корреляции при уровне значимости 0,05.
ВАРИАНТ 1
ВАРИАНТ 2
ВАРИАНТ 3
ВАРИАНТ 4
ВАРИАНТ 5
ВАРИАНТ 6
ВАРИАНТ 7
ВАРИАНТ 8
ВАРИАНТ 9
ВАРИАНТ 10
Таблица 2 - Критические точки распределения Стьюдента
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2019-04-27; просмотров: 4657; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.23.38 (0.006 с.) |

 ,
,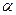 и числу степеней свободы k находят по таблице распределения Стьюдента (t- распределение, табл. Приложения 6) критическое значение
и числу степеней свободы k находят по таблице распределения Стьюдента (t- распределение, табл. Приложения 6) критическое значение  , удовлетворяющее условию
, удовлетворяющее условию  .
. , то нулевую гипотезу об отсутствии корреляционной связи между величинами Х и Y следует отвергнуть. Переменные считают зависимыми. При
, то нулевую гипотезу об отсутствии корреляционной связи между величинами Х и Y следует отвергнуть. Переменные считают зависимыми. При  нет оснований отвергать нулевую гипотезу.
нет оснований отвергать нулевую гипотезу.
 , также используя данные таблицы 1:
, также используя данные таблицы 1: .
. можно сделать вывод о том, что между величинами Х и Y существует заметная линейная корреляционная связь.
можно сделать вывод о том, что между величинами Х и Y существует заметная линейная корреляционная связь. .
. из таблицы 2 (в конце работы) находим
из таблицы 2 (в конце работы) находим 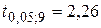 . Так как
. Так как  , то нулевую гипотезу отвергаем. Переменные Х и Y зависимы.
, то нулевую гипотезу отвергаем. Переменные Х и Y зависимы. (двусторонняя критическая область)
(двусторонняя критическая область)




