
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Комбинаторные правила произведения и суммыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Практическое занятие №1-2 Элементы комбинаторики
Комбинаторные правила произведения и суммы 1. Каждую секунду точка М передвигается по координатной плоскости на 1 вправо или на 1 вверх. Стартует точка М из начала координат. Сколько существует различных траекторий движения точки М за 5 секунд? 2. Города А и В соединяются двумя шоссейными дорогами, которые пересечены десятью проселочными. Сколькими разными способами можно добраться от А до В, чтобы ни разу не пересекать пройденный путь? 3. Сколько разных трехзначных чисел можно составить из цифр 1, 2, 3, 4 и 5 при условии, что ни одна цифра не повторяется? 4. У одного человека имеется 8 книг, а у другого – 9. Сколькими способами они могут обменять друг у друга книгу на книгу? 5. В вагоне 10 пассажиров. Поезд останавливается на 15 станциях. Сколькими способами пассажиры могут выйти из вагона? 6. Четверо учеников сдают экзамен. Сколькими способами могут быть поставлены им оценки, если известно, что никому из них не будет поставлена неудовлетворительная оценка? Перестановки 1. Сколькими способами можно расставить на книжной полке библиотеки 5 книг по математике, 3 книги по литературе и 2 книги по истории, если книги по каждому предмету одинаковые? 2. У мамы 2 яблока, 3 груши и 4 апельсина. Каждый день в течение девяти дней она выдает сыну по одному фрукту. Сколькими способами это может быть сделано? 3. Найти сумму всех четырехзначных чисел, которые получаются при перестановке цифр 2, 3, 5, 6. 4. В течение десяти недель школьники должны написать 10 контрольных работ, в том числе 2 по математике. Сколькими способами можно составить расписание этих работ так, чтобы контрольные работы по математике не шли друг за другом? 5. Сколькими способами можно расставить белые фигуры (2 ладьи, 2 слона, 2 коня, ферзь и король) на первой линии шахматной доски? 6. Рассмотрим всевозможные натуральные семизначные числа, в десятичной записи которых по одному разу используются цифры 1, 2, 3, 4, 5, 6, 7. Пронумеруем эти числа в порядке возрастания. Какое число будет иметь номер 1995? Выборки 1. Сколькими способами можно рассадить 4 учащихся на 25 местах? 2. Сколько словарей надо издать, чтобы можно было непосредственно выполнять переводы с любого из пяти языков: русского, английского, немецкого, французского, итальянского, на любой другой из этих пяти языков? 3. На плоскости даны 10 точек, причем никакие три из них не лежат на одной прямой. Сколько различных прямых можно провести через данные точки? 4. Из 20 участников собрания надо выбрать председателя и секретаря. Сколькими способами можно это сделать? 5. Из 20 учащихся надо выбрать двух дежурных. Сколькими способами это можно сделать? 6. На странице альбома 6 свободных мест для фотографий. Сколькими способами можно вложить в свободные места: а) 2 фотографии; б) 4 фотографии; в) 6 фотографий? 7. На плоскости отметили 5 точек. Их надо обозначить латинскими буквами. Сколькими способами это можно сделать (в латинском алфавите 26 букв)? 8. На школьном вечере присутствуют 12 девушек и 15 юношей. Сколькими способами можно выбрать из них 4 пары для танца? 9. Имеется неограниченное число монет по 1, 5 и 10 копеек. Сколькими способами можно образовать набор из 20 монет? 10. 20 различных деталей раскладывают в три ящика, причем в первый ящик кладут три детали, во второй – 5 деталей, а в третий – все остальные детали. Сколькими способами это можно сделать? 11. В колоде 36 карт. Раздаются 3 карты. Сколько может быть случаев появления одного туза среди розданных карт? 13. В одном сказочном государстве не найдется двух человек с одинаковым составом зубов: либо у них разное число зубов, либо зубов нет в разных местах. Оцените наибольшую численность населения в этом государстве, если максимальное число зубов у одного человека 32. 14. В лаборатории работают 8 физиков и 10 химиков. В рабочую группу по теме исследования должны войти 2 физика и 3 химика. Сколькими способами можно составить рабочую группу? 15. Сколькими способами можно добраться из точки А в точку В, если идти только вправо и вверх?
Практическое занятие № 2-3 Практическое занятие № 4 Операции над вероятностями 1. В экзаменационные билеты включено по два теоретических вопроса и одна задача. Всего составлено 28 билетов, содержащих разные вопросы и задачи. Студент подготовил только 50 теоретических вопросов и сможет решить задачи к 22-м билетам. Какова вероятность того, что вынув наудачу билет, студент ответит на все вопросы? 2. Два охотника стреляют в волка, причем каждый делает по одному выстрелу. Для первого охотника вероятность попадания в цель 0,7, для второго – 0,8. Какова вероятность попадания в волка? 3. В коробке имеется 2 красных, 3 синих и 2 зеленых карандаша. Из нее наудачу без возвращения вынимают один за другим по одному карандашу. Найти вероятность того, что красный карандаш появится раньше синего. 4. Как известно, чтобы предотвратить расхищение сокровищ из пирамид, египтяне создавали в них лабиринты; двигаясь по ним случайно, похитители зачастую гибли в ямах-ловушках. 1. Чему равна вероятность того, что кладоискатель найдет клад, и вероятность того, что он погибнет (для рис. 2 и 3)? 2. Чему равны эти вероятности для лабиринта рис.10 при условии, что кладоискатель может бродить случайно сколь угодно долго и делать петли?
5. В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. Сегодня 3 июля, погода в Волшебной стране хорошая. Найдите вероятность того, что 6 июля в Волшебной стране будет отличная погода. 6. Чтобы поступить в институт на специальность «Лингвистика», абитуриент должен набрать на ЕГЭ не менее 64 баллов по каждому из трёх предметов — математика, русский язык и иностранный язык. Чтобы поступить на специальность «Социология», нужно набрать не менее 64 баллов по каждому из трёх предметов — математика, русский язык и обществознание. Вероятность того, что абитуриент Б. получит не менее 64 баллов по математике, равна 0,5, по русскому языку — 0,9, по иностранному языку — 0,8 и по обществознанию — 0,9. Найдите вероятность того, что Б. сможет поступить: а) на одну из двух упомянутых специальностей; б) хотя бы на одну из двух упомянутых специальностей. 7. Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 4 очка в двух играх. Если команда выигрывает, она получает 3 очка, в случае ничьей — 1 очко, если проигрывает — 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,4. 8. Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ выявляет гепатит, то результат анализа называется положительным. У больных гепатитом пациентов анализ даёт положительный результат с вероятностью 0,9. Если пациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью 0,01. Известно, что 5% пациентов, поступающих с подозрением на гепатит, действительно больны гепатитом. Найдите вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным. 9. Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,02. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,99. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,01. Найдите вероятность того, что случайно выбранная из упаковки батарейка будет забракована. 10. При переливании крови надо учитывать группу крови донора и больного. Имеющему четвертую группу крови можно переливать кровь любой группы, человеку со второй и третьей можно переливать кровь той же группы и первой, человеку с первой группой крови можно переливать кровь только первой группы. Среди населения 33,7% имеют первую группу, 37,5% - вторую, 20,9% - третью и 7,9% - четвертую группу крови. Найти вероятность того, что случайно взятому больному можно перелить кровь случайно взятого донора. Лабораторная работа №1 Вариант 1 Задание 1 Проводится серия из 10 испытаний. В каждом из них вероятность появления события А постоянна и равна 0,3. Определить с помощью функции БИНОМ.РАСП мастера функций fx пакета Excelвероятность того, что событие А появится 7 раз; не более 5 раз. Задание 2 Ученик не подготовился к тесту и поэтому отвечает на вопросы теста наугад. Составьте ряд распределения числа правильных ответов, если тест состоит из 7 вопросов, к каждому вопросу дается 4 ответа, причем только один из них верный. Всевозможные вероятности вычислите с помощью функции БИНОМ.РАСП мастера функций fx пакета Excel. Задание 3 Ученик не подготовился к тесту и поэтому отвечает на вопросы теста наугад. Начиная с какого числа правильных ответов, ученику можно ставить положительную оценку? Заполните таблицу, если тест состоит из п вопросов, к каждому вопросу дается т ответов, причем только t из них верных:
Для вычислений используйте функцию БИНОМ.РАСП мастера функций fx пакета Excel.
Вариант 2 Задание 1 Проводится серия из 11 испытаний. В каждом из них вероятность появления события А постоянна и равна 0,4. Определить с помощью функции БИНОМ.РАСП мастера функций fx пакета Excel вероятность того, что событие А появится 7 раз; не более 5 раз. Задание 2 Ученик не подготовился к тесту и поэтому отвечает на вопросы теста наугад. Составьте ряд распределения числа правильных ответов, если тест состоит из 8 вопросов, к каждому вопросу дается 3 ответа, причем только один из них верный. Всевозможные вероятности вычислите с помощью функции БИНОМ.РАСП мастера функций fx пакета Excel. Задание 3 См. задание 3 варианта 1. Вариант 3 Задание 1 Проводится серия из 10 испытаний. В каждом из них вероятность появления события А постоянна и равна 0,2. Определить с помощью функции БИНОМ.РАСП мастера функций fx пакета Excelвероятность того, что событие А появится 5 раз; не более 3 раз. Задание 2 Ученик не подготовился к тесту и поэтому отвечает на вопросы теста наугад. Составьте ряд распределения числа правильных ответов, если тест состоит из 10 вопросов, к каждому вопросу дается 5 ответов, причем только один из них верный. Всевозможные вероятности вычислите с помощью функции БИНОМ.РАСП мастера функций fx пакета Excel. Задание 3 См. задание 3 варианта 1. Лабораторная работа №2 «Описательная статистика» Статистические функции СЧЕТ, МОДА, МЕДИАНА, СРЗНАЧ, ДИСПР, ДИСП, СТАНДОТКЛОНП, СКОС и ЭКСЦЕСС мастера функций fx пакета Excel позволяют определить для выборки объем, моду, медиану, выборочное среднее, выборочную дисперсию, исправленную выборочную дисперсию, выборочное стандартное отклонение, асимметрию и эксцесс соответственно. А вот надстройка Пакет анализа позволяет получить сразу все характеристики выборки. Для доступа к этим инструментам нажмите кнопку Анализ данных в группе Анализ на вкладке Данные. Данные Появится окно:
Если кнопка Анализ данных недоступна, необходимо загрузить надстройку "Пакет анализа". Для этого: 1. На вкладке Файл выберите команду Параметры, а затем — категорию Надстройки. 2. В списке Управление выберите пункт Надстройки Excel и нажмите кнопку Перейти. 3. В окне Доступные надстройки установите флажок Пакет анализа и нажмите кнопку ОК. Если пункт Пакет анализа отсутствует в списке Доступные надстройки, нажмите кнопку Обзор, чтобы найти надстройку. Если выводится сообщение о том, что надстройка "Пакет анализа" не установлена на компьютере, нажмите кнопку Да для ее установки. Пример 1. Для выборки 2, 3, 5, 6, 7, 9, 6, 3, 4, 5, 6, 7, 4, 2, 1 определим с помощью Excel характеристики выборки. Введем в ячейки А1:А15 наши данные. Данные (Сервис Появится диалоговое окно, которое нужно заполнить:
После нажатия кнопки Ок получаем итоговую таблицу:
Пример 2. Результаты экзамена по математическому анализу представлены в таблице:
Построим в документе Microsoft Word с помощью мастера диаграмм пакета Excel столбчатую и круговую диаграммы, а также полигон частот. Вставка
После этого раскроется диалоговое окно Excel с некоторыми данными в ячейках и появится соответствующая этим данным гистограмма. Внесем изменения в ячейках А1:В5 в соответствии с данными нашего примера, остальные данные удалим:
Одновременно с изменениями в ячейках будет изменяться информация на гистограмме.
Теперь можно изменить название гистограммы и подписи осей. Выделив поле названия, заменим надпись «число студентов» на результаты экзамена». Чтобы изменить подписи горизонтальной оси, нажмем правой кнопкой мышки на область диаграммы, в открывшейся вкладке выберем команду «Изменить данные».
Нажмем правой кнопкой мышки на область диаграммы, в открывшейся вкладке выберем команду «Изменить тип диаграммы», заменив гистограмму на круговую диаграмму.
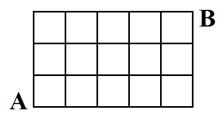
Задание 1. Для выборки 3, 4, 5, 6, 9, 7, 2, 1, 4, 5, 7, 8, 4, 7 определить с помощью Excel характеристики выборки. Задание 2 В таблице приведены размеры одежды 50 учащихся 9 класса: На основании этих данных составить таблицу распределения по частотам значений случайной величины 1) Построить полигон частот. 2) Найти среднее значение величины Задание 3 При изучении учебной нагрузки учащихся попросили 32 восьмиклассников отметить время (с точностью до 0,1 ч), которое они затратили в определенный день на выполнение домашних заданий. Получили следующие данные:
Представьте полученные данные в виде интервального ряда с интервалами длиной 0.5 ч. Найдите среднее время, потраченное на выполнение домашних заданий. Постройте полигон частот. Задание 4 Гистограмма характеризует распределение призывников по росту:
А) число призывников ростом от 180 до 185 см; Б) группу роста, к которой относится наибольшее число призывников; В) общее число призывников; Для случайной величины Лабораторная работа №3 «Критерий Крамера-Уэлча» Задание 1 В двух группах учащихся — экспериментальной и контрольной — получены следующие результаты по учебному предмету (тестовые баллы; см. табл.). Результаты эксперимента
Выдвинем гипотезы: Н0: средние тестовые баллы по учебному предмету в экспериментальной и контрольной группах совпадают. Н1: средние тестовые баллы по учебному предмету в экспериментальной и контрольной группах не совпадают. Проверьте нулевую гипотезу с помощью критерия Крамера-Уэлча, подсчитав следующие характеристики:
Если
Пример. Время на производство одной детали по первой технологии (с): 27, 28, 29, 27, 28, 29, 31, 32, 30, 29. Время на производство одной детали по второй технологии (с): 28, 29, 27, 28, 29, 32, 31, 33. Доверительная вероятность 95%. Можно ли сделать вывод, что время на производство одной детали в этих технологиях различается? Выдвинем гипотезы: Н0: время на производство одной детали в этих технологиях одинаково. Н1: время на производство одной детали в этих технологиях различается. Укажем время на производство одной детали в ячейках А1:А11 и В1:В9:
Сначала надо выяснить, различаются ли в технологиях 1 и 2 неизвестные дисперсии. Данные Откроется диалоговое окно, которое нужно заполнить:
В графе Интервал переменной 1 указывается ссылка на ячейки, содержащие значения первой выборки. В графе Интервал переменной 2 указывается ссылка на ячейки, содержащие значения второй выборки. В графе альфа указывается уровень значимости
При нажатии кнопки Ок откроется итоговое окно:
Так как в графе P(F<=f) одностороннее указано величина, большая выбранного Альфа (0,223150144>0,05), то принимаем заключение о том, что неизвестные дисперсии не различаются. Воспользуемся двухвыборочным t- тестом с одинаковыми дисперсиями. Вернемся на Лист 1. Данные Заполняем раскрывшееся диалоговое окно:
На новом рабочем листе откроется итоговое окно:
Так как Р(Т<=t) двухстороннее больше заданного альфа, то гипотеза Н0 принимается на уровне значимости 0,05. Время на производство одной детали в этих технологиях одинаково. Замечание. Если Двухвыборочный F-тест для дисперсии покажет различие дисперсий (в графе P(F<=f) одностороннее указано величина, меньшая выбранного Альфа), то необходимо воспользоваться двухвыборочным t- тестом с различными дисперсиями. Данные Задание 2 Выполните задание 1 по алгоритму, рассмотренному в примере. Лабораторная работа №4 «Критерий знаков G» Число ошибок, допущенных учащимися при выполнении однотипных тестовых заданий до объяснения учителя и после представлены в таблице. Выдвинем гипотезы: Н0: сдвиг в отрицательную (типичную) сторону является случайным (т.е. объяснение материала учителем не было эффективным). Н1: сдвиг в отрицательную (типичную) сторону не является случайным (т.е. объяснение материала учителем было эффективным). Проверьте нулевую гипотезу с помощью критерия знаков. Нулевые сдвиги отбрасываются; количество ненулевых сдвигов: Типичные сдвиги те, которых больше. Значение Если Если При различных значениях ненулевых сдвигов критическое значение
Вариант 1
Нулевые сдвиги отбрасываются; количество ненулевых сдвигов: Вариант 2
Нулевые сдвиги отбрасываются; количество ненулевых сдвигов: Вариант 3
Нулевые сдвиги отбрасываются; количество ненулевых сдвигов: Лабораторная работа №5 «Критерий χ2 (хи-квадрат)»
Критерий χ2 (хи-квадрат) применяется в двух целях: 1) для сопоставления эмпирического распределения признака с теоретическим – равномерным, нормальным или каким-то иным, 2) для сравнения распределений объектов двух совокупностей на основе измерений по шкале наименований в двух независимых выборках (критерий однородности χ2).
Критерий не рекомендуется использовать, если: 1) 2) хотя бы одна из абсолютных частот в таблице, составленной на основе экспериментальных данных, меньше 5.
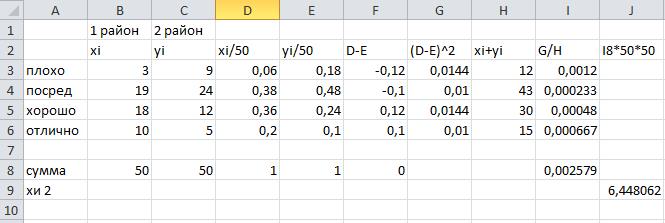
Задача 1. Проводился эксперимент, направленный на выявление лучшего из учебников, написанных двумя авторскими коллективами в соответствии с целями обучения геометрии и содержанием программы IX класса. Для проведения эксперимента методом случайного отбора были выбраны два района, большинство школ которых относились по расположению к сельским. Учащиеся первого района (20 классов) обучались по учебнику № 1, учащиеся второго района (15 классов) обучались по учебнику №2. Методом случайного отбора из учащихся первого района, писавших проверочную работу, была составлена выборка объемом 50 человек, из учащихся второго района — выборка объемом 50 человек. В соответствии со специально разработанными критериями оценки выполнения работы каждый ученик мог попасть в одну из четырех категорий: плохо, посредственно, хорошо, отлично. Результаты выполнения работы двумя выборками учащихся используем для проверки гипотезы о том, что учебник № 1 способствует лучшему усвоению проверяемого раздела курса, т. е. учащиеся первого экспериментального района в среднем будут получать более высокие оценки, чем учащиеся второго района. Результаты выполнения работы учащимися обеих выборок представлены в виде таблицы:
Выдвинем гипотезу:
Используя критерий χ2 проверьте нулевую гипотезу при уровне значимости 0,05 и сделайте выводы. χ2набл. Если χ2набл.
Критические значения χ2кр. при уровне значимости 0,05 находятся по таблице:
Задача 2. Проверьте свои расчеты с помощью таблицы Excel. Примерный образец представлен на рисунке.
Задача 3. В экспериментальной группе учащихся проверялась одна из методик изучения нового материала. Для выявления эффективности методики была выделена контрольная группа учащихся, которая изучала новый материал по традиционной методике. Данные представлены в таблице:
Проверьте при уровне значимости 0,05 гипотезы: 1) 2) 3) Рассмотрим применение критерия χ2 для сопоставления эмпирического распределения признака с теоретическим. Задача 4 (пример приведен из книги Е.Сидоренко «Методы математической обработки в психологии»). В комедии Н.В. Гоголя «Женитьба» у купеческой дочери Агафьи Тихоновны было пять женихов. Одного она сразу исключила из рассмотрения, потому что он был купеческого звания, как и она сама. А из остальных не знала, кого выбрать. Ей хотелось, чтобы жених совмещал в себе достоинства всех четверых. Но поскольку вывести среднюю величину из четверых людей невозможно, то Агафья Тихоновна была в смятении. Допустим, её тетушка или сваха за полчаса смотрин зафиксировали следующие наблюдения. Агафья Тихоновна: Сидела с опущенными глазами 25 минут; Благосклонно смотрела на Никанора Ивановича 14 раз; Благосклонно смотрела на Ивана Кузьмича 5 раз; Благосклонно смотрела на Ивана Павловича 8 раз; Благосклонно смотрела на Балтазара Балтазарыча 5 раз. (Все приведенные эмпирические частоты на самом деле пропорциональны количеству благосклонных высказываний невесты о женихах в тексте пьесы.) Представьте данные в виде таблицы:
Если Агафья Тихоновна никому не отдает предпочтения, то данное распределение направленности её взгляда не будет отличаться от равномерного: она на всех смотрит с одинаковой частотой. Но если достоинства одного из женихов чаще притяг
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2019-04-27; просмотров: 1029; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.148.203 (0.017 с.) |


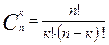
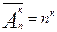



 п1+п2+…+пк=п
п1+п2+…+пк=п


 Анализ данных
Анализ данных 








 - размеров одежды учащихся 9 класса.
- размеров одежды учащихся 9 класса. Пользуясь гистограммой, найдите:
Пользуясь гистограммой, найдите: , где
, где  ,
,  ,
,  .
. , то нулевая гипотеза отвергается.
, то нулевая гипотеза отвергается.

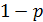 . В нашем случае это 0,05. Также указываются параметры вывода (выходной интервал, новый рабочий лист, новая рабочая книга).
. В нашем случае это 0,05. Также указываются параметры вывода (выходной интервал, новый рабочий лист, новая рабочая книга).



 .
. - количество нетипичных сдвигов.
- количество нетипичных сдвигов. , то нулевая гипотеза отклоняется, принимается конкурирующая гипотеза.
, то нулевая гипотеза отклоняется, принимается конкурирующая гипотеза. , то критерий знаков неприменим.
, то критерий знаков неприменим. при уровне значимости р<0,05 находят из таблицы:
при уровне значимости р<0,05 находят из таблицы: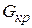
 .
. .
. .
. ,
,  (в одних источниках);
(в одних источниках);  (в других источниках);
(в других источниках); : учебник № 1 не способствует лучшему усвоению проверяемого раздела курса.
: учебник № 1 не способствует лучшему усвоению проверяемого раздела курса. .
.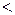 χ2кр., то нет оснований отвергнуть нулевую гипотезу.
χ2кр., то нет оснований отвергнуть нулевую гипотезу.
 : в экспериментальной группе не произошло существенных изменений в распределении учащихся по уровню знаний после применения новой методики (т.е. новая методика не дала эффекта).
: в экспериментальной группе не произошло существенных изменений в распределении учащихся по уровню знаний после применения новой методики (т.е. новая методика не дала эффекта).


